Pole podstawy walca jest równe 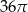 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
A) 3 B) 6 C) 9 D) 18
/Szkoła podstawowa/Zadania testowe
Rozwiązaniem równania 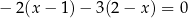 jest liczba
jest liczba
A) 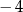 B)
B) 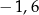 C) 0,8 D) 4 E) 8
C) 0,8 D) 4 E) 8
Rozwiązaniem równania 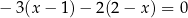 jest liczba
jest liczba
A) 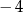 B)
B) 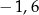 C)
C) 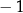 D) 4 E) 8
D) 4 E) 8
Prostokąt podzielono na dwa identyczne trapezy równoramienne i dwa trójkąty w sposób pokazany na rysunku.
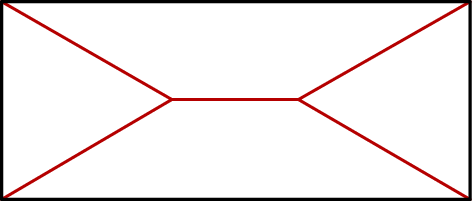
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Trójkąty, które powstały w sposób pokazany na rysunku, sąrównoramienne. | P | F |
Gdyby kąty ostre trapezów miały miarę 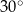 , to powstałe trójkąty byłyby równoboczne. , to powstałe trójkąty byłyby równoboczne. | P | F |
Wykres przedstawia zależność ilości farby pozostałej w pojemniku (w litrach) od powierzchni ściany (w 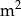 ) pomalowanej farbą z tego pojemnika.
) pomalowanej farbą z tego pojemnika.
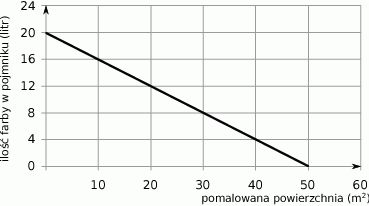
Ile farby pozostało w pojemniku po pomalowaniu 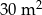 ściany?
ściany?
A) 8 litrów B) 12 litrów C) 16 litrów D) 20 litrów
Wykres przedstawia zależność ilości farby pozostałej w pojemniku (w litrach) od powierzchni ściany (w 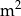 ) pomalowanej farbą z tego pojemnika.
) pomalowanej farbą z tego pojemnika.
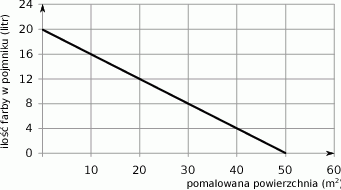
Ile farby zużyto na pomalowanie 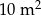 ściany?
ściany?
A) 4 litry B) 8 litrów C) 10 litrów D) 16 litrów
Liczbą przeciwną do liczby 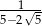 jest liczba:
jest liczba:
A) 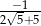 B)
B) 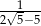 C)
C) 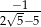 D)
D) 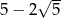
Liczbą przeciwną do liczby 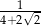 jest liczba
jest liczba
A) 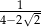 B)
B) 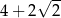 C)
C) 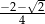 D)
D) 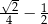
Wartość wyrażenia 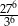 jest równa A/B.
jest równa A/B.
A) 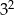 B)
B) 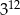
Wartość wyrażenia 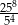 jest równa C/D.
jest równa C/D.
C) 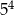 D)
D) 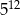
Iloraz 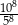 jest równy A/B.
jest równy A/B.
A) 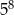 B)
B) 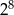
Iloczyn 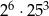 jest równy C/D.
jest równy C/D.
C) 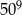 D)
D) 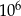
Wartość wyrażenia 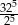 jest równa A/B.
jest równa A/B.
A) 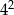 B)
B) 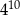
Wartość wyrażenia 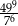 jest równa C/D.
jest równa C/D.
C) 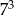 D)
D) 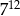
Iloraz 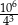 jest równy A/B.
jest równy A/B.
A) 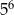 B)
B) 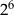
Iloczyn 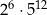 jest równy C/D.
jest równy C/D.
C) 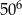 D)
D) 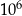
Na osi liczbowej zaznaczono sześć liczb całkowitych. Cztery z tych liczb oznaczono literami: 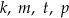 .
.

Które z poniższych wyrażeń ma wartość równą 1?
A) 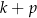 B)
B) 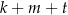 C)
C) 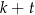 D)
D) 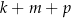
Wysokości 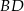 i
i 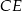 trójkąta równobocznego
trójkąta równobocznego 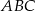 przecinają się w punkcie
przecinają się w punkcie 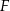 .
.
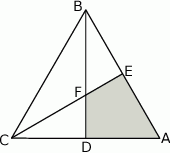
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole czworokąta 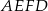 stanowi stanowi  pola trójkąta pola trójkąta 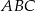 . . | P | F |
Jeden z kątów czworokąta 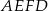 ma miarę ma miarę 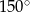 . . | P | F |
Właściciel sklepu zyskuje 12% z wartości każdej sprzedanej pary obuwia. Ile par tenisówek, których cena wynosi 80 zł, musi sprzedać, aby zyskać 2400 zł?
A) 250 B) 200 C) 240 D) 300
Tydzień przed rozpoczęciem zajęć student zapłacił 800 zł za kurs żeglarski. W razie rezygnacji z kursu organizator nie zwraca pełnej kwoty wpłaty, tylko oddaje jej część, zgodnie z poniższą tabelą.
| Termin rezygnacji | Wysokość zwrotu wpłaty |
| przed rozpoczęciem kursu | 95% |
| w pierwszym tygodniu kursu | 85% |
| w drugim tygodniu kursu | 70% |
| po upływie drugiego tygodnia | 5% |
Student zrezygnował z kursu w trzecim dniu zajęć. Organizator zwrócił studentowi kwotę
A) 120 zł B) 560 zł C) 680 zł D) 760 zł
Liczbę 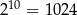 możemy przybliżyć tak:
możemy przybliżyć tak: 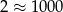 , a liczbę
, a liczbę 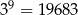 tak:
tak: 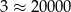 . To pozwala przybliżać inne liczby, na przykład
. To pozwala przybliżać inne liczby, na przykład 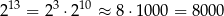 .
.
Wykorzystując podane przybliżenia liczb 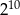 oraz
oraz 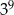 , wybierz najlepsze przybliżenie liczb
, wybierz najlepsze przybliżenie liczb 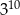 ,
, 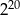 oraz
oraz 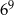 .
.
| Potęga | Propozycje przybliżeń | ||
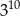 | A) 30 000 | B) 60 000 | C) 200 000 |
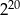 | A) 2 000 | B) 4 000 | C) 1 000 000 |
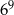 | A) 15 000 | B) 40 000 | C) 10 000 000 |
W tabeli podano, w jaki sposób zmienia się cena biletu na prom w ciągu całego roku.
| Cena podstawowa biletu na prom | 40 zł |
| Cena biletu w sezonie zimowym | cena podstawowa obniżona o 20% |
| Cena biletu w sezonie letnim | cena podstawowa podwyższona o 200% |
| Cena biletu poza sezonem zimowym i letnim | cena podstawowa |
Bilet na prom w sezonie letnim jest droższy od biletu w sezonie zimowym o
A) 88 zł B) 72 zł C) 48 zł D) 32 zł
W tabeli podano, w jaki sposób zmienia się cena biletu na górskim wyciągu linowym w ciągu całego roku.
| Cena podstawowa biletu na wyciąg | 50 zł |
| Cena biletu w sezonie zimowym | cena podstawowa podwyższona o 140% |
| Cena biletu w sezonie letnim | cena podstawowa obniżona o 30% |
| Cena biletu poza sezonem zimowym i letnim | cena podstawowa |
Bilet na wyciąg w sezonie letnim jest tańszy od biletu w sezonie zimowym o
A) 70 zł B) 15 zł C) 85 zł D) 55 zł
Jeżeli przyjmiemy, że 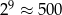 i
i 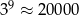 , to za przybliżenie liczby
, to za przybliżenie liczby 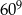 możemy przyjąć
możemy przyjąć
A) 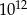 B)
B) 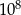 C)
C) 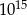 D)
D) 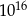
Kacper zabrał na wycieczkę dwa razy mniej pieniędzy niż Wojtek. Kacper wydał połowę swoich pieniędzy, a Wojtek wydał 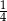 swoich.
swoich.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kacper wydał tyle samo pieniędzy, ile wydał Wojtek. | P | F |
| Po wycieczce Kacprowi zostało trzy razy mniej pieniędzy niż Wojtkowi. | P | F |
Iza rzuciła 10 razy standardową sześcienną kostką do gry. W trakcie rzutów obliczała sumę 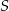 wyrzuconych oczek według następującej reguły: jeżeli liczba wyrzuconych oczek była nieparzysta, to dodawała tę liczbę do sumy
wyrzuconych oczek według następującej reguły: jeżeli liczba wyrzuconych oczek była nieparzysta, to dodawała tę liczbę do sumy 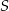 , a jeżeli liczba wyrzuconych oczek była parzysta, to odejmowała tę liczbę od
, a jeżeli liczba wyrzuconych oczek była parzysta, to odejmowała tę liczbę od 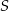 . Na diagramie przedstawiono wartości sumy
. Na diagramie przedstawiono wartości sumy 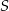 po kolejnych rzutach.
po kolejnych rzutach.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Iza cztery razy wyrzuciła parzystą liczbę oczek. | P | F |
| Iza dwa razy wyrzuciła trzy oczka. | P | F |
Figura zacieniowana na rysunku jest równoległobokiem.
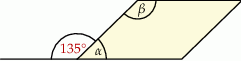
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma miar kątów  i i 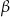 wynosi wynosi 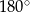 . . | P | F |
Kąt  ma miarę 3 razy mniejszą niż kąt ma miarę 3 razy mniejszą niż kąt 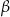 . . | P | F |
Z tasiemki o długości 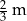 odcięto kawałek o długości pół metra. Pozostała po odcięciu część tasiemki ma długość
odcięto kawałek o długości pół metra. Pozostała po odcięciu część tasiemki ma długość
A) mniejszą od 15 cm.
B) większą od 15 cm, ale mniejszą od 16 cm.
C) równą 16 cm.
D) większą od 16 cm, ale mniejszą od 17 cm.
Makau jest jednym z najbardziej zaludnionych krajów świata, powierzchnię 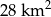 zamieszkuje 545674 ludzi. Na
zamieszkuje 545674 ludzi. Na 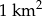 powierzchni tego kraju żyje więc średnio około
powierzchni tego kraju żyje więc średnio około
A) 20000 osób B) 15000 osób C) 10000 osób D) 2000 osób
Australia jest jednym z najsłabiej zaludnionych krajów świata powierzchnię 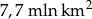 zamieszkuje 22 mln ludzi. Na
zamieszkuje 22 mln ludzi. Na 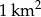 powierzchni tego kraju żyje więc średnio około
powierzchni tego kraju żyje więc średnio około
A) 1 osoba B) 2 osoby C) 3 osoby D) 30 osób
Mongolia jest jednym z najsłabiej zaludnionych krajów świata powierzchnię 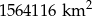 zamieszkuje 2,99 mln ludzi. Na
zamieszkuje 2,99 mln ludzi. Na 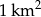 powierzchni tego kraju żyje więc średnio około
powierzchni tego kraju żyje więc średnio około
A) 0,5 osoby B) 2 osoby C) 8 osób D) 16 osób
Na loterię przygotowano 500 losów, wśród których jest 40 losów wygrywających. Każdy los wygrywający upoważnia do odbioru nagrody w wysokości 15 zł. Jak powinna być cena jednego losu, żeby przychód uzyskany ze sprzedaży wszystkich losów był wyższy od sumy wypłaconych nagród o 200 zł?
A) 1,2 zł B) 1,6 zł C) 2,6 zł D) 2,5 zł
Na loterię przygotowano 500 losów, wśród których jest 40 losów wygrywających. Każdy los wygrywający upoważnia do odbioru nagrody w wysokości 15 zł. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pierwszych 17 losów zakupionych w loterii było przegrywających. Zuzia jako 18 osoba kupuje los w tej loterii. Prawdopodobieństwo, że los Zuzi jest wygrywający jest większe niż 0,08. | P | F |
| W drugiej edycji tej loterii zwiększono liczbę losów wygrywających dwukrotnie, a liczbę losów przegrywających pozostawiono bez zmian. Zatem prawdopodobieństwo wygranej wzrosło w drugiej edycji dwukrotnie. | P | F |
Piotrek na dużej kartce w kratkę narysował figurę złożoną z 60 połączonych odcinków, które kolejno ponumerował liczbami naturalnymi od 1 do 60. Wszystkie komórki kratki są takimi samymi kwadratami. Na rysunku przedstawiono fragment tej figury, złożony z 17 początkowych odcinków. Kolejne odcinki tej figury Piotrek narysował według tej samej reguły, którą zastosował do narysowania odcinków 1–17.
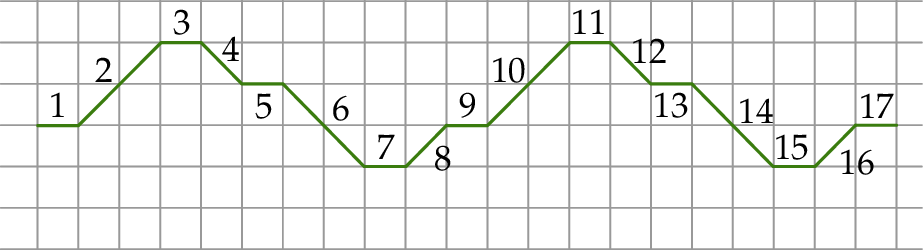
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Proste zawierające odcinki o numerach 39 oraz 53 są wzajemnie równoległe. | P | F |
| Proste zawierające odcinki o numerach 27 oraz 49 są wzajemnie prostopadłe. | P | F |

