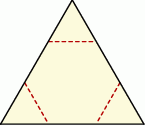
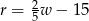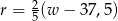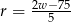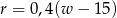Staś ma dwa jednakowe klocki w kształcie ostrosłupa prawidłowego czworokątnego, każdy o polu powierzchni całkowitej 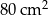 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
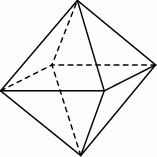
Jakie pole powierzchni ma bryła otrzymana przez Stasia?
A) 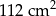 B)
B) 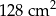 C)
C) 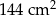 D)
D) 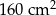

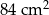 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku. 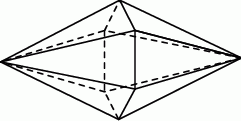
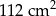

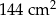
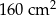
 jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,
, natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,  ,
, 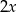 jest równa
jest równa 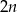 . Wynika stąd, że
. Wynika stąd, że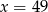
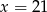
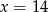
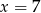
 jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,
, natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,  ,
, 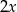 jest równa
jest równa 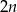 . Wynika stąd, że
. Wynika stąd, że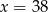
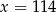
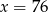
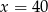
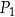 i
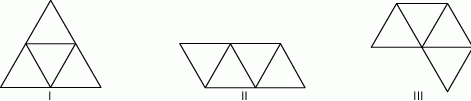
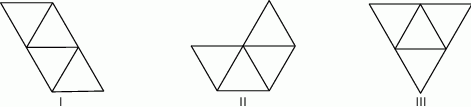
i 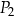 oraz podano długości ich boków.
oraz podano długości ich boków. 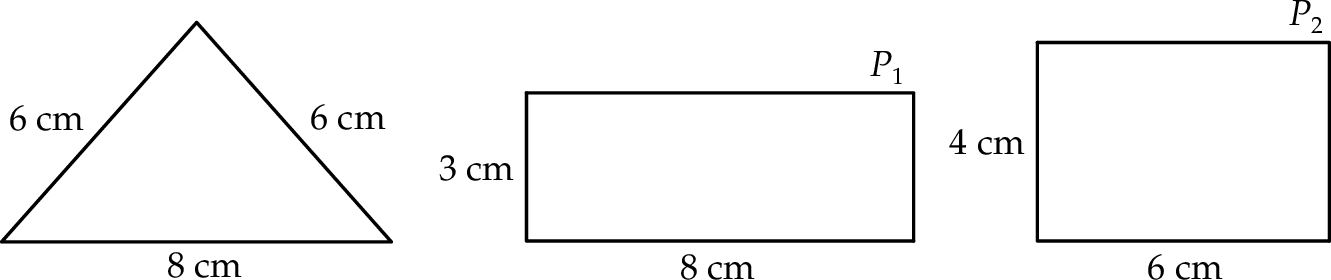
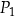 i
i 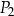 ma bok takiej samej długości jak jeden z boków trójkąta.
ma bok takiej samej długości jak jeden z boków trójkąta. 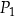 i
i 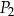 nie mają takich samych wymiarów.
nie mają takich samych wymiarów. 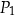 i
i 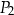 nie mają boku tej samej długości.
nie mają boku tej samej długości. 


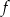 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb: 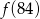 ,
, 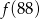 ,
, 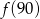 ,
, 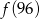 najmniejsza to
najmniejsza to 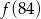
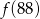
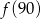
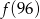
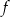 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb: 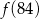 ,
, 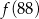 ,
, 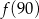 ,
, 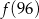 największa to
największa to 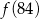
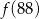
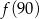
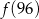
 trasy z domu do szkoły. Trasa z basenu do szkoły ma długość 800 m.
trasy z domu do szkoły. Trasa z basenu do szkoły ma długość 800 m. 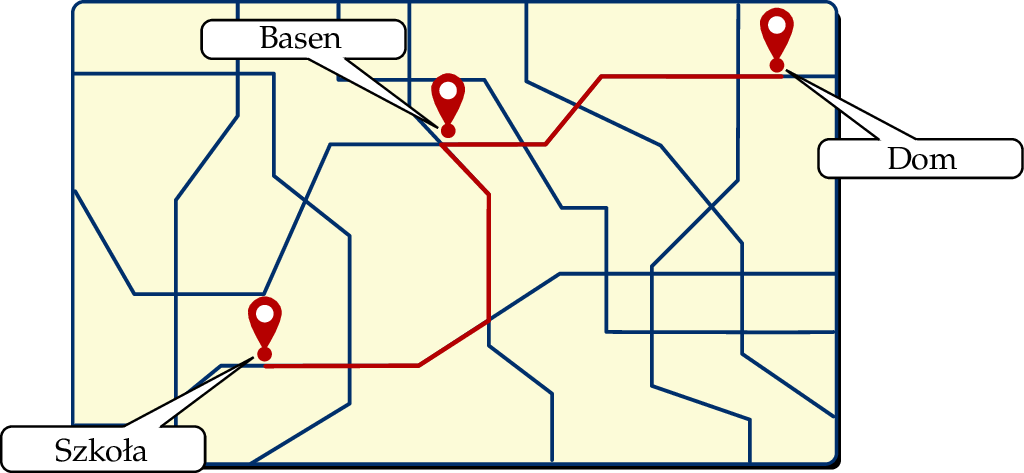
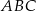 o obwodzie 34 cm poprowadzono odcinek
o obwodzie 34 cm poprowadzono odcinek 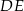 . Obwód trójkąta
. Obwód trójkąta 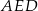 jest równy 16 cm, a obwód czworokąta
jest równy 16 cm, a obwód czworokąta 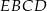 – 30 cm.
– 30 cm. 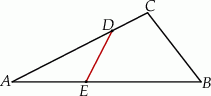
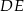 jest równa
jest równa 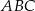 o obwodzie 128 cm poprowadzono odcinek
o obwodzie 128 cm poprowadzono odcinek 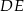 . Obwód trójkąta
. Obwód trójkąta 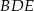 jest równy 84 cm, a obwód czworokąta
jest równy 84 cm, a obwód czworokąta 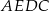 – 100 cm.
– 100 cm. 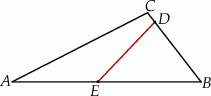
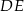 jest równa
jest równa 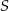 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 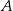 i
i 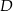 są równe
są równe 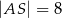 i
i 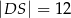 . Bok
. Bok 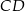 tego czworokąta ma długość
tego czworokąta ma długość 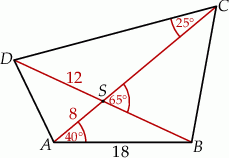
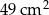 . Z wszystkich tych klocków zbudowano prostopadłościan o objętości
. Z wszystkich tych klocków zbudowano prostopadłościan o objętości 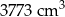 . W koszu znajdowało się A/B klocków.
. W koszu znajdowało się A/B klocków.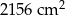
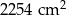
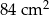 .
. 

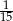
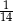
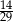
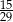
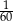
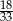
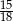
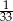
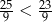
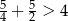
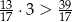
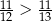
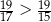
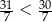
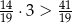
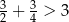
 ,
, 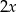 jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,
jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,  ,
,  ,
, 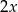 . Wynika stąd, że
. Wynika stąd, że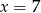
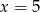
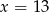
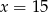
 oznacza rozmiar ramy (w cm),
oznacza rozmiar ramy (w cm), 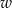 – wzrost użytkownika (też w cm).
– wzrost użytkownika (też w cm).