Dane są trzy liczby 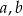 i
i  .
.
Gdy 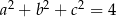 oraz
oraz  jest liczbą mniejszą od
jest liczbą mniejszą od 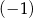 , to suma
, to suma 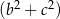 jest A/B.
jest A/B.
A) mniejsza od 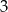 B) większa od
B) większa od 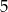
Gdy 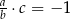 oraz
oraz 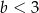 , to
, to 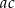 jest liczbą C/D.
jest liczbą C/D.
C) mniejszą od 3 D) większą od 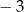
/Szkoła podstawowa/Zadania testowe
Dwie metalowe kule o promieniach po 2 cm przetopiono z kulami o promieniach 1 cm. Otrzymano jedną kulę o promieniu 3 cm. Ile łącznie kul przetopiono?
A) 11 B) 13 C) 1 D) 3
W autobusie jechało 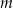 mężczyzn i
mężczyzn i 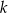 kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim
kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim
A) 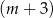 mężczyzn i
mężczyzn i 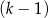 kobiet. B)
kobiet. B) 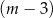 mężczyzn i
mężczyzn i 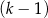 kobiet.
kobiet.
C) 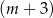 mężczyzn i
mężczyzn i 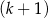 kobiet. D)
kobiet. D) 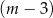 mężczyzn i
mężczyzn i 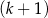 kobiet.
kobiet.
W windzie jechało 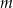 mężczyzn i
mężczyzn i 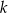 kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej
kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej
A) 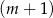 mężczyzn i
mężczyzn i 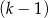 kobiet. B)
kobiet. B) 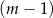 mężczyzn i
mężczyzn i 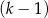 kobiet.
kobiet.
C) 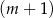 mężczyzn i
mężczyzn i 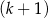 kobiet. D)
kobiet. D) 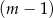 mężczyzn i
mężczyzn i 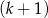 kobiet.
kobiet.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
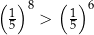 | P | F |
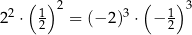 | P | F |
W pudełku jest 40 kul. Wśród nich jest 35 kul białych, a pozostałe to kule czerwone. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę czerwoną, jest równe
A)  B)
B) 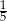 C)
C) 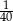 D)
D) 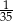
W pudełku jest 60 kul. Wśród nich jest 27 kul białych, 18 kul niebieskich, a pozostałe to kule żółte. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę, która nie jest niebieska, jest równe
A) 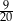 B)
B) 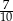 C)
C) 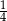 D)
D) 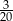
W równoległoboku 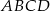 dłuższa podstawa ma długość
dłuższa podstawa ma długość 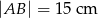 . Wysokości tego równoległoboku mają długości:
. Wysokości tego równoległoboku mają długości: 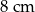 i
i 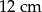 . Zatem krótsza podstawa równoległoboku ma długość
. Zatem krótsza podstawa równoległoboku ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
Poniżej zamieszczono fragment etykiety z sałatki z kurczakiem o masie 250 g.
| Wartość odżywcza | w 100 g |
| energia | 570 kJ/137 kcal |
| tłuszcz w tym kwasy nasycone | 9,5 g 1,6 g |
| węglowodany w tym cukry | 4,6 g 3,3 g |
| błonnik | 2,6 g |
| białko | 7,0 g |
| sól | 0,102 g |
| wapń | 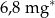 |
| potas | 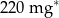 |
 1 mg=0,001 g
1 mg=0,001 g
Zjedzenie całej sałatki dostarcza organizmowi około A/B potasu.
A) 440 mg B) 550 mg
Zjedzenie całej sałatki dostarcza organizmowi C/D razy więcej soli niż wapnia.
C) 15 D) 150
Poniżej zamieszczono fragment etykiety z jogurtu o masie 150 g.
| Wartość odżywcza | w 100 g |
| energia | 290 kJ/69 kcal |
| tłuszcz w tym kwasy nasycone | 3,0 g 1,9 g |
| węglowodany w tym cukry | 5,9 g 5,9 g |
| błonnik | 0 g |
| białko | 4,6 g |
| sól | 0,15 g |
| wapń | 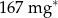 |
| witamina B2 | 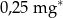 |
 1 mg=0,001 g
1 mg=0,001 g
Zjedzenie całego jogurtu dostarcza organizmowi około A/B wapnia.
A) 167 mg B) 250 mg
Zjedzenie całego jogurtu dostarcza organizmowi C/D razy więcej białka niż witaminy B2.
C) 18,4 D) 18 400
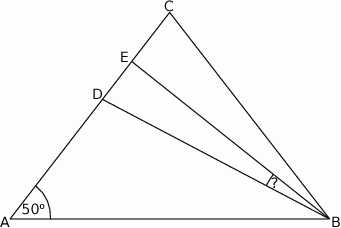
W trójkącie równoramiennym 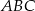 spełnione są warunki:
spełnione są warunki: 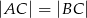 ,
, 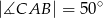 . Odcinek
. Odcinek 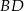 jest dwusieczną kąta
jest dwusieczną kąta 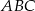 , a odcinek
, a odcinek 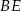 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 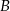 na bok
na bok 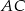 . Miara kąta
. Miara kąta 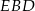 jest równa
jest równa
A) 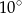 B)
B) 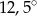 C)
C) 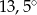 D)
D) 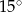
Z 24 kwadratów o boku długości 1 zbudowano prostokąt.
Która z podanych liczb nie może być obwodem otrzymanego prostokąta?
A) 20 B) 24 C) 28 D) 50
Końce odcinka 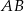 mają współrzędne
mają współrzędne 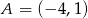 i
i 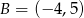 . Na symetralnej odcinka
. Na symetralnej odcinka 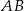 leży punkt o współrzędnych
leży punkt o współrzędnych
A) 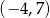 B)
B) 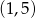 C)
C) 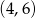 D)
D) 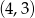
Dany jest zbiór 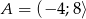 . Do zbioru
. Do zbioru 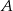 należy
należy
A) 12 liczb całkowitych i 5 liczb pierwszych
B) 13 liczb całkowitych i 9 liczb naturalnych
C) 6 liczb naturalnych i 4 liczby pierwsze
D) 12 liczb całkowitych i 4 liczby pierwsze
Rozwinięcie dziesiętne ułamka 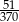 jest równe 0,1(378). Na pięćdziesiątym miejscu po przecinku tego rozwinięcia znajduje się cyfra
jest równe 0,1(378). Na pięćdziesiątym miejscu po przecinku tego rozwinięcia znajduje się cyfra
A) 1 B) 3 C) 7 D) 8
Rozwinięcie dziesiętne ułamka 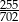 jest równe 0,3(632478). Na czterdziestym miejscu po przecinku tego rozwinięcia znajduje się cyfra
jest równe 0,3(632478). Na czterdziestym miejscu po przecinku tego rozwinięcia znajduje się cyfra
A) 2 B) 4 C) 7 D) 3
W jakim stosunku można podzielić odcinek o długości 36 cm, aby z otrzymanych czterech odcinków móc zbudować czworokąt?
A) 1 : 1 : 2 : 4 B) 1 : 2 : 2 : 6 C) 2 : 3 : 4 : 8 D) 2 : 3 : 3 : 8
Sześcian o objętości 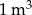 rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jedna z krawędzi powstałego prostopadłościanu miałaby długość 10 km. | P | F |
| Objętość prostopadłościanu byłaby 100 razy większa od objętości początkowego sześcianu. | P | F |
Z 1 000 000 sześcianów o objętości 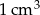 zbudowano prostopadłościan o polu podstawy równym
zbudowano prostopadłościan o polu podstawy równym 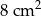 .
.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość prostopadłościanu jest równa 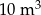 . . | P | F |
| Wysokość prostopadłościanu jest równa 1,25 km. | P | F |
Dane są trzy wyrażenia:
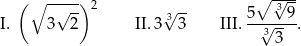
Wartości których wyrażeń są mniejsze od 5?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Dane są trzy wyrażenia:
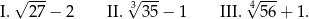
Wartości których wyrażeń są mniejsze od 4?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
W trójkącie równobocznym długość każdego boku zmniejszono o 20%. Wtedy pole tego trójkąta
A) zmniejszy się o 20% B) zmniejszy się o 40%
C) zmniejszy się o mniej niż 20% D) zmniejszy się o 36%
Wartość wyrażenia 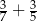 jest liczbą A/B.
jest liczbą A/B.
A) mniejszą od 1 B) większą od 1
Wartość wyrażenia 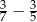 jest liczbą C/D.
jest liczbą C/D.
C) ujemną D) dodatnią
Wartość wyrażenia 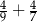 jest liczbą A/B.
jest liczbą A/B.
A) mniejszą od 1 B) większą od 1
Wartość wyrażenia 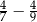 jest liczbą C/D.
jest liczbą C/D.
C) ujemną D) dodatnią
Poniżej zapisano trzy liczby:
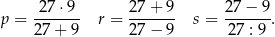
Który zapis przedstawia poprawnie uporządkowane liczby 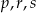 od najmniejszej do największej?
od najmniejszej do największej?
A) 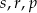 B)
B) 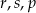 C)
C) 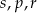 D)
D) 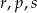
Poniżej zapisano trzy liczby:
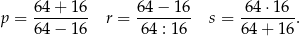
Który zapis przedstawia poprawnie uporządkowane liczby 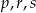 od największej do najmniejszej?
od największej do najmniejszej?
A) 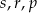 B)
B) 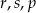 C)
C) 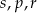 D)
D) 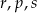
Dwie spośród liczb 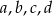 są dodatnie, a dwie ujemne.
są dodatnie, a dwie ujemne.
Ile najwięcej liczb ujemnych może być pośród liczb 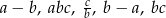 ?
?
A) Dwie. B) Trzy. C) Cztery. D) Pięć.
Prostopadłościenne paczki wysyłane za pośrednictwem firmy kurierskiej dzielone są na 5 kategorii w zależności od rozmiarów paczki.

| Kategoria | najdłuższy bok + najkrótszy bok |
| XS | 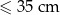 |
| S | 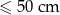 |
| M | 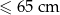 |
| L | 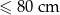 |
| XL | 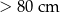 |
Do podanych wymiarów paczek dopisz odpowiadającą im kategorię.
| Wymiary | Kategoria |
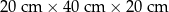 | |
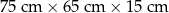 |

