Pola dwóch trójkątów równobocznych są równe odpowiednio 7 i 63.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód drugiego trójkąta jest 9 razy większy od obwodu pierwszego trójkąta. | P | F |
Pierwszy trójkąt jest podobny do drugiego w skali 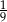 | P | F |

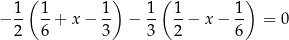
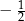
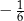
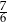
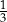
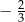
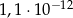 ma objętość równą
ma objętość równą 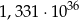
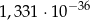
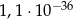
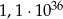
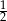 i
i 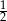
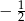 i 1.
i 1. 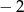 i
i 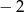
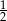 i
i 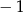

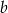
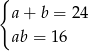
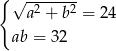
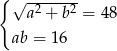
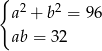
 , drugi ma miarę o
, drugi ma miarę o 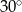 większą niż kąt
większą niż kąt  , a trzeci ma miarę trzy razy większą niż kąt
, a trzeci ma miarę trzy razy większą niż kąt  . Trójkąt ten jest
. Trójkąt ten jest  , drugi ma miarę o
, drugi ma miarę o 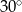 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  . Trójkąt ten jest
. Trójkąt ten jest  , drugi ma miarę o
, drugi ma miarę o 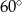 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  .
. 
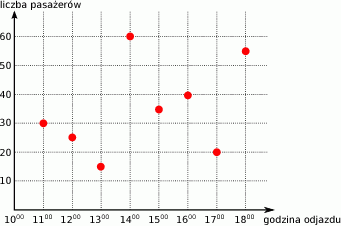
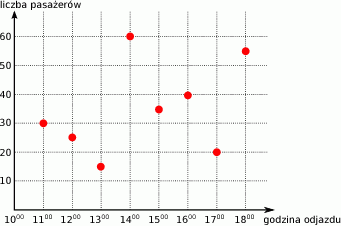
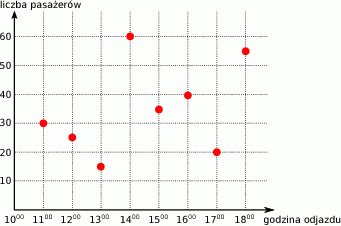
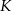 ,
, 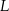 i
i 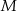 są środkami boków
są środkami boków 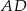 ,
, 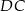 i
i 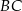 kwadratu
kwadratu 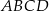 (rysunek).
(rysunek). 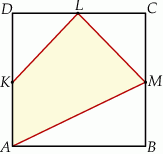
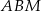 stanowi
stanowi 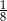 pola kwadratu
pola kwadratu 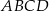 .
. 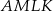 stanowi połowę pola kwadratu
stanowi połowę pola kwadratu 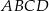 .
.
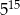 .
. 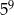 .
.
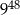 .
. 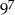 .
.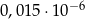 jest równa
jest równa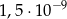
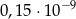
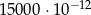
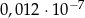 jest równa
jest równa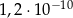
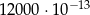
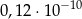
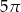 ma miarę
ma miarę 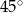 . Pole koła ograniczonego tym okręgiem jest równe
. Pole koła ograniczonego tym okręgiem jest równe 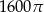
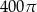
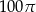
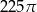
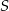 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 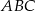 , a punkty
, a punkty 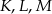 są punktami styczności tego okręgu z bokami trójkąta. Odcinek
są punktami styczności tego okręgu z bokami trójkąta. Odcinek 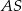 ma długość 26 cm, a odcinek
ma długość 26 cm, a odcinek 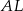 ma długość 24 cm.
ma długość 24 cm. 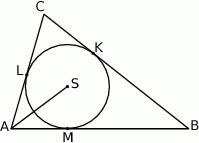
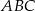 jest równy 9 cm.
jest równy 9 cm.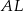 i
i 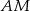 mają tę samą długość.
mają tę samą długość. 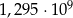
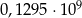
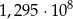
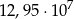
 złożonym z dwóch liczb dwucyfrowych oddzielonych literą
złożonym z dwóch liczb dwucyfrowych oddzielonych literą 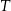 . Pierwsza liczba hasła to sześcian liczby 4, a druga to najmniejszy wspólny mianownik ułamków
. Pierwsza liczba hasła to sześcian liczby 4, a druga to najmniejszy wspólny mianownik ułamków 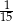 i
i 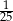 . Jakie jest hasło do pliku?
. Jakie jest hasło do pliku?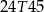
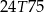
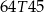
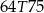
 złożonym z dwóch liczb dwucyfrowych oddzielonych literą
złożonym z dwóch liczb dwucyfrowych oddzielonych literą 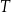 . Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków
. Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków 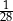 i
i 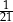 , a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?
, a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?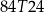
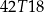
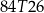
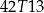
 ma długość 2, a obwód kwadratu
ma długość 2, a obwód kwadratu 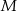 ma długość 16. Skala podobieństwa kwadratu
ma długość 16. Skala podobieństwa kwadratu 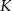 do kwadratu
do kwadratu 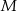 jest równa:
jest równa: 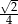
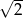
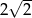
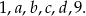
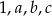 jest dwa razy mniejsza od mediany liczb
jest dwa razy mniejsza od mediany liczb 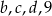 , a średnia arytmetyczna liczb
, a średnia arytmetyczna liczb 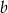 i
i  jest liczbą naturalną. Mediana liczb
jest liczbą naturalną. Mediana liczb 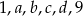 jest równa
jest równa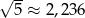 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 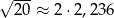
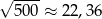
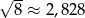 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 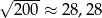
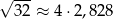
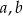 i
i  , które spełniają warunek
, które spełniają warunek 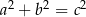 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów: 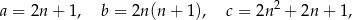
 oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (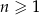 ).
). zawsze będzie A/B.
zawsze będzie A/B.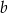 i
i  różnią się o C/D.
różnią się o C/D.
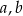 i
i  , które spełniają warunek
, które spełniają warunek 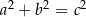 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów: 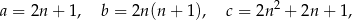
 oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (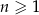 ).
).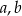 i
i  jest równa 11, to największa z tych liczb jest równa
jest równa 11, to największa z tych liczb jest równa 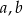 i
i  , które spełniają warunek
, które spełniają warunek 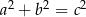 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów: 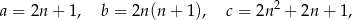
 oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (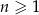 ).
).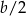 zawsze będzie A/B.
zawsze będzie A/B.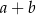 i
i  różnią się o C/D.
różnią się o C/D.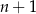
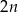
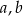 i
i  , które spełniają warunek
, które spełniają warunek 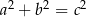 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów: 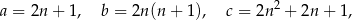
 oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (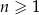 ).
).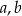 i
i  jest równa 9, to największa z tych liczb jest równa
jest równa 9, to największa z tych liczb jest równa 