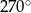Na siatce kwadratowej narysowano trójkąt. Bok kwadratu siatki jest równy 1.
Obwód narysowanego trójkąta jest równy
A) 76 B) 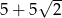 C)
C) 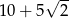 D) 75
D) 75
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
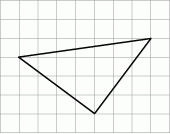
Na siatce kwadratowej narysowano trójkąt. Bok kwadratu siatki jest równy 1.

Obwód narysowanego trójkąta jest równy
A) 76 B) 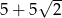 C)
C) 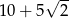 D) 75
D) 75
W sadzie rosną drzewa owocowe: grusze i jabłonie. Liczba grusz jest o 40% większa od liczby jabłoni. Jabłoni jest o 50 mniej niż grusz. Ile jabłoni rośnie w tym sadzie?
A) 20 B) 30 C) 70 D) 125
W sadzie rosną drzewa owocowe: grusze i jabłonie. Liczba jabłoni jest o 40% większa od liczby grusz. Grusz jest o 30 mniej niż jabłoni. Ile jabłoni rośnie w tym sadzie?
A) 90 B) 105 C) 75 D) 125
Cena brutto = cena netto + podatek VAT
Jeżeli stawka podatku VAT jest równa 22% i cenna brutto towaru jest równa 4392 zł to cena netto tego towaru jest równa
A) 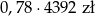 B)
B) 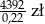 C)
C) 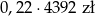 D)
D) 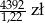
Liczby naturalne od 1 do 8 umieszczono w wierzchołkach sześcianu w ten sposób, że w żadnych dwóch wierzchołkach nie umieszczono tej samej liczby. Następnie na każdej krawędzi sześcianu umieszczono sumę liczb, które znajdują się na końcach tej krawędzi, a na środku każdej ściany umieszczono sumę liczb, które znajdują w wierzchołkach tej ściany. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Suma wszystkich liczb umieszczonych na krawędziach sześcianu jest równa 72. | P | F |
| Suma wszystkich liczb umieszczonych w środkach ścian sześcianu jest równa 144. | P | F |
W pewnej firmie zatrudnionych jest więcej niż 10 pracowników. Połowa z nich zarabia po 3000 zł, a druga połowa – po 4000 zł. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia arytmetyczna zarobków w tej firmie jest równa 3500 zł. | P | F |
| Gdy z pracy w tej firmie zrezygnują dwie osoby, z których jedna zarabia 3000 zł, a druga 4000 zł, to średnia arytmetyczna zarobków się nie zmieni. | P | F |
Pewnym samolotem podróżowało więcej niż 100 pasażerów. Dwie trzecie z nich zapłaciło za przewóz bagażu po 400 zł, a pozostali – po 100 zł. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia arytmetyczna opłat za przewóz bagażu w tym samolocie jest równa 200 zł. | P | F |
| Gdyby z podróży zrezygnowały trzy osoby, z których jedna zapłaciła za bagaż 100 zł, a dwie zapłaciły za bagaż po 400 zł, to średnia arytmetyczna opłat za przewóz bagażu w tym samolocie się nie zmieni. | P | F |
Cztery kartoniki z cyframi 0, 0, 1, 4 układamy tak, aby otrzymać liczbę czterocyfrową.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jest 12 liczb czterocyfrowych, które możemy utworzyć w ten sposób. | P | F |
Prawdopodobieństwo, że utworzona w ten sposób liczba czterocyfrowa dzieli się przez 4 jest równe 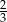 . . | P | F |
Ewa, Maciek i Julian mają razem 47 lat. Za ile lat będą mieli razem 59 lat?
A) 6 B) 4 C) 3 D) 12
Oskar jest o 6 lat starszy od swoich braci bliźniaków. Obecnie Oskar i jego dwaj bracia mają razem 42 lata. Ile lat ma obecnie każdy z bliźniaków?
A) 18 B) 16 C) 14 D) 12
W dwóch zbiornikach znajduje się 420 litrów mleka. Jeśli z pierwszego zbiornika przelejemy do drugiego  jego zawartości, to w obu zbiornikach będzie taka sama ilość mleka.
jego zawartości, to w obu zbiornikach będzie taka sama ilość mleka.
Ile litrów mleka jest w pierwszym zbiorniku?
A) 175 B) 229 C) 245 D) 252
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
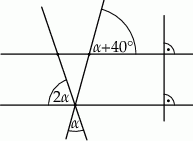
A) 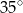 B)
B) 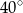 C)
C) 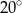 D)
D) 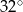
Wśród pewnej grupy osób przeprowadzono ankietę. Jedno z pytań brzmiało: Jaka jest twoja ulubiona pora roku?. Każdy ankietowany wskazał tylko jedną porę roku. Rozkład udzielonych odpowiedzi na to pytanie przedstawiono na diagramie.
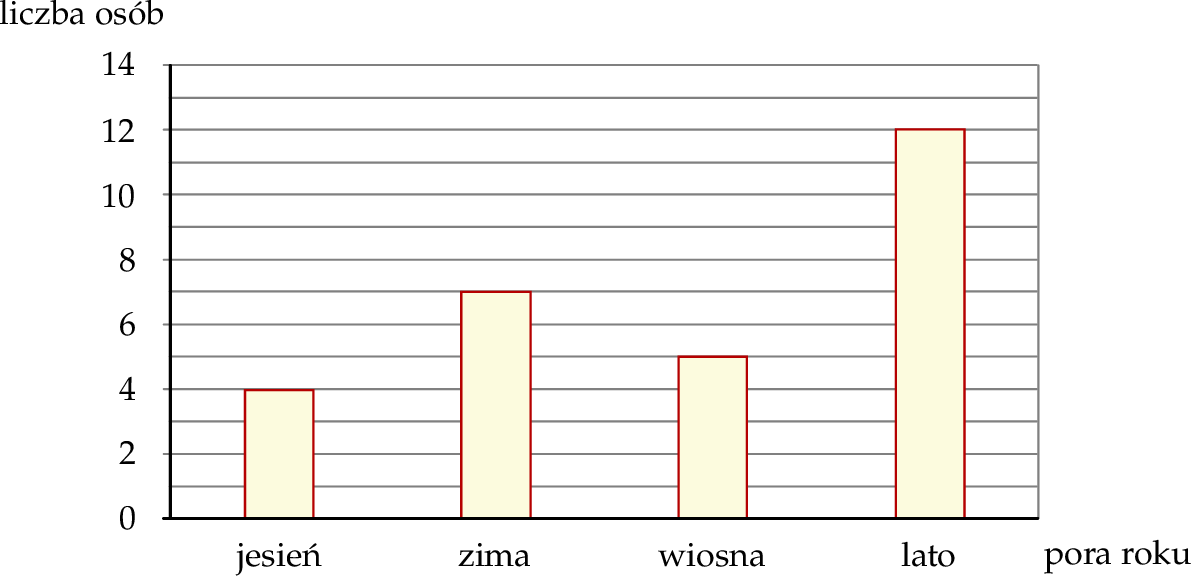
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Zima jest ulubioną porą roku dla mniej niż 24% liczby osób ankietowanych. | P | F |
Lato jest ulubioną porą roku dla  liczby osób ankietowanych. liczby osób ankietowanych. | P | F |
Wśród pewnej grupy osób przeprowadzono ankietę. Jedno z pytań brzmiało: Jaka jest twoja ulubiona pora roku?. Każdy ankietowany wskazał tylko jedną porę roku. Rozkład udzielonych odpowiedzi na to pytanie przedstawiono na diagramie.
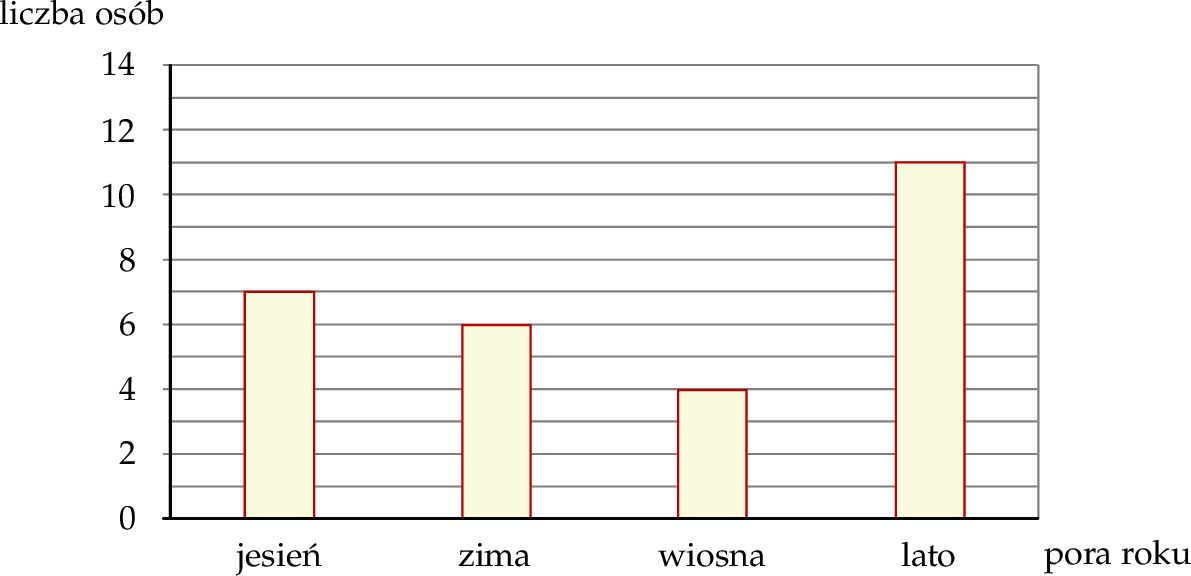
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Zima jest ulubioną porą roku dla więcej niż 20% liczby osób ankietowanych. | P | F |
Wiosna jest ulubioną porą roku dla  liczby osób ankietowanych. liczby osób ankietowanych. | P | F |
Dane są dwie liczby
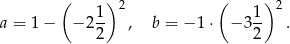
Wartość wyrażenia 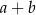 jest równa A/B.
jest równa A/B.
A) 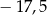 B) 18,5
B) 18,5
Wartość wyrażenia 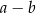 jest równa C/D.
jest równa C/D.
C) 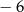 D) 7
D) 7
Mateusz mieszka w odległości 4 km od szkoły. Część drogi do szkoły pokonuje pieszo, idąc do przystanku autobusowego. Tam czeka na autobus, a następnie wsiada do niego i jedzie do szkoły. Pewnego dnia, gdy był już na przystanku, stwierdził, że zapomniał zabrać zeszyt, więc wrócił po niego do domu. Wykres przedstawia, jak tego dnia zmieniała się odległość Mateusza od domu w zależności od czasu.
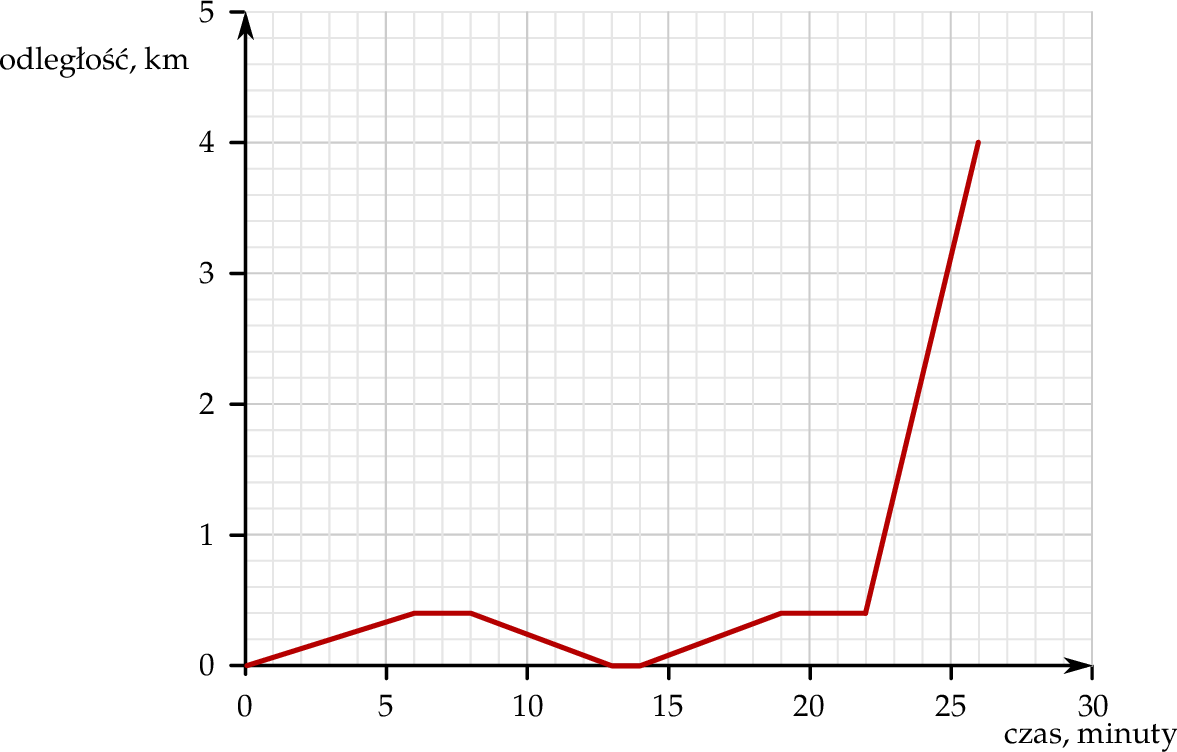
Od momentu, gdy Mateusz zawrócił z przystanku do domu, do momentu, gdy dotarł ponownie na przystanek, upłynęło
A) 11 minut. B) 13 minut. C) 14 minut. D) 16 minut.
Mateusz mieszka w odległości 4 km od szkoły. Część drogi do szkoły pokonuje pieszo, idąc do przystanku autobusowego. Tam czeka na autobus, a następnie wsiada do niego i jedzie do szkoły. Pewnego dnia, gdy był już na przystanku, stwierdził, że zapomniał zabrać zeszyt, więc wrócił po niego do domu. Wykres przedstawia, jak tego dnia zmieniała się odległość Mateusza od domu w zależności od czasu.
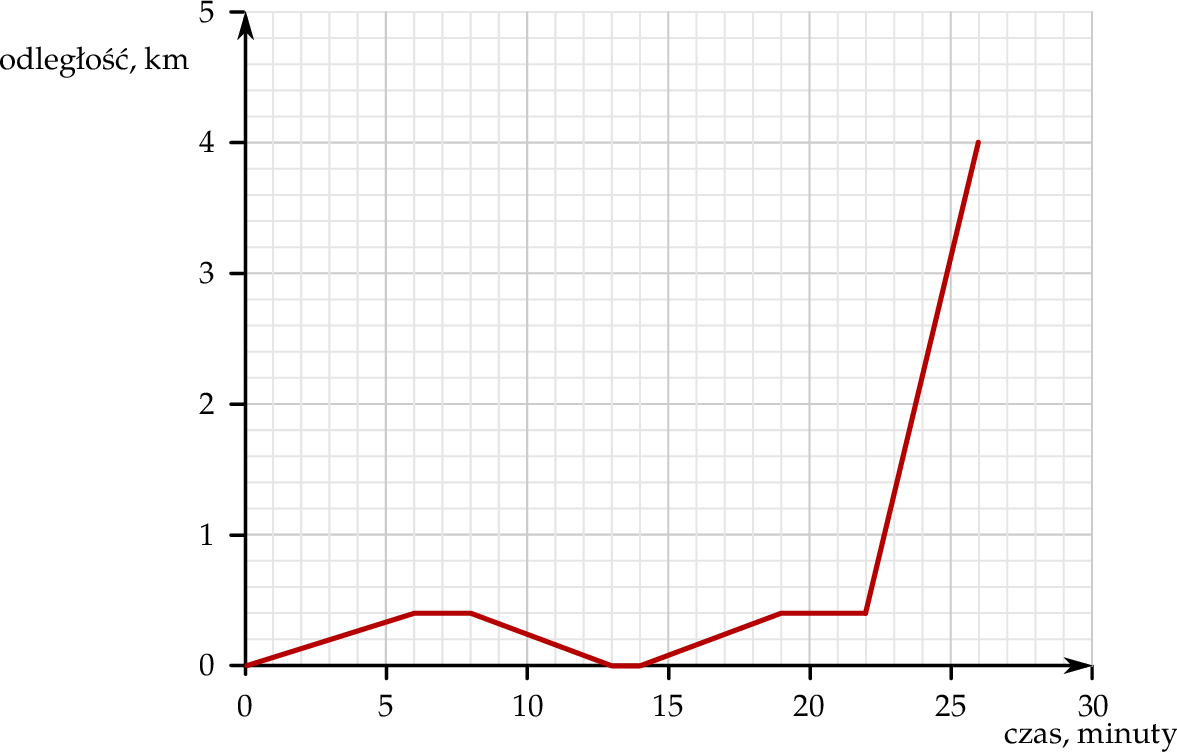
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dom Mateusza znajduje się w odległości 400 m od przystanku autobusowego. | P | F |
Autobus drogę między przystankami pokonał z prędkością 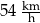 . . | P | F |
Rozwiązaniem równania 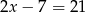 jest liczba
jest liczba
A) 7 B) 14 C) 26 D) 28
Miejscowości  i
i 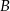 położone na przeciwległych brzegach jeziora są połączone dwiema drogami – drogą polną prowadzącą przez punkt
położone na przeciwległych brzegach jeziora są połączone dwiema drogami – drogą polną prowadzącą przez punkt 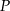 i drogą leśną prowadzącą przez punkt
i drogą leśną prowadzącą przez punkt 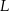 . Długość drogi polnej
. Długość drogi polnej 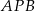 wynosi 10 km, a długość drogi leśnej
wynosi 10 km, a długość drogi leśnej 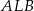 jest równa 6 km.
jest równa 6 km.
Matylda i Karol wyruszyli na rowerach z miejscowości  do miejscowości
do miejscowości  o godzinie 10:00. Matylda jechała drogą leśną, a Karol – drogą polną. Średnia prędkość jazdy Matyldy wynosiła
o godzinie 10:00. Matylda jechała drogą leśną, a Karol – drogą polną. Średnia prędkość jazdy Matyldy wynosiła 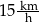 , a średnia prędkość Karola była równa
, a średnia prędkość Karola była równa 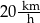 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Do miejscowości  Karol przyjechał wcześniej niż Matylda. Karol przyjechał wcześniej niż Matylda. | P | F |
Matylda przyjechała do miejscowości  o godzinie 10:24. o godzinie 10:24. | P | F |
Marta zapisała w systemie rzymskim cztery liczby: CLXX, CXC, CCLXX oraz CCL. Która z nich znajduje się na osi liczbowej najbliżej liczby 200?
A) CLXX B) CXC C) CCLXX D) CCL
Zmieszano 100 litrów mleka 2% i 25 litrów mleka 4%. Otrzymano mleko, które ma w sobie 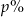 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 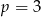 B)
B) 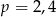 C)
C) 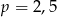 D)
D) 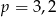
Zmieszano 25 litrów mleka 2% i 100 litrów mleka 4%. Otrzymano mleko, które ma w sobie 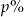 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 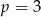 B)
B) 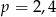 C)
C) 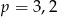 D)
D) 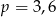
Zmieszano 2,5 szklanki octu 6% z 1,5 szklanki octu 10%. Jakie jest stężenie otrzymanej mieszanki?
A) 9% B) 8% C) 7% D) 7,5%
Zmieszano 15 g 20% roztworu z 25 g 12% roztworu. Stężenie procentowe otrzymanego roztworu jest równe
A) 15% B) 14% C) 16% D) 18%
Zmieszano 60 litrów mleka 2,5% i 40 litrów mleka 3%. Otrzymano mleko, które ma w sobie 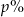 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 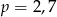 B)
B) 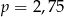 C)
C) 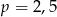 D)
D) 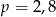
O liczbach 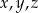 wiemy, że kwadrat ich iloczynu jest o 20% większy od odwrotności ich sumy. Która równość poprawnie opisuje zależność wiążącą liczby
wiemy, że kwadrat ich iloczynu jest o 20% większy od odwrotności ich sumy. Która równość poprawnie opisuje zależność wiążącą liczby 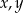 i
i  ?
?
A) 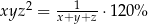 B)
B) 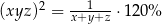
C) 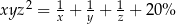 D)
D) 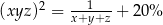
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
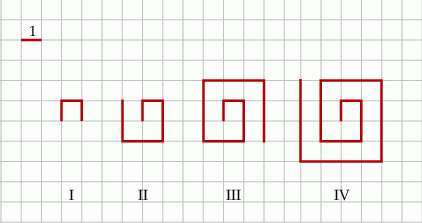
Długości tych łamanych zapisał w tabeli.
| Numer łamanej | I | II | III | IV |
| Długość łamanej | 3 | 8 | 15 | 24 |
Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Łamana o długości 48 ma numer A/B.
A) VI B) VII
Łamana o numerze VIII ma długość C/D.
C) 63 D) 80
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
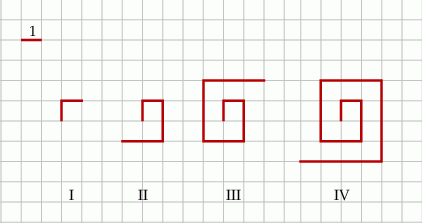
Długości tych łamanych zapisał w tabeli.
| Numer łamanej | I | II | III | IV |
| Długość łamanej | 2 | 6 | 12 | 20 |
Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Łamana o długości 56 ma numer A/B.
A) VI B) VII
Łamana o numerze VIII ma długość C/D.
C) 72 D) 80
Proste  i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 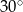 .
.
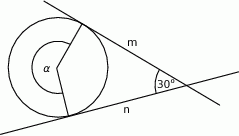
Miara kąta  jest równa
jest równa
A) 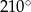 B)
B) 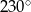 C)
C) 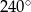 D)
D) 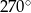
Proste 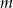 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 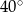 .
.
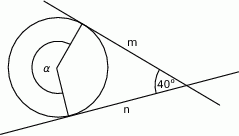
Miara kąta  jest równa
jest równa
A) 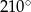 B)
B) 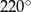 C)
C) 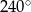 D)
D)