Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pięciu rzutach standardową sześcienną kostką do gry, jeżeli wynik każdego rzutu będzie inny, można otrzymać łącznie dokładnie 20 oczek. | P | F |
| W 16 rzutach standardową sześcienną kostką do gry można otrzymać łącznie ponad 100 oczek. | P | F |

 jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.  może być równa 35.
może być równa 35.  może być równa 1024.
może być równa 1024. jego wysokości.
jego wysokości. 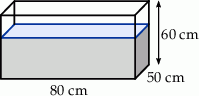
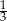 jego wysokości.
jego wysokości. 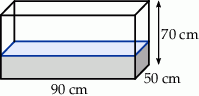
 tego zakładu można obliczyć, rozwiązując równanie
tego zakładu można obliczyć, rozwiązując równanie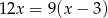
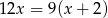
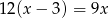
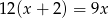
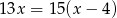
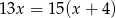
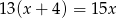
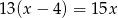
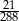 stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe 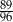
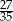
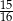
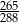
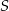 i kąt wpisany o mierze
i kąt wpisany o mierze 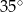 .
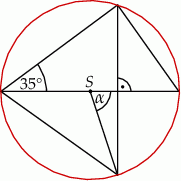
. 
 ma miarę
ma miarę 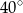
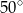
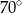
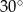
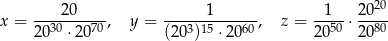
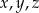 są większe od liczby
są większe od liczby 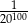 .
.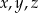 jest równa 0.
jest równa 0. 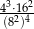 ma wartość
ma wartość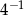
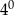
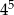
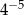
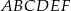 poprowadzono trzy przekątne wychodzące z wierzchołka
poprowadzono trzy przekątne wychodzące z wierzchołka 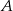 i utworzone przez nie kąty spełniają warunki:
i utworzone przez nie kąty spełniają warunki: 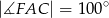 ,
, 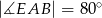 ,
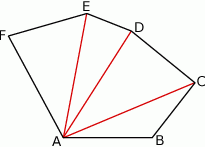
, 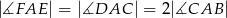 .
. 
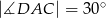
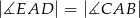
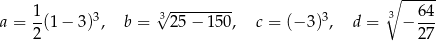
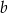 jest większa niż liczba
jest większa niż liczba  .
.  jest o 23 mniejsza niż liczba
jest o 23 mniejsza niż liczba  .
. 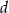 jest 3 razy mniejsza niż liczba
jest 3 razy mniejsza niż liczba  .
. 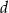 jest większa niż liczba
jest większa niż liczba 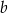 .
. 
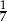 chodnika, drugiego dnia ułożyli
chodnika, drugiego dnia ułożyli 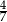 chodnika, a trzeciego resztę. Jaką część chodnika robotnicy ułożyli trzeciego dnia?
chodnika, a trzeciego resztę. Jaką część chodnika robotnicy ułożyli trzeciego dnia?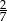
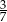
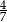
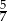
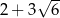 .
. 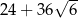
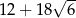
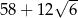
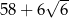
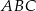 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy 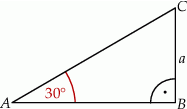
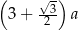
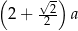
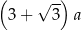
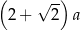
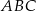 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy 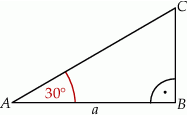
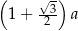
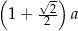
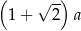
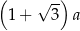
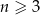 , to liczbę przekątnych wielokąta wypukłego o
, to liczbę przekątnych wielokąta wypukłego o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru 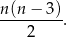
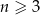 , to liczbę przekątnych wielokąta wypukłego o
, to liczbę przekątnych wielokąta wypukłego o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru 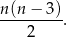
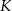 ,
, 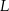 i środku w punkcie
i środku w punkcie 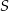 . Punkt
. Punkt 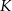 ma współrzędne
ma współrzędne 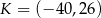 , a punkt
, a punkt 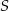 współrzędne
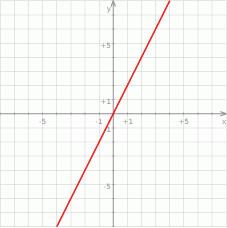
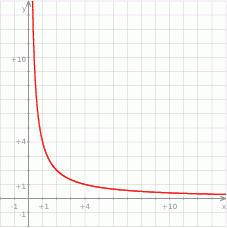
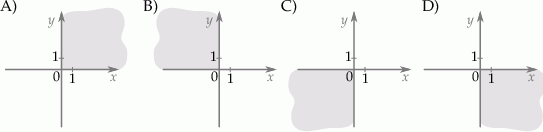
współrzędne 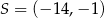 . Na którym rysunku zacieniowana część płaszczyzny zawiera punkt
. Na którym rysunku zacieniowana część płaszczyzny zawiera punkt 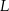 ?
? 
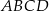 boki
boki 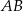 ,
, 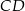 i
i 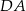 mają równe długości, a kąt
mają równe długości, a kąt 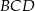 ma miarę
ma miarę 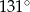 . Przekątna
. Przekątna 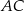 dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek). 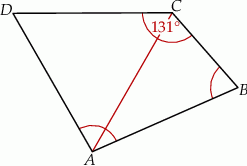
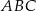 ma miarę
ma miarę 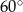 .
.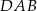 ma miarę
ma miarę 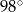 .
.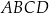 boki
boki 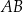 ,
, 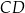 i
i 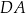 mają równe długości, a kąt
mają równe długości, a kąt 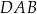 ma miarę
ma miarę 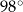 . Przekątna
. Przekątna 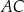 dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek). 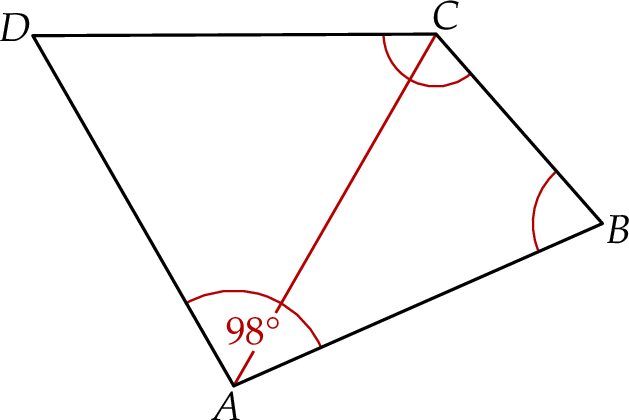
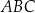 ma miarę
ma miarę 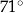 .
. 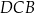 ma miarę
ma miarę 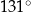 .
.