Cena płyty kompaktowej po 30% obniżce wynosi 49 zł. Cena tej płyty przed obniżką była równa
A) 14,70 zł. B) 34,30 zł. C) 63,70 zł. D) 70,00 zł.
/Szkoła podstawowa/Zadania testowe
Biuro podróży w ramach oferty promocyjnej obniżyło cenę wycieczki o 20%. Pani Anna skorzystała z promocji i za wycieczkę zapłaciła 1500 zł. Jaka była cena wycieczki przed obniżką?
A) 1800 zł. B) 1875 zł. C) 2000 zł. D) 2175 zł.
Cena filmu na płycie DVD po 20% obniżce wynosi 52 zł. Cena tego filmu przed obniżką była równa
A) 65 zł. B) 64 zł. C) 62,4 zł. D) 60 zł.
Biuro podróży w ramach oferty promocyjnej obniżyło cenę wycieczki o 25%. Pani Anna skorzystała z promocji i za wycieczkę zapłaciła 1800 zł. Jaka była cena wycieczki przed obniżką?
A) 2250 zł. B) 1875 zł. C) 2400 zł. D) 2160 zł.
Cena książki po podwyżce o 20% wynosi 84 zł. Cena tej książki przed podwyżką była równa
A) 70 zł. B) 56 zł. C) 67,20 zł. D) 82,35 zł.
Na rysunku przedstawiono romb i jego przekątne. Długości odcinków na jakie dzielą się przekątne tego rombu są opisane za pomocą wyrażeń.
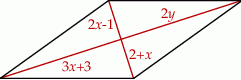
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód rombu jest równy 52. | P | F |
| Pole rombu jest równe 240. | P | F |
Na rysunku przedstawiono równoległobok 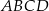 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek symetrii równoległoboku  ma współrzędne ma współrzędne 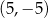 . . | P | F |
Wierzchołek 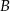 ma współrzędne ma współrzędne 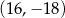 . . | P | F |
Na wykresie przedstawiono wysokość zarobków 6 pracowników pewnego przedsiębiorstwa.
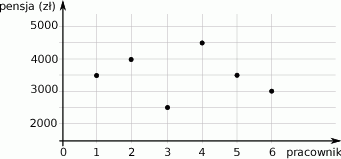
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli każdy z pierwszych 3 pracowników otrzyma 10% podwyżkę, to łącznie będą zarabiać więcej niż w sumie zarabiają pracownicy nr 4, 5 i 6. | P | F |
| Zarobki pracownika nr 5 są o 36% wyższe od zarobków pracownika nr 3. | P | F |
W dwóch wannach jest woda. W pierwszej wannie są 252 litry wody. Ile litrów wody jest w drugiej wannie, jeżeli wiadomo, że jest jej o  mniej niż w pierwszej wannie?
mniej niż w pierwszej wannie?
A) 42 B) 192 C) 246 D) 210
Ostrosłupy prawidłowe trójkątne 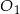 i
i 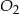 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 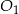 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 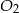 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 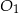 do objętości ostrosłupa
do objętości ostrosłupa 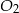 jest równy
jest równy
A) 3 : 1 B) 1 : 3 C) 9 : 1 D) 1 : 9
Jeżeli 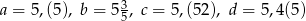 , to
, to
A) 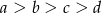 B)
B) 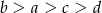 C)
C) 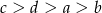 D)
D) 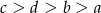
Jeżeli 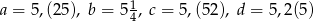 , to
, to
A) 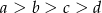 B)
B) 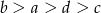 C)
C) 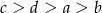 D)
D) 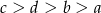
Jeżeli 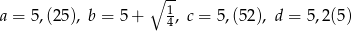 , to
, to
A) 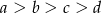 B)
B) 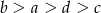 C)
C) 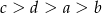 D)
D) 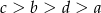
Pewnego dnia w klasie liczącej 11 dziewcząt i 15 chłopców nieobecny był jeden chłopiec i jedna dziewczynka. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 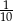 B)
B) 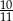 C)
C) 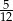 D)
D) 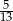
Pewnego dnia w klasie liczącej 16 dziewcząt i 12 chłopców nieobecnych było dwóch chłopców i trzy dziewczynki. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 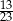 B)
B) 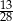 C)
C) 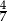 D)
D) 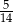
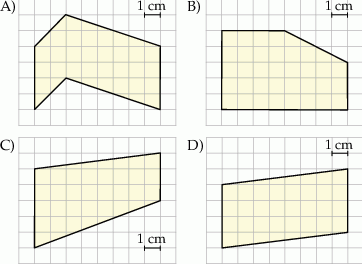
Na rysunkach zaznaczono cztery wielokąty o wierzchołkach w punktach przecięcia się linii siatki. Wskaż wielokąt, którego pole jest inne niż pola trzech pozostałych wielokątów.
Kąt ostry rombu ma miarę 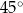 , a jego bok ma długość
, a jego bok ma długość  .
.
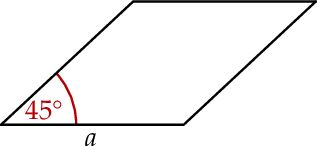
Pole tego rombu można wyrazić wzorem
A) 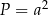 B)
B) 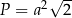 C)
C) 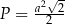 D)
D) 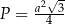
Wskaż liczbę, której 4% jest równe 8.
A) 3,2 B) 32 C) 100 D) 200
Jeżeli 8,5% liczby  jest równe 163,2, to liczba
jest równe 163,2, to liczba  jest równa
jest równa
A) 19200 B) 1920 C) 1387,2 D) 13872
4,5% liczby  jest równe 48,6. Liczba
jest równe 48,6. Liczba  jest równa
jest równa
A) 1080 B) 108 C) 48,6 D) 4,86
Wskaż liczbę, której 0,4% jest równe 12.
A) 0,048 B) 0,48 C) 30 D) 3000
Liczba 42 jest równa 0,6% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 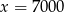 B)
B) 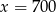 C)
C) 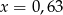 D)
D) 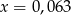
Jeżeli 35% pewnej liczby  jest równe 140 to
jest równe 140 to
A) 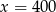 B)
B) 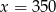 C)
C) 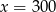 D)
D) 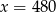
Liczba 78 stanowi 150% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 60 B) 52 C) 48 D) 39
Liczba 609 stanowi 140% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 420 B) 435 C) 468 D) 406
Wskaż liczbę, której 6% jest równe 6.
A) 0,36 B) 3,6 C) 10 D) 100
Kąty wewnętrzne przy wierzchołkach 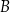 i
i 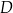 trapezu
trapezu 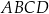 są równe odpowiednio
są równe odpowiednio 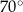 i
i 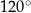 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 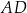 i
i 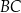 przecinają się pod kątem
przecinają się pod kątem
A) 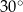 B)
B) 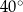 C)
C) 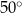 D)
D) 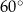
Kąty wewnętrzne przy wierzchołkach 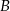 i
i 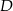 trapezu
trapezu 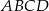 są równe odpowiednio
są równe odpowiednio 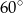 i
i 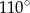 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 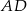 i
i 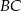 przecinają się pod kątem
przecinają się pod kątem
A) 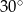 B)
B) 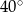 C)
C) 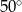 D)
D) 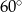
Długość przekątnej prostokąta przedstawionego na rysunku jest równa
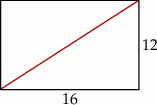
A) 12 B) 16 C) 18 D) 20
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15
Na rysunku przedstawiono liczbę i rodzaj kul umieszczonych w każdym z czterech pudełek. Z każdego pudełka losujemy jedną kulę.
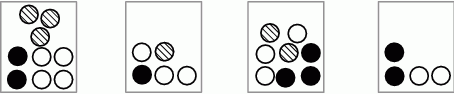
Prawdopodobieństwo wylosowania białej kuli jest największe, gdy kulę losujemy z pudełka
A) 1 B) 2 C) 3 D) 4
W tabeli przedstawiono liczbę i rodzaj kul umieszczonych w czterech pudełkach. Z każdego pudełka losujemy jedną kulę.
| Liczba kul zielonych | Liczba kul niebieskich | Liczba kul czerwonych | |
| Pudełko nr 1 | 4 | 8 | 5 |
| Pudełko nr 2 | 7 | 16 | 9 |
| Pudełko nr 3 | 2 | 7 | 3 |
| Pudełko nr 4 | 7 | 12 | 5 |
Prawdopodobieństwo wylosowania niebieskiej kuli jest największe, gdy kulę losujemy z pudełka nr
A) 1 B) 2 C) 3 D) 4
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 22% B) 33% C) 45% D) 63%
Na seans filmowy sprzedano 420 biletów, w tym 189 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 63% B) 45% C) 33% D) 22%
Na seans filmowy sprzedano 280 biletów, w tym 84 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 14% B) 22% C) 30% D) 42%
Na koncert sprzedano 680 biletów, w tym 306 na miejsca siedzące. Jaki procent sprzedanych biletów stanowiły bilety na miejsca siedzące?
A) 63% B) 45% C) 33% D) 22%
Ze zbiornika I, w którym znajdowało się 100 litrów wody, przelewano wodę do zbiornika II. Na wykresie przedstawiono, jak zmieniała się objętość wody w zbiorniku II od chwili, w której rozpoczęto przelewanie ze zbiornika I.
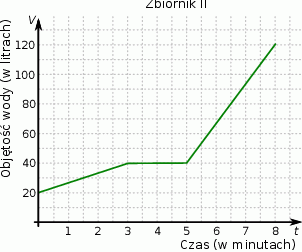
Uzupełnij zdania.
W chwili rozpoczęcia przelewania w zbiorniku II znajdowało się . . . . . . . . . litrów wody.
W ciągu pierwszych trzech minut ze zbiornika I do zbiornika II przelano . . . . . . . . litrów wody, a w ciągu pierwszych pięciu minut przelano . . . . . . . . . litrów.
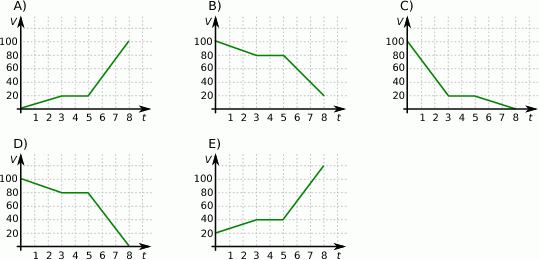
Ze zbiornika I, w którym znajdowało się 100 litrów wody, przelewano wodę do zbiornika II. Na wykresie przedstawiono, jak zmieniała się objętość wody w zbiorniku II od chwili, w której rozpoczęto przelewanie ze zbiornika I.
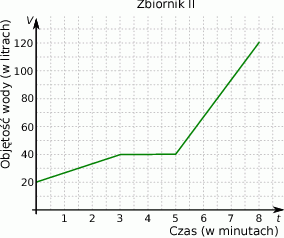
Na którym z poniższych wykresów przedstawiono, jak zmieniała się objętość wody w zbiorniku I w czasie przelewania?
Na rysunku przedstawiono dwie bryły. Bryła I jest sześcianem o boku 5, a bryła II powstała z sześcianu o boku 5 przez usunięcie 6 sześcianów jednostkowych.
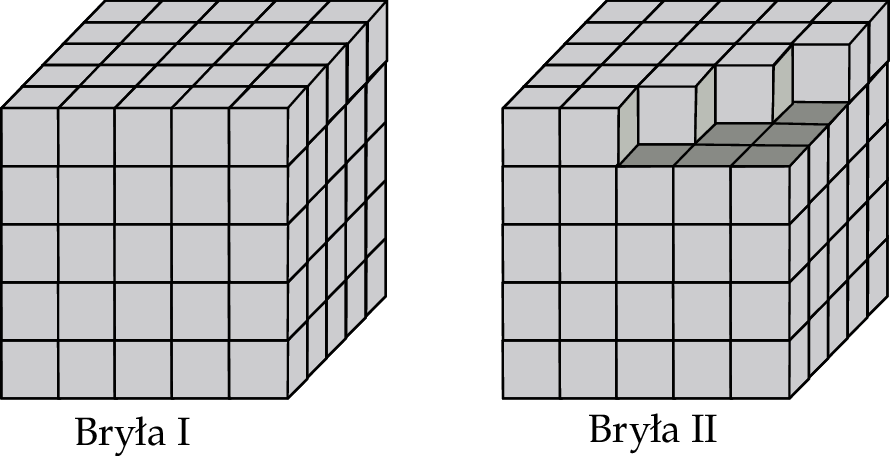
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bryła II ma większe pole powierzchni niż bryła I. | P | F |
| Objętość bryły II przekracza 90% objętości bryły I | P | F |
W tabeli zapisano cztery liczby.
| I | 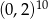 |
| II | 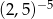 |
| III | 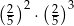 |
| IV | 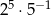 |
Liczba 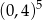 jest równa liczbom
jest równa liczbom
A) I i II B) I i III C) II i IV D) II i III E) III i IV
Dane są liczby  i
i 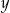 spełniające warunki:
spełniające warunki: 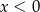 i
i 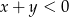 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 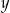 musi być ujemna. musi być ujemna. | P | F |
Liczby  i i 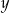 mogą być równe. mogą być równe. | P | F |
Suma liczb  i
i 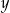 jest liczbą ujemną, a ich iloczyn jest liczbą dodatnią.
jest liczbą ujemną, a ich iloczyn jest liczbą dodatnią.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 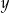 są różnych znaków. są różnych znaków. | P | F |
| Na osi liczbowej odległość każdej z tych liczb od 0 jest nie mniejsza od 1. | P | F |
Dane są liczby  i
i 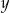 spełniające warunek:
spełniające warunek: 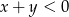 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 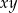 nie może być dodatnia. nie może być dodatnia. | P | F |
Liczba 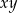 może być równa 0. może być równa 0. | P | F |
Suma liczb  i
i 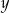 jest liczbą dodatnią, a ich iloczyn jest liczbą ujemną.
jest liczbą dodatnią, a ich iloczyn jest liczbą ujemną.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 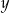 są różnych znaków. są różnych znaków. | P | F |
| Na osi liczbowej odległość każdej z tych liczb od zera jest taka sama. | P | F |
Dane są liczby  i
i 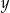 spełniające warunek:
spełniające warunek: 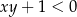 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 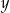 mają różne znaki. mają różne znaki. | P | F |
Suma liczb  i i 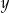 może być dodatnia. może być dodatnia. | P | F |

