Długość modelu samolotu Albatros D.V wykonanego w skali 1:48 wynosi 153 mm. Długość samolotu Albatros D.V wynosi około
A) 7,34 m B) 74 m C) 0,74 m D) 7,4 m
/Szkoła podstawowa/Zadania testowe
Na planie miasta wykonanym w skali 1:5000 odległość w linii prostej między punktem oznaczającym wejście do papugarni a punktem oznaczającym wejście do muzeum zabawek jest równa 8,4 cm. W terenie odległość między wejściami do tych obiektów jest w linii prostej równa
A) 4,2 m B) 42 m C) 420 m D) 4200 m
Na planie miasta odległość w linii prostej od punktu oznaczającego przystanek autobusowy Dworzec do punktu oznaczającego przystanek autobusowy Galeria jest równa 8 cm. Plan miasta został wykonany w skali 1 : 4 000.
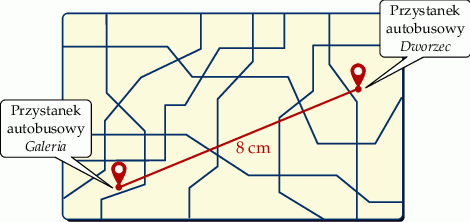
Odległość w linii prostej w terenie między tymi przystankami jest równa
A) 320 m B) 500 m C) 3 200 m D) 5 000m
Na planie miasta odległość w linii prostej od punktu oznaczającego przystanek autobusowy Uniwersytet do punktu oznaczającego przystanek autobusowy Muzeum jest równa 12 cm. Plan miasta został wykonany w skali 1 : 5 000.
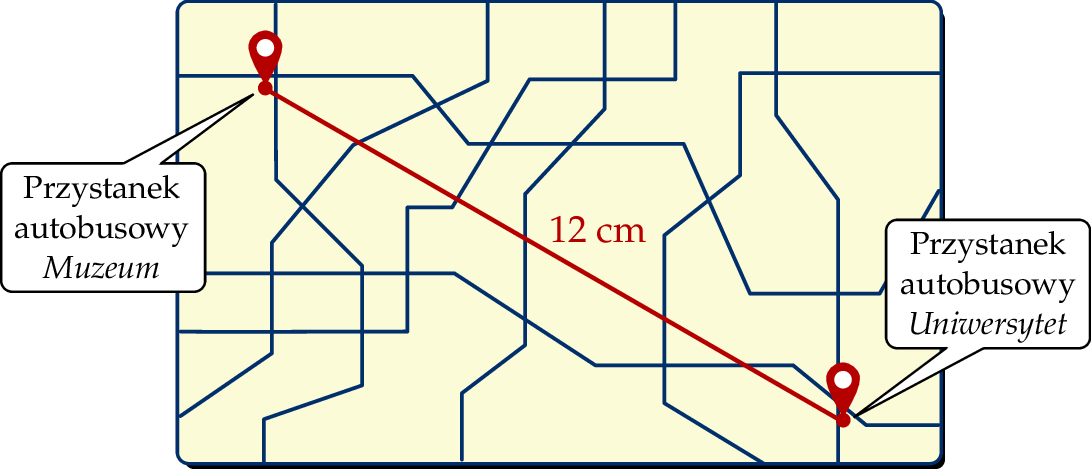
Odległość w linii prostej w terenie między tymi przystankami jest równa
A) 2 400 m B) 600 m C) 3 200 m D) 6 000m
Wykres przedstawia zależność drogi przebytej przez samochód jadący z miasta 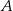 do miasta
do miasta 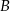 w zależności od czasu jazdy.
w zależności od czasu jazdy.
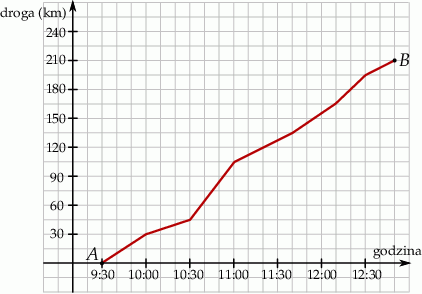
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Samochód przejechał drugą połowę trasy szybciej niż pierwszą połowę. | P | F |
| Pół godziny przez zakończeniem podróży samochód miał jeszcze do przejechania 30 km. | P | F |
Wykres przedstawia zależność drogi przebytej przez samochód jadący z miasta 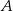 do miasta
do miasta 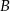 w zależności od czasu jazdy.
w zależności od czasu jazdy.
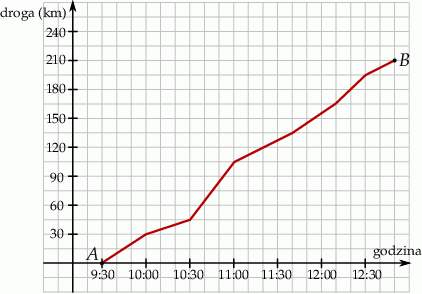
Z jaką największą prędkością poruszał się samochód?
A) 150 km/h B) 90 km/h C) 60 km/h D) 120 km/h
Małgosia narysowała równoległobok położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego równoległoboki rysowała w taki sposób, że dolny lewy wierzchołek rysowanego równoległoboku był środkiem górnego boku poprzedniego równoległoboku (rysunek 2.).
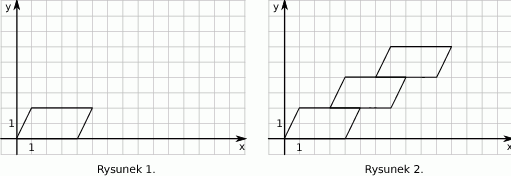
Małgosia narysowała w opisany sposób czwarty równoległobok. Współrzędna
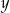 prawego górnego wierzchołka tego równoległoboku jest równa
prawego górnego wierzchołka tego równoległoboku jest równaA) 8 B) 9 C) 10 D) 11
Małgosia narysowała równoległobok położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego równoległoboki rysowała w taki sposób, że dolny lewy wierzchołek rysowanego równoległoboku był środkiem górnego boku poprzedniego równoległoboku (rysunek 2.).
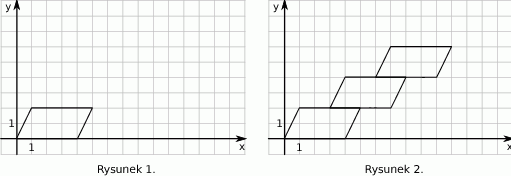
Agnieszka narysowała w taki sam sposób
 równoległoboków. Współrzędna y prawego górnego wierzchołka ostatniego równoległoboku jest równa
równoległoboków. Współrzędna y prawego górnego wierzchołka ostatniego równoległoboku jest równaA)
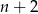 B)
B) 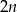 C)
C) 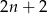 D)
D) 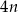
Małgosia narysowała równoległobok położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego równoległoboki rysowała w taki sposób, że dolny lewy wierzchołek rysowanego równoległoboku był środkiem górnego boku poprzedniego równoległoboku (rysunek 2.).
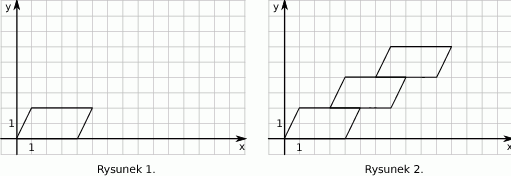
Współrzędne prawego górnego wierzchołka ostatniego narysowanego równoległoboku są równe
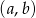 . Współrzędne takiego wierzchołka w następnym równoległoboku będą równe
. Współrzędne takiego wierzchołka w następnym równoległoboku będą równeA)
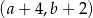 B)
B) 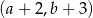 C)
C) 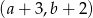 D)
D) 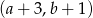
Cenę pewnego towaru obniżono o 25%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 20% B) o 33,(3)% C) o 15,(2)% D) o 22%
Cenę pewnego towaru obniżono o 20%. O ile procent należy podnieść obecną cenę tego towaru, aby otrzymać cenę początkową?
A) o 20% B) o 33,(3)% C) o 25% D) o 30%
Cenę  pewnego towaru obniżono o 36% i otrzymano cenę
pewnego towaru obniżono o 36% i otrzymano cenę 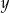 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 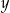 należy podnieść o
należy podnieść o
A) o 64% B) o 60% C) o 36% D) o 56,25%
Cenę  pewnego towaru obniżono o 20% i otrzymano cenę
pewnego towaru obniżono o 20% i otrzymano cenę 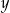 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 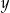 należy podnieść o
należy podnieść o
A) o 25% B) o 20% C) o 15% D) o 12%
Na rysunku przedstawiono trójkąt równoramienny 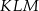 o ramionach
o ramionach 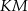 i
i 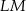 . Miara kąta
. Miara kąta 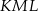 jest dwa razy większa niż miara kąta
jest dwa razy większa niż miara kąta 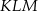 .
.
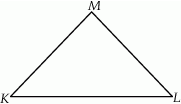
Miara kąta 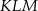 jest równa A/B.
jest równa A/B.
A) 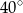 B)
B) 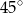
Trójkąt 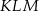 jest C/D.
jest C/D.
C) rozwartokątny D) prostokątny
Na wykresie przedstawiono zależność pola pomalowanej powierzchni od ilości zużytej farby. Pole pomalowanej powierzchni jest wprost proporcjonalne do ilości zużytej farby.
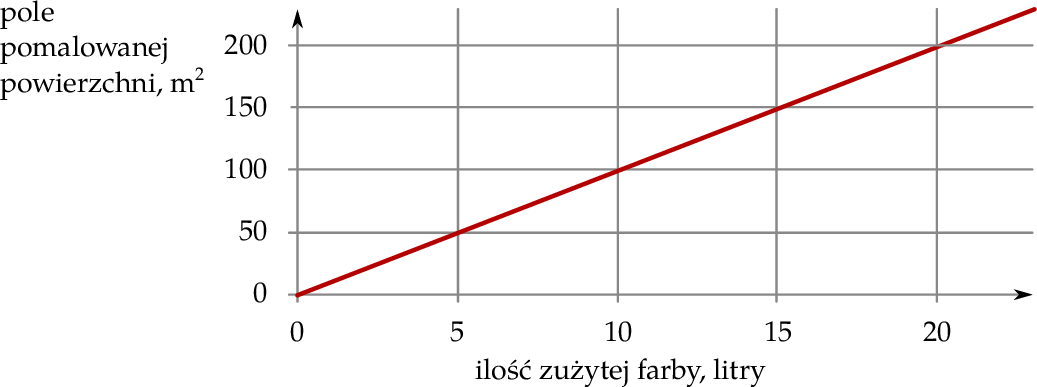
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
18 litrów tej farby wystarczy na pomalowanie 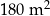 powierzchni. powierzchni. | P | F |
Na pomalowanie 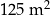 powierzchni wystarczy 12 litrów tej farby. powierzchni wystarczy 12 litrów tej farby. | P | F |
W prostokątnym układzie współrzędnych przedstawiono wykres funkcji, która jest określona dla liczb z przedziału 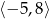 .
.
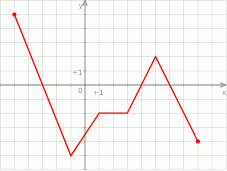
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość 1 dla argumentów 4 i 6. | P | F |
Funkcja przyjmuje wartość 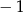 dla trzech różnych argumentów. dla trzech różnych argumentów. | P | F |
Funkcja przyjmuje wartość 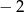 dla więcej niż 3 różnych argumentów. dla więcej niż 3 różnych argumentów. | P | F |
Dla argumentów z przedziału 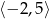 wartości funkcji są ujemne. wartości funkcji są ujemne. | P | F |
Dorota sporządziła z cukru i wody syrop do deseru. Stosunek masy cukru do masy wody w tym syropie jest równy 5 : 3. Ile procent masy tego syropu stanowi masa cukru?
A) 25% B) 37,5% C) 40% D) 60% E) 62,5%
Jacek sporządził z kwasku cytrynowego i wody roztwór czyszczący. Stosunek masy kwasku cytrynowego do masy wody w tym roztworze jest równy 2 : 23. Ile procent masy tego roztworu stanowi masa kwasku cytrynowego?
A) 92% B) 8,7% C) 8% D) 80% E) 4%
W pudełku znajduje się 30 losów loterii. 5 z tych losów jest wygrywających, 10 jest przegrywających, a wyciągnięcie jednego z pozostałych upoważnia do wyciągnięcia jeszcze jednego losu. Po wyciągnięciu los nie jest zwracany do pudełka. Pierwsza osoba, która brała udział w tej loterii, wyciągnęła los przegrywający.
Czy podane zdania są prawdziwe (P), czy fałszywe (F)?
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu wygrywającego wzrosło. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu przegrywającego zmalało. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu upoważniającego do ponownego losowania nie zmieniło się. | P | F |
Liczba 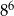 jest większa od liczby
jest większa od liczby 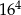
A) o 300% B) o 400% C) o 200% D) o 100%
Liczba 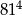 jest większa od liczby
jest większa od liczby 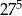
A) o 300% B) o 400% C) o 200% D) o 100%
Kwadrat 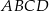 podzielono na 16 identycznych kwadratów (zobacz rysunek).
podzielono na 16 identycznych kwadratów (zobacz rysunek).
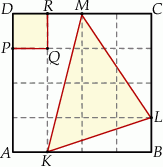
Jakim procentem pola kwadratu 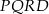 jest pole trójkąta
jest pole trójkąta 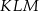 ?
?
A) 650% B) 600% C) 550% D) 500%
Liczby rzeczywiste  i
i 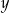 są dodatnie oraz
są dodatnie oraz 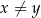 . Wyrażenie
. Wyrażenie 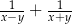 można przekształcić do postaci
można przekształcić do postaci
A) 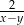 B)
B) 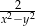 C)
C) 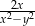 D)
D) 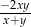
Liczby rzeczywiste  i
i 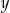 są dodatnie oraz
są dodatnie oraz 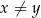 . Wyrażenie
. Wyrażenie 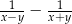 można przekształcić do postaci
można przekształcić do postaci
A) 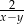 B)
B) 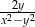 C)
C) 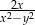 D)
D) 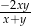
Ze zbioru liczb 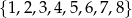 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 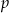 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 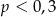 B)
B) 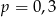 C)
C) 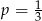 D)
D) 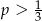
Ze zbioru liczb 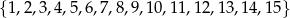 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 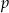 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 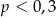 B)
B) 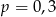 C)
C) 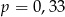 D)
D) 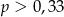
Ze zbioru 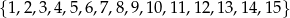 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 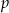 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
A) 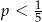 B)
B) 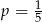 C)
C) 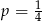 D)
D) 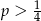
Ze zbioru liczb 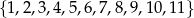 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 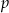 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 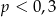 B)
B) 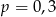 C)
C) 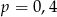 D)
D) 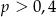
Ze zbioru liczb 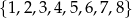 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 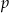 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 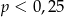 B)
B) 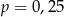 C)
C) 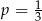 D)
D) 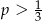
Na rysunku przedstawiono równoległobok 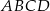 i trójkąt równoramienny
i trójkąt równoramienny 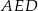 , w którym
, w którym 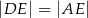 . Miara kąta
. Miara kąta 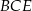 jest równa
jest równa 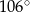 .
.
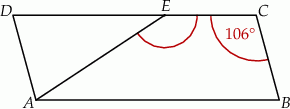
Jaką miarę ma kąt 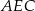 ?
?
A) 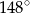 B)
B) 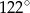 C)
C) 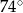 D)
D) 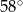
Na rysunku przedstawiono równoległobok 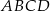 i trójkąt równoramienny
i trójkąt równoramienny 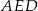 , w którym
, w którym 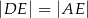 . Miara kąta
. Miara kąta 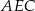 jest równa
jest równa 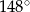 .
.
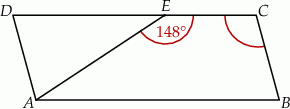
Jaką miarę ma kąt 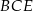 ?
?
A) 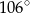 B)
B) 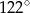 C)
C) 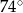 D)
D) 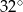
Dla 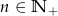 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A)  B)
B) 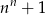 C)
C) 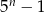 D)
D) 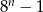
Dla 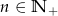 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A) 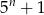 B)
B) 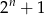 C)
C) 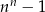 D)
D) 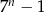
Dla 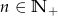 zawsze parzysta jest liczba
zawsze parzysta jest liczba
A) 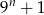 B)
B) 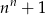 C)
C) 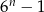 D)
D) 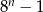
Średnia arytmetyczna pięciu liczb: 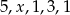 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 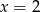 B)
B) 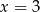 C)
C) 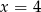 D)
D) 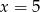
Średnia arytmetyczna zestawu danych: 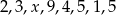 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że:
A) 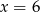 B)
B) 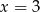 C)
C) 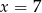 D)
D) 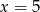
Średnia arytmetyczna pięciu liczb: 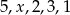 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 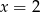 B)
B) 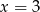 C)
C) 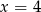 D)
D) 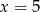
Średnia arytmetyczna pięciu liczb: 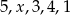 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 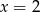 B)
B) 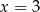 C)
C) 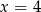 D)
D) 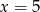
Średnia arytmetyczna siedmiu liczb: 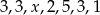 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 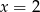 B)
B) 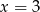 C)
C) 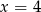 D)
D) 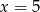
Średnia arytmetyczna dziesięciu liczb 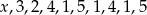 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 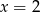 B)
B) 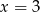 C)
C) 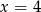 D)
D) 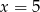
Średnia arytmetyczna ośmiu liczb: 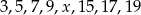 jest równa 11. Wtedy
jest równa 11. Wtedy
A) 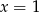 B)
B) 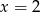 C)
C) 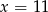 D)
D) 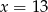
Średnia arytmetyczna sześciu liczb: 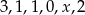 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Średnia arytmetyczna zestawu sześciu liczb: 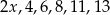 , jest równa 5. Wynika stąd, że
, jest równa 5. Wynika stąd, że
A) 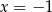 B)
B) 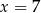 C)
C) 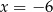 D)
D) 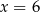
Średnia arytmetyczna pięciu liczb: 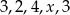 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy
A) 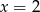 B)
B) 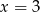 C)
C) 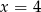 D)
D) 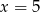
Dla jakiej wartości liczbowej  średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 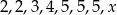 jest równa 4?
jest równa 4?
A) 6 B) 5 C) 4 D) 3
Średnia arytmetyczna zestawu danych: 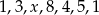 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że:
A) 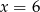 B)
B) 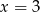 C)
C) 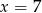 D)
D) 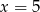
Średnia arytmetyczna liczb 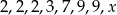 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa
A) 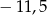 B) 1 C) 1,5 D) 2
B) 1 C) 1,5 D) 2
Średnia arytmetyczna dziesięciu liczb 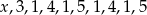 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 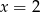 B)
B) 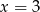 C)
C) 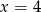 D)
D) 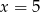
Średnia arytmetyczna liczb: 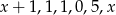 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A)  B) 2 C)
B) 2 C)  D)
D) 
Średnia arytmetyczna zestawu danych: 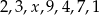 wynosi
wynosi 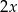 . Wynika z tego, że:
. Wynika z tego, że:
A) 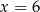 B)
B) 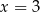 C)
C) 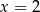 D)
D) 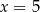
W układzie współrzędnych zaznaczono wierzchołki 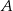 i
i 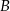 czworokąta
czworokąta 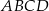 . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta.
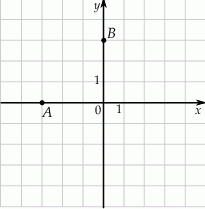
Pole czworokąta 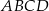 jest równe
jest równe
A) 9 B) 12 C) 18 D) 36
W układzie współrzędnych zaznaczono wierzchołki 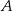 i
i 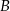 czworokąta
czworokąta  . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta.
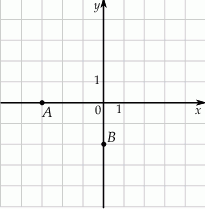
Pole czworokąta  jest równe
jest równe
A) 9 B) 12 C) 18 D) 36
W układzie współrzędnych zaznaczono wierzchołki  i
i 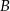 rombu
rombu 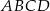 oraz jedną z jego osi symetrii.
oraz jedną z jego osi symetrii.
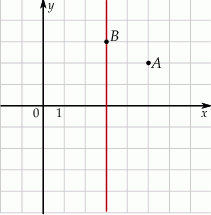
Pole rombu 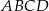 jest równe
jest równe
A) 2 B) 4 C) 6 D) 8
Funkcja 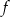 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 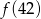 ,
, 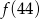 ,
, 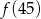 ,
, 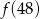 największa to
największa to
A) 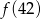 B)
B) 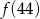 C)
C) 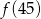 D)
D) 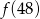
Funkcja 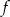 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 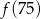 ,
, 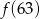 ,
, 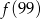 ,
, 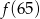 największa to
największa to
A) 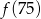 B)
B) 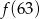 C)
C) 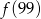 D)
D) 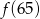
Dane są liczby: 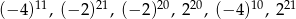 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wśród podanych liczb jest więcej liczb dodatnich, niż ujemnych. | P | F |
Wśród podanych liczb są 3 liczby równe 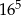 . . | P | F |
W pewnym zakładzie pracy w wyniku dwóch podwyżek zwiększono pensje pracowników o 26%. W ramach pierwszej z tych podwyżek płace zwiększono o 20%. O ile procent zwiększono płace w ramach drugiej podwyżki?
A) o 12% B) o 6% C) o 5% D) o 10%
W wyniku dwóch obniżek cenę komputera obniżono o 40%. Druga z tych obniżek była obniżką o 25%. O ile procent obniżono cenę komputera przy pierwszej obniżce?
A) o 15% B) o 65% C) o 20% D) o 30%
W wyniku dwóch obniżek cenę spodni obniżono o 52%. W ramach pierwszej z tych obniżek cenę zmniejszono o 20%. O ile procent zmniejszono cenę w ramach drugiej obniżki?
A) o 60% B) o 40% C) o 20% D) o 50%

