Równość 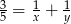 będzie prawdziwa, jeśli w miejsce
będzie prawdziwa, jeśli w miejsce  i
i 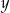 zostaną wpisane liczby
zostaną wpisane liczby
A) 5 i 2 B) 6 i 4 C) 10 i 2 D) 10 i 6
/Szkoła podstawowa/Zadania testowe
Równość 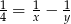 będzie prawdziwa, jeśli w miejsce
będzie prawdziwa, jeśli w miejsce  i
i 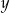 zostaną wpisane liczby
zostaną wpisane liczby
A) 3 i 15 B) 6 i 12 C) 3 i 6 D) 3 i 12
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
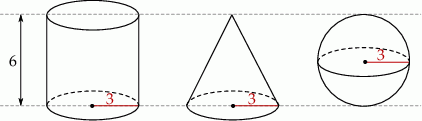
Na podstawie informacji przedstawionych na rysunku wybierz zdanie prawdziwe.
A) Objętość kuli jest większa od objętości walca.
B) Objętość stożka jest większa od objętości kuli.
C) Objętość walca jest 2 razy większa od objętości kuli.
D) Objętość stożka jest 3 razy mniejsza od objętości walca.
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
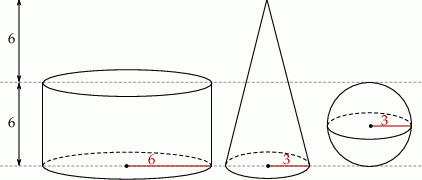
Na podstawie informacji przedstawionych na rysunku wybierz zdanie fałszywe.
A) Objętość kuli jest równa objętości stożka.
B) Objętość walca jest 3 razy większa od objętości stożka.
C) Objętość walca jest 6 razy większa od objętości kuli.
D) Suma objętości stożka i kuli jest mniejsza od objętości walca.
Na rysunku podano wymiary trzech pojemników w kształcie walca.
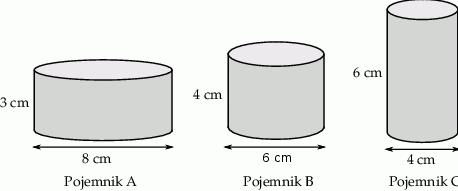
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość pojemnika 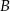 stanowi 70% objętości pojemnika stanowi 70% objętości pojemnika 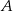 . . | P | F |
Objętość pojemnika 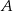 jest dwa razy większa od objętości pojemnika jest dwa razy większa od objętości pojemnika 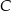 . . | P | F |
Suma kwadratów liczb 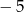 i
i 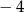 jest równa:
jest równa:
A) 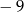 B) 81 C) 41 D)
B) 81 C) 41 D) 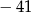
Liczba 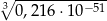 jest równa
jest równa
A) 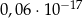 B)
B) 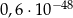 C)
C) 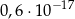 D)
D) 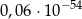
Liczba 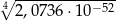 jest równa
jest równa
A) 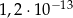 B)
B) 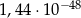 C)
C) 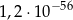 D)
D) 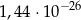
Dwa boki pewnego trójkąta mają długości 12 cm i 15 cm.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód tego trójkąta może być równy 28 cm. | P | F |
| Trzeci bok tego trójkąta może mieć długość 3 cm. | P | F |
Dwa boki pewnego trójkąta mają długości 14 cm i 11 cm.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Trzeci bok tego trójkąta może mieć długość 24 cm. | P | F |
| Obwód tego trójkąta może być równy 29 cm. | P | F |
Średnia arytmetyczna liczb: 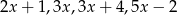 i
i 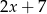 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 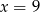 B)
B) 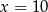 C)
C) 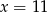 D)
D) 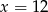
Średnia arytmetyczna liczb: 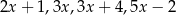 i
i 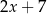 zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 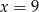 B)
B) 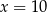 C)
C) 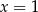 D)
D) 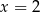
Średnia arytmetyczna liczb: 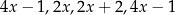 i
i 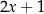 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 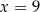 B)
B) 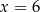 C)
C) 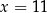 D)
D) 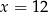
Ania ma w skarbonce 99 zł w monetach o nominałach 2 zł i 5 zł. Monet dwuzłotowych jest 2 razy więcej niż pięciozłotowych.
Jeżeli przez  oznaczymy liczbę monet pięciozłotowych, a przez
oznaczymy liczbę monet pięciozłotowych, a przez 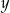 – liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
– liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
A) 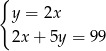 B)
B) 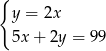 C)
C) 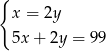 D)
D) 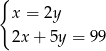
Tomek ma w skarbonce 156 zł w monetach o nominałach 2 zł i 5 zł. Monet dwuzłotowych jest 2 razy mniej niż pięciozłotowych.
Jeżeli przez  oznaczymy liczbę monet pięciozłotowych, a przez
oznaczymy liczbę monet pięciozłotowych, a przez 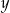 – liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
– liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
A) 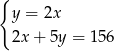 B)
B) 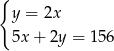 C)
C) 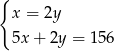 D)
D) 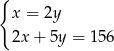
Piotrek ma w skarbonce  monet dwuzłotowych i
monet dwuzłotowych i 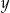 pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy mniej niż pięćdziesięciogroszówek, a wszystkie monety dają kwotę 36 złotych. Podane informacje przedstawia układ
pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy mniej niż pięćdziesięciogroszówek, a wszystkie monety dają kwotę 36 złotych. Podane informacje przedstawia układ
A) 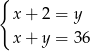 B)
B) 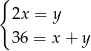 C)
C) 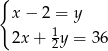 D)
D) 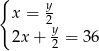
Piotrek ma w skarbonce  monet dwuzłotowych i
monet dwuzłotowych i 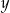 pięćdziesięciogroszówek. Dwuzłotówek jest o trzy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 52 złotych. Podane informacje przedstawia układ
pięćdziesięciogroszówek. Dwuzłotówek jest o trzy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 52 złotych. Podane informacje przedstawia układ
A) 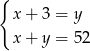 B)
B) 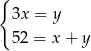 C)
C) 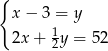 D)
D) 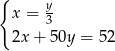
Piotrek ma w skarbonce  monet dwuzłotowych i
monet dwuzłotowych i 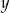 pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 27 złotych. Podane informacje przedstawia układ
pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 27 złotych. Podane informacje przedstawia układ
A) 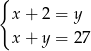 B)
B) 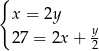 C)
C) 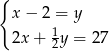 D)
D) 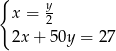
Która z liczb nie spełnia warunku 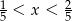 ?
?
A) 0,3 B) 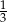 C)
C) 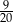 D)
D) 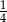
Na osi liczbowej zaznaczono punkty 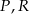 i
i 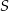 oraz podano współrzędne punktów
oraz podano współrzędne punktów 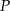 i
i 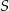 . Punkt
. Punkt 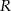 dzieli odcinek
dzieli odcinek 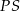 w taki sposób, że stosunek długości odcinków
w taki sposób, że stosunek długości odcinków 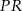 i
i 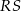 jest równy
jest równy  .
.
![]()
Współrzędna punktu 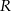 jest równa
jest równa
A) 21 B) 18 C) 16 D) 24
Trójkąt 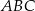 ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe
ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe 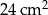 . Najdłuższa wysokość trójkąta
. Najdłuższa wysokość trójkąta 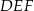 podobnego do trójkąta
podobnego do trójkąta 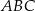 w skali 1:3 ma długość
w skali 1:3 ma długość
A) 4 cm B) 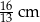 C) 2 cm D)
C) 2 cm D) 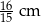
Odcinek 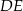 jest równoległy do podstawy
jest równoległy do podstawy 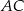 trójkąta równoramiennego
trójkąta równoramiennego 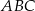 (zobacz rysunek).
(zobacz rysunek).
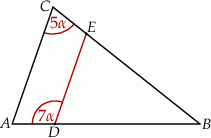
Kąt 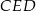 ma miarę A/B.
ma miarę A/B.
A) 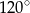 B)
B) 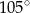
Kąt 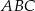 ma miarę C/D.
ma miarę C/D.
C) 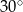 D)
D) 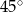
W układzie współrzędnych narysowano trapez równoramienny.
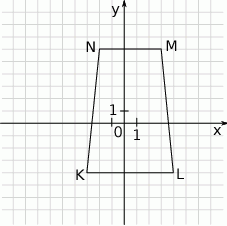
Równanie osi symetrii tego trapezu to
A) 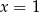 B)
B) 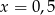 C)
C) 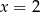 D)
D) 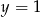
Na rysunku przedstawiono fragment podłogi pokrytej kaflami w kształcie kwadratów o boku długości 60 cm i kaflami w kształcie jednakowych prostokątów (patrz rysunek I). Na podłodze tej położono prostokątny dywan (patrz rysunek II).
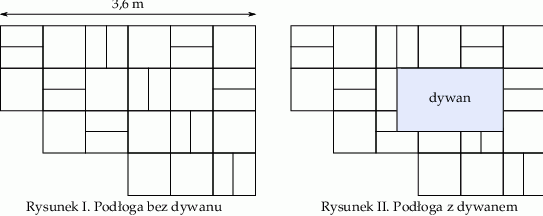
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dywan ma powierzchnię większą niż powierzchnia 4 kwadratowych kafli. | P | F |
Dywan ma wymiary 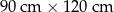 . . | P | F |
Na rysunku przedstawiono fragment podłogi pokrytej kaflami w kształcie kwadratów i kaflami w kształcie jednakowych prostokątów (patrz rysunek I). Na podłodze tej położono prostokątny dywan (patrz rysunek II).
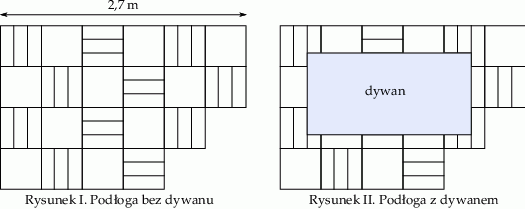
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dywan ma pole powierzchni większe niż 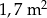 | P | F |
Dywan ma wymiary 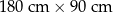 . . | P | F |
Liczbą większą od 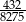 jest
jest
A) 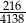 B)
B) 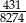 C)
C) 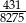 D)
D) 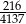
Liczba ścian ostrosłupa prawidłowego jest o 5 mniejsza niż liczba jego krawędzi. Pole powierzchni całkowitej tego ostrosłupa jest równe 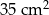 , a pole podstawy jest równe
, a pole podstawy jest równe 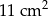 . Pole jednej ściany bocznej tego ostrosłupa jest równe
. Pole jednej ściany bocznej tego ostrosłupa jest równe
A) 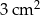 B)
B) 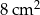 C)
C) 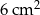 D)
D) 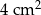
Długość przekątnej 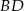 deltoidu przedstawionego na rysunku jest równa
deltoidu przedstawionego na rysunku jest równa
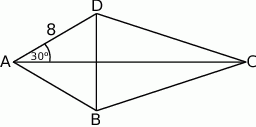
A) 9 B) 8 C) 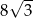 D)
D) 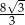
Liczba 1450 jest zaokrągleniem do rzędu dziesiątek kilku liczb naturalnych. Ile jest wszystkich liczb naturalnych różnych od 1450, które mają takie zaokrąglenie?
A) 4 B) 5 C) 9 D) 10
Liczba 15000 jest zaokrągleniem do rzędu dziesiątek kilku liczb naturalnych. Ile jest wszystkich liczb naturalnych różnych od 15000, które mają takie zaokrąglenie?
A) 9 B) 10 C) 99 D) 100
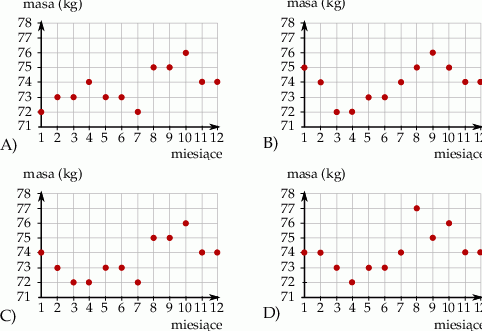
W pierwszym dniu każdego miesiąca ubiegłego roku pan Tomek zapisywał masę swojego ciała. Początkowo masa jego ciała malała. W listopadzie i grudniu ważył tyle samo, ile w lipcu. W żadnym miesiącu nie ważył więcej niż 76 kg. Pan Tomek wyniki swoich pomiarów umieścił na diagramie.
Który z diagramów przedstawia wyniki pomiarów pana Tomka w ubiegłym roku?
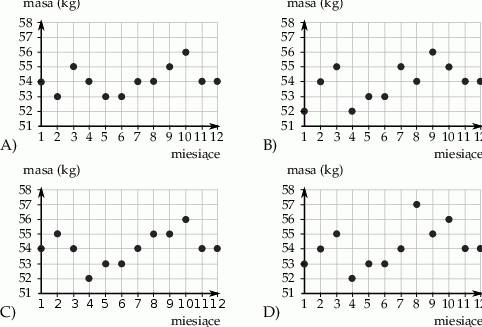
W ostatnim dniu każdego miesiąca ubiegłego roku pani Urszula zapisywała masę swojego ciała. Początkowo masa jej ciała rosła. W lipcu ważyła tylko samo, ile w listopadzie i mniej niż w marcu. W żadnym miesiącu nie ważyła mniej niż 52 kg. Pani Urszula wyniki swoich pomiarów umieściła na diagramie.
Który z diagramów przedstawia wyniki pomiarów pani Urszuli w ubiegłym roku?
Wykres przedstawia zmianę temperatury powietrza oraz temperatury odczuwalnej w ciągu doby (temperatura odczuwalna jest nieco niższa niż temperatura rzeczywista ponieważ uwzględnia wiatr i spowodowane nim uczucie chłodu).
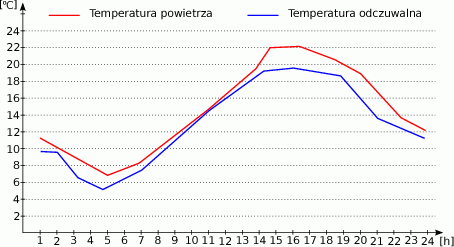
Jaka była różnica między temperaturą rzeczywistą, a odczuwalną o godzinie 20:00?
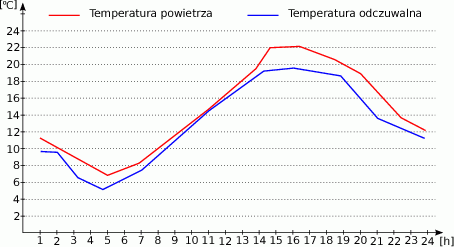
A)
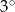 B)
B) 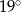 C)
C) 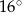 D)
D) 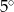
Wykres przedstawia zmianę temperatury powietrza oraz temperatury odczuwalnej w ciągu doby (temperatura odczuwalna jest nieco niższa niż temperatura rzeczywista ponieważ uwzględnia wiatr i spowodowane nim uczucie chłodu).
O ile stopni wzrosła temperatura odczuwalna w godzinach 9:00 – 12:00?
A)
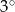 B)
B) 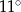 C)
C) 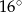 D)
D) 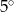
Wykres przedstawia zmianę temperatury powietrza oraz temperatury odczuwalnej w ciągu doby (temperatura odczuwalna jest nieco niższa niż temperatura rzeczywista ponieważ uwzględnia wiatr i spowodowane nim uczucie chłodu).
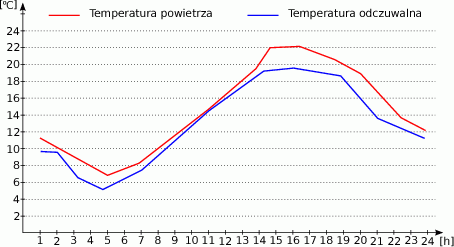
Jak długo rzeczywista temperatura powietrza była wyższa niż
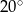 ?
?A) przez 3 godziny B) przez 5 godzin C) przez 4 godziny D) przez 6 godzin
Która z liczb nie może być średnią arytmetyczną liczby uczniów w czterech klasach trzecich?
A) 23,4 B) 25,5 C) 27,25 D) 21,75

