Na treningu odmierzano za pomocą aplikacji komputerowej 15–minutowe cykle ćwiczeń, które następowały bezpośrednio jeden po drugim. Ola zaczęła ćwiczyć, gdy pierwszy cykl trwał już 2 minuty, a skończyła, gdy do końca trzeciego cyklu zostało jeszcze 7 minut. Ile łącznie minut Ola ćwiczyła na zajęciach?
A) 36 B) 35 C) 24 D) 21
/Szkoła podstawowa/Zadania testowe
W trójkącie 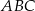 największą miarę ma kąt przy wierzchołku
największą miarę ma kąt przy wierzchołku 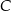 . Miara kąta przy wierzchołku
. Miara kąta przy wierzchołku 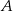 jest równa
jest równa 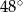 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 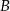 jest równa różnicy miary kąta przy wierzchołku
jest równa różnicy miary kąta przy wierzchołku 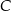 oraz miary kąta przy wierzchołku
oraz miary kąta przy wierzchołku 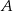 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt przy wierzchołku 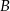 ma miarę ma miarę 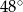 . . | P | F |
Trójkąt 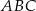 jest prostokątny. jest prostokątny. | P | F |
W trójkącie 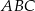 najmniejszą miarę ma kąt przy wierzchołku
najmniejszą miarę ma kąt przy wierzchołku 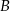 . Miara kąta przy wierzchołku
. Miara kąta przy wierzchołku 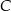 jest równa
jest równa 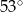 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 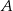 jest równa sumie miary kąta przy wierzchołku
jest równa sumie miary kąta przy wierzchołku 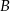 oraz miary kąta przy wierzchołku
oraz miary kąta przy wierzchołku 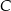 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt przy wierzchołku 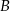 ma miarę ma miarę 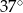 . . | P | F |
Trójkąt 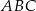 jest ostrokątny. jest ostrokątny. | P | F |
Ze zbioru 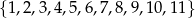 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 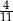 B)
B) 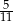 C)
C) 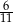 D)
D) 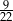
Ze zbioru liczb 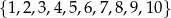 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru 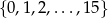 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 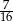 B)
B)  C)
C) 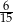 D)
D) 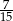
Ze zbioru 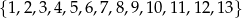 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 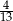 B)
B) 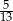 C)
C) 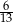 D)
D) 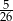
Jacek i Ola testują swoje elektryczne deskorolki. W tym celu zmierzyli czasy przejazdu na trasie 400 m. Ola pokonała tę trasę w czasie 160 s, a Jacek – w czasie 100 s. Różnica średnich prędkości uzyskanych przez Jacka i przez Olę jest równa
A) 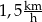 B)
B) 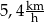 C)
C) 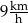 D)
D) 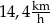
Amelia i Jakub testują swoje elektryczne hulajnogi. W tym celu zmierzyli czasy przejazdu na trasie 600 m. Amelia pokonała tę trasę w czasie 180 s, a Jakub – w czasie 144 s. Różnica średnich prędkości uzyskanych przez Jakuba i przez Amelię jest równa
A) 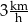 B)
B) 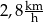 C)
C) 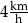 D)
D) 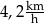
Dane są cztery wyrażenia:
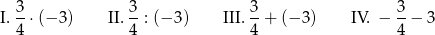
Największą wartość ma wyrażenie
A) I B) II C) III D) IV
Dane są cztery wyrażenia:
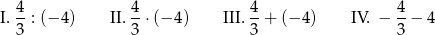
Największą wartość ma wyrażenie
A) I B) II C) III D) IV
Dane są cztery liczby 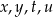 zapisane za pomocą wyrażeń arytmetycznych:
zapisane za pomocą wyrażeń arytmetycznych:
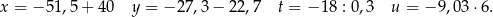
Która z tych liczb jest największa?
A)  B)
B) 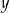 C)
C) 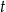 D)
D) 
Dane są cztery liczby 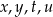 zapisane za pomocą wyrażeń arytmetycznych:
zapisane za pomocą wyrażeń arytmetycznych:
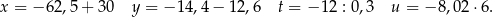
Która z tych liczb jest największa?
A)  B)
B) 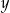 C)
C) 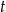 D)
D) 
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 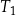 i
i 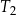 oraz podano długości ich boków.
oraz podano długości ich boków.
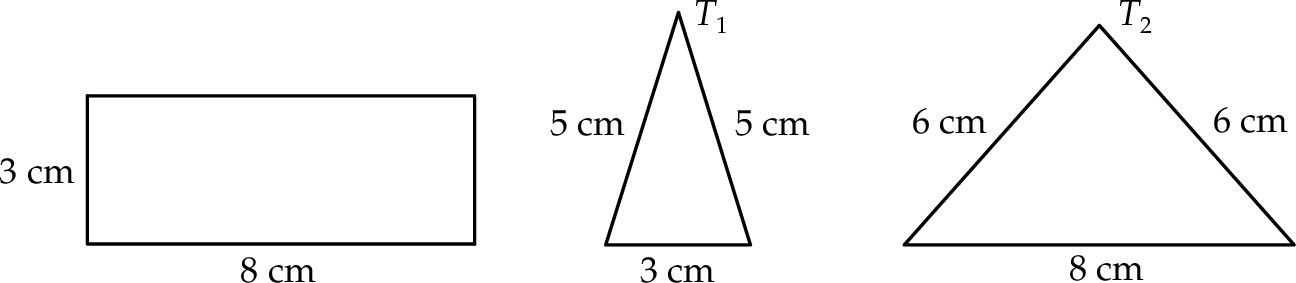
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów 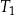 i i 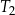 . . |
| B) | trójkąty 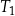 i i 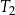 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkąta 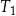 mają inną długość niż ramiona trójkąta mają inną długość niż ramiona trójkąta 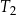 . . |
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 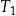 i
i 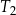 oraz podano długości ich boków.
oraz podano długości ich boków.
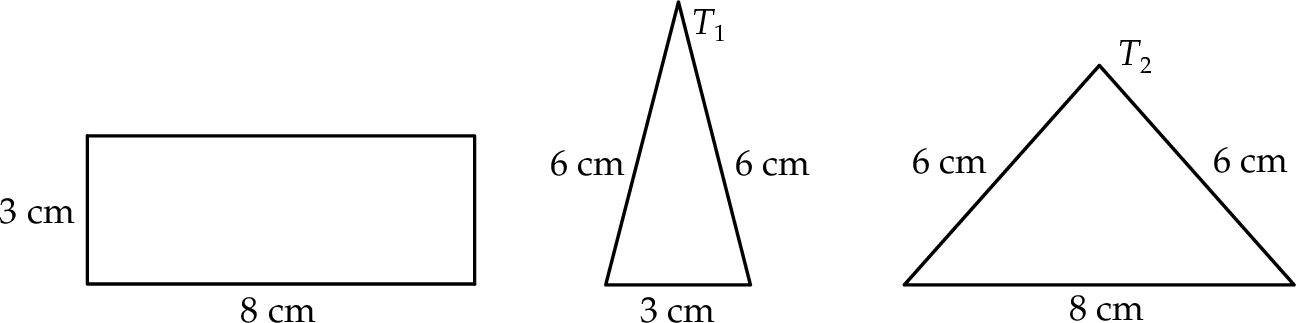
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów 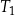 i i 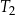 . . |
| B) | trójkąty 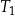 i i 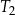 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkątów 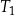 i i 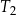 nie są równe długościom boków prostokąta. nie są równe długościom boków prostokąta. |
Siatka ostrosłupa składa się z kwadratu i czterech trójkątów prostokątnych zbudowanych na bokach tego kwadratu.
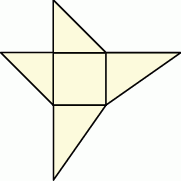
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wysokość tego ostrosłupa jest równa długości jednej z jego krawędzi. | P | F |
| Wszystkie wysokości ścian bocznych tego ostrosłupa mają taką samą długość. | P | F |
Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 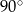 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
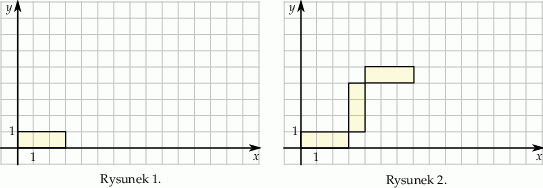
Marcel narysował w ten sposób pięć prostokątów. Współrzędna
 prawego górnego wierzchołka piątego prostokąta jest równa
prawego górnego wierzchołka piątego prostokąta jest równaA) 11 B) 10 C) 9 D) 8
Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 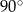 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
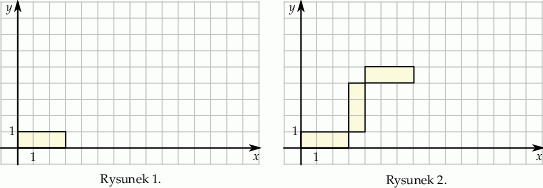
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli punkt
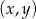 jest prawym górnym wierzchołkiem 20 prostokąta to
jest prawym górnym wierzchołkiem 20 prostokąta to 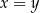 | P | F |
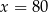 | P | F |
Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 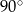 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
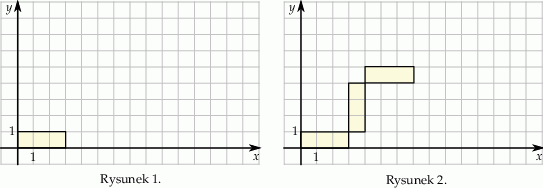
Współrzędne prawego górnego wierzchołka 39 prostokąta są równe
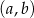 . Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe
. Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe A)
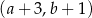 B)
B) 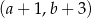 C)
C) 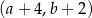 D)
D) 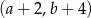
Badając pewien roztwór stwierdzono, że zawiera on 0,05 g chloru, co stanowi 0,02% masy roztworu. Jaka była masa roztworu?
A) 2,5 kg B) 250 g C) 25 g D) 2,5 g
Badając pewien roztwór stwierdzono, że zawiera on 0,06 g chloru, co stanowi 0,04% masy roztworu. Jaka była masa roztworu?
A) 1,5 kg B) 15 g C) 150 g D) 1,5 g
Badając pewien roztwór stwierdzono, że zawiera on 0,05 g chloru, co stanowi 0,01% masy roztworu. Jaka była masa roztworu?
A) 5 kg B) 50 g C) 500 g D) 5 g
Liczby  i
i 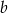 są dwucyfrowe oraz liczba
są dwucyfrowe oraz liczba 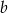 powstaje z
powstaje z  w wyniku zapisania cyfr liczby
w wyniku zapisania cyfr liczby  w odwrotnej kolejności. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
w odwrotnej kolejności. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 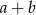 jest zawsze podzielna przez 11. jest zawsze podzielna przez 11. | P | F |
Liczba 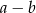 jest zawsze podzielna przez 9. jest zawsze podzielna przez 9. | P | F |
Cenę laptopa obniżono najpierw o 200 zł, a następnie cenę obniżono o 30%. Po tych dwóch obniżkach pani Kasia kupiła tego laptopa za 1750 zł. Jaka była cena laptopa przed obniżkami?
A) 2500 zł. B) 2400 zł. C) 2700 zł. D) 2785 zł.
Dana jest liczba 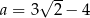 .
.
Liczba o 2 większa od liczby  jest równa A/B.
jest równa A/B.
A) 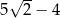 B)
B) 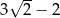
Liczba 2 razy większa od liczby  jest równa C/D.
jest równa C/D.
C) 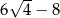 D)
D) 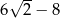
Dana jest liczba 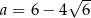 .
.
Liczba o 2 mniejsza od połowy liczby  jest równa A/B.
jest równa A/B.
A) 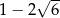 B)
B) 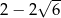
Połowa liczby o 2 większej od  równa C/D.
równa C/D.
C) 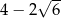 D)
D) 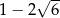
Pole powierzchni pokoju jest równe 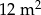 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
A) 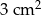 B)
B) 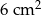 C)
C) 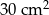 D)
D) 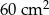
Pole działki budowlanej jest równe 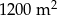 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 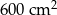 B)
B) 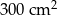 C)
C) 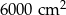 D)
D) 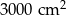
Pole powierzchni pokoju jest równe 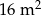 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
A) 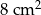 B)
B) 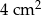 C)
C) 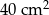 D)
D) 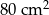
Pole działki budowlanej jest równe 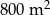 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 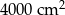 B)
B) 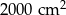 C)
C) 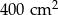 D)
D) 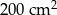
Pole powierzchni pokoju jest równe 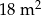 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:300 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:300 wynosi:
A) 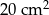 B)
B) 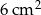 C)
C) 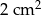 D)
D) 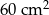
Sprzedawca kupił do swojego sklepu 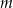 kilogramów marchwi i
kilogramów marchwi i 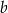 kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
A) 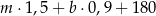 B)
B) 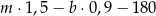
C) 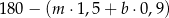 D)
D) 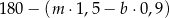
Sprzedawca sprzedał w swoim sklepie 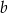 kilogramów bananów i
kilogramów bananów i 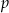 kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
A) 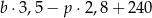 B)
B) 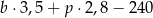
C) 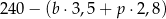 D)
D) 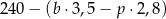
Właściciel sklepu przemysłowego kupił  opakowań 5-kilogramowego proszku do prania w cenie
opakowań 5-kilogramowego proszku do prania w cenie  złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu?
złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu?
A) 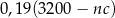 B)
B) 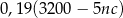
C) 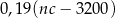 D)
D) 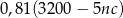
Sprzedawca kupił od ogrodnika róże i tulipany za łączną kwotę 580 zł. Jeden tulipan kosztował 1,20 zł, a cena jednej róży była równa 4 zł. Sprzedawca kupił o 50 tulipanów więcej niż róż. Jeśli liczbę zakupionych tulipanów oznaczymy przez 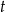 , to podane zależności opisuje równanie
, to podane zależności opisuje równanie
A) 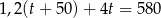 B)
B) 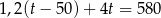
C) 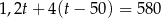 D)
D) 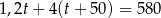
Jeden litr to 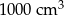 . Jeden metr sześcienny to
. Jeden metr sześcienny to
A) 100 litrów B) 1000 litrów C) 10000 litrów D) 10 litrów
Jeden litr to 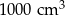 . Jeden metr sześcienny to A/B litrów.
. Jeden metr sześcienny to A/B litrów.
A) 10000 B) 1000
Jeden  to C/D litra.
to C/D litra.
C) 0,0001 D) 0,000001
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
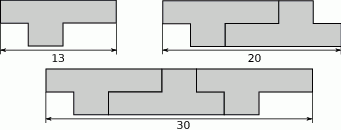
Ułożono wzór z 4 płytek, jak na rysunku.

Odcinek  ma długość
ma długość
A) 43 cm B) 37 cm C) 40 cm D) 46 cm
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
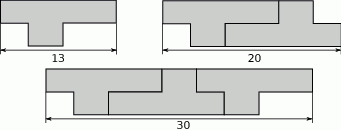
Ułożono wzór z 7 płytek, jak na rysunku.

Odcinek  ma długość
ma długość
A) 64 cm B) 68 cm C) 60 cm D) 73 cm
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
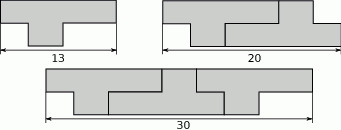
Niech  będzie całkowitą szerokością wzoru ułożonego z
będzie całkowitą szerokością wzoru ułożonego z  płytek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
płytek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli 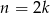 jest liczbą parzystą, to jest liczbą parzystą, to 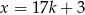 . . | P | F |
Jeżeli 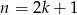 jest liczbą nieparzystą, to jest liczbą nieparzystą, to 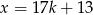 | P | F |
Na czas trwania promocji obniżono ceny niektórych produktów odzieżowych.
| Produkt | Stara cena | Nowa cena |
| Spodnie | 150 zł | niższa o 30% |
| Kurtka | 165 zł | 99 zł |
| Spódnica | 133 zł (niższa o 30%) | |
| Koszula | 120 zł | 96 zł |
A) spodni B) kurtki C) spódnicy D) koszuli
Na czas trwania promocji obniżono ceny niektórych produktów odzieżowych.
| Produkt | Stara cena | Nowa cena |
| Spodnie | 150 zł | niższa o 30% |
| Kurtka | 165 zł | 99 zł |
| Spódnica | 133 zł (niższa o 30%) | |
| Koszula | 120 zł | 96 zł |
| Przed obniżką najtańsza była spódnica. | P | F |
| Po obniżce najtańsze są spodnie. | P | F |
Na czas trwania promocji obniżono ceny niektórych produktów odzieżowych.
| Produkt | Stara cena | Nowa cena |
| Spodnie | 150 zł | niższa o 30% |
| Kurtka | 165 zł | 99 zł |
| Spódnica | 133 zł (niższa o 30%) | |
| Koszula | 120 zł | 96 zł |
A) spodni B) kurtki C) spódnicy D) koszuli
W prostokącie 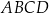 punkty
punkty 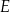 i
i 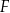 są środkami boków
są środkami boków 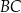 i
i 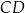 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 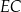 jest równa 6 cm, a długość odcinka
jest równa 6 cm, a długość odcinka 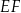 jest równa 10 cm.
jest równa 10 cm.

Obwód prostokąta 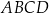 jest równy
jest równy
A) 64 cm B) 56 cm C) 40 cm D) 28 cm
W prostokącie 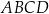 punkty
punkty 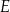 i
i 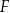 są środkami boków
są środkami boków 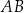 i
i 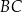 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 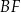 jest równa 9 cm, a długość odcinka
jest równa 9 cm, a długość odcinka 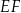 jest równa 15 cm.
jest równa 15 cm.
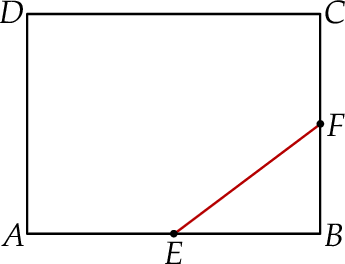
Obwód prostokąta 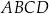 jest równy
jest równy
A) 84 cm B) 96 cm C) 60 cm D) 72 cm
Równość 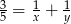 będzie prawdziwa, jeśli w miejsce
będzie prawdziwa, jeśli w miejsce  i
i 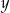 zostaną wpisane liczby
zostaną wpisane liczby
A) 5 i 2 B) 6 i 4 C) 10 i 2 D) 10 i 6
Równość 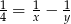 będzie prawdziwa, jeśli w miejsce
będzie prawdziwa, jeśli w miejsce  i
i 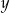 zostaną wpisane liczby
zostaną wpisane liczby
A) 3 i 15 B) 6 i 12 C) 3 i 6 D) 3 i 12
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
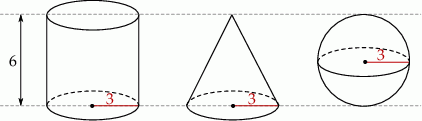
Na podstawie informacji przedstawionych na rysunku wybierz zdanie prawdziwe.
A) Objętość kuli jest większa od objętości walca.
B) Objętość stożka jest większa od objętości kuli.
C) Objętość walca jest 2 razy większa od objętości kuli.
D) Objętość stożka jest 3 razy mniejsza od objętości walca.
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
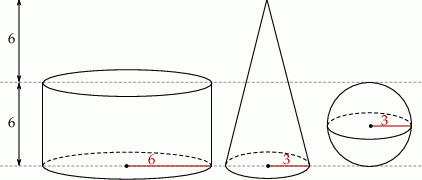
Na podstawie informacji przedstawionych na rysunku wybierz zdanie fałszywe.
A) Objętość kuli jest równa objętości stożka.
B) Objętość walca jest 3 razy większa od objętości stożka.
C) Objętość walca jest 6 razy większa od objętości kuli.
D) Suma objętości stożka i kuli jest mniejsza od objętości walca.
Na rysunku podano wymiary trzech pojemników w kształcie walca.
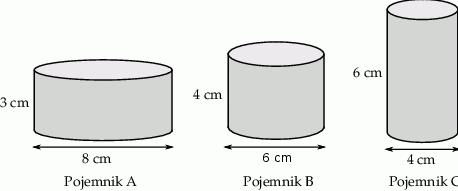
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość pojemnika 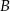 stanowi 70% objętości pojemnika stanowi 70% objętości pojemnika 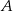 . . | P | F |
Objętość pojemnika 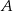 jest dwa razy większa od objętości pojemnika jest dwa razy większa od objętości pojemnika 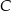 . . | P | F |

