Punkty 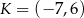 i
i 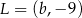 są końcami odcinka
są końcami odcinka 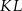 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 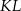 jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
A) 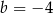 B)
B) 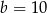 C)
C) 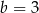 D)
D) 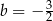
/Szkoła podstawowa/Zadania testowe
Dane są liczby: 2000, 16000, 32000. Iloczyn tych liczb jest równy
A) 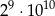 B)
B) 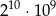 C)
C) 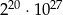 D)
D) 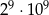
W pewnej loterii przygotowano 20 losów wygrywających i pewną liczbę losów przegrywających. W trakcie losowania wyciągnięto 20 losów i wszystkie były przegrywające. Po wyciągnięciu tych 20 losów prawdopodobieństwo wyciągnięcia losu wygrywającego wzrosło do 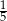 . Na loterię przygotowano A/B losów przegrywających.
. Na loterię przygotowano A/B losów przegrywających.
A) 80 B) 100
Wyciągnięto kolejnych 10 losów przegrywających. Zatem prawdopodobieństwo wyciągnięcia losu wygrywającego wzrosło do C/D.
C) 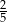 D)
D) 
W naczyniu znajdowało się 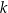 litrów wody. Marcin odlał z tego naczynia
litrów wody. Marcin odlał z tego naczynia 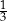 tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
A) 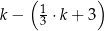 B)
B) 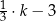 C)
C) 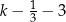 D)
D) 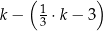
Wykonano następującą konstrukcję.
1. Narysowano romb 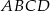 .
.
2. Wykreślono przekątne rombu i ich punkt przecięcia oznaczono literą  .
.
3. Poprowadzono prostą prostopadłą do boku 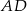 i przechodzącą przez punkt
i przechodzącą przez punkt 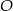 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 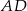 oznaczono literą
oznaczono literą 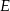 .
.
4. Narysowano okrąg o środku w punkcie 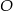 i promieniu
i promieniu 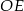 .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego rombu.
B) jest styczny do wszystkich boków tego rombu.
C) jest styczny do przekątnych tego rombu.
D) nie ma punktów wspólnych z jednym z boków rombu.
Prosta 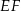 dzieli prostokąt
dzieli prostokąt 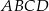 na kwadrat
na kwadrat 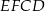 o obwodzie 32 cm i prostokąt
o obwodzie 32 cm i prostokąt 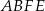 o obwodzie o 6 cm mniejszym od obwodu kwadratu
o obwodzie o 6 cm mniejszym od obwodu kwadratu  .
.
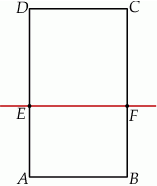
Długość odcinka  jest równa
jest równa
A) 2 cm B) 4 cm C) 5 cm D) 8 cm
Na rysunku przedstawiono graniastosłup prosty trójkątny oraz jego podstawę. Wysokość tego graniastosłupa jest równa 1 cm.

Pole powierzchni bocznej tego graniastosłupa jest A/B pole jednej podstawy.
A) takie samo jak B) dwa razy większe niż
Pole powierzchni całkowitej tego graniastosłupa jest równe C/D.
C) 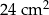 D)
D) 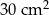
Promień kuli jest równy promieniowi podstawy walca, oraz objętości obu brył są równe. Stosunek pola powierzchni kuli do pola powierzchni całkowitej walca jest równy
A) 1 B)  C)
C) 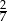 D)
D) 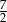
Dana jest liczba dwucyfrowa. W tej liczbie cyfrą dziesiątek jest  , cyfrą jedności jest
, cyfrą jedności jest 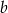 oraz spełnione są warunki:
oraz spełnione są warunki: 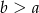 i
i 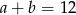 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Warunki zadania spełnia siedem liczb. | P | F |
| Wszystkie liczby spełniające warunki zadania są podzielne przez 3. | P | F |
Dana jest liczba trzycyfrowa. W tej liczbie cyfrą setek jest  , cyfrą dziesiątek jest
, cyfrą dziesiątek jest 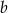 , cyfrą jedności jest
, cyfrą jedności jest  oraz spełnione są warunki:
oraz spełnione są warunki: 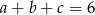 ,
, 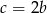 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Warunki zadania spełniają dwie liczby. | P | F |
| Wszystkie liczby spełniające warunki zadania są podzielne przez 24. | P | F |
Dana jest liczba dwucyfrowa. W tej liczbie cyfrą dziesiątek jest  , cyfrą jedności jest
, cyfrą jedności jest 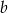 oraz spełnione są warunki:
oraz spełnione są warunki: 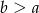 i
i 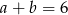 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Warunki zadania spełniają dwie liczby. | P | F |
| Wszystkie liczby spełniające warunki zadania są podzielne przez 6. | P | F |
Zuzanna wybrała się na 14–kilometrową pieszą wycieczkę. Trasa wycieczki składała się z dwóch etapów, pomiędzy którymi Zuzanna zrobiła przerwę śniadaniową. Na wykresie przedstawiono jak zmieniała się w czasie odległość Zuzanny od miejsca rozpoczęcia wycieczki.
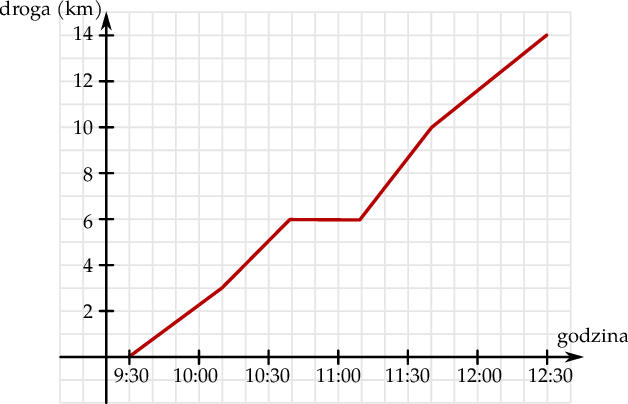
Średnia prędkość z jaką Zuzanna pokonała drugi etap wycieczki jest równa A/B.
A) 6 km/h B) 8 km/h
Przerwa śniadaniowa zajęła C/D całego czasu poświęconego na wycieczkę.
C) 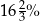 D)
D) 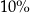
Basen ogrodowy, o wymiarach podanych na rysunku, wypełniono wodą do  jego wysokości.
jego wysokości.
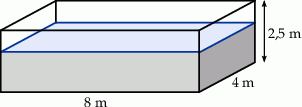
Ile litrów wody jest w basenie?
A) 48 000 litrów B) 480 000 litrów C) 4 800 litrów D) 480 litrów
Skrzynia ma kształt prostopadłościanu. Podłoga skrzyni ma wymiary 2,4 m i 1,5 m, a wysokość skrzyni jest równa 1 m. Piasek wsypany do skrzyni zajmuje  jej pojemności. Ile metrów sześciennych piasku wsypano do skrzyni?
jej pojemności. Ile metrów sześciennych piasku wsypano do skrzyni?
A) 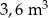 B)
B) 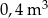 C)
C) 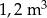 D)
D) 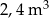
Skrzynia ma kształt prostopadłościanu. Podłoga skrzyni ma wymiary 1,5 m i 1,2 m, a wysokość skrzyni jest równa 1 m. Piasek wsypany do skrzyni zajmuje  jej pojemności. Ile metrów sześciennych piasku wsypano do skrzyni?
jej pojemności. Ile metrów sześciennych piasku wsypano do skrzyni?
A) 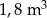 B)
B) 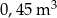 C)
C) 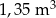 D)
D) 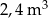
Ewa z sześciennych klocków o krawędzi długości 3 cm skleiła kilka brył o kształcie pokazanym na rysunku.
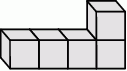
Z czterech takich brył Ewa skleiła graniastosłup prawidłowy czworokątny. Wysokość tego graniastosłupa jest równa A/B.
A) 12 cm B) 15 cm
Pole powierzchni bocznej utworzonego graniastosłupa jest równe C/D.
C) 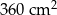 D)
D) 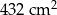
Każda z dwóch wind towarowych obsługujących nowo budowany wieżowiec porusza się z prędkością 1,2 km/h. Na schemacie zaznaczono niektóre długości trasy pokonywanej przez windy.
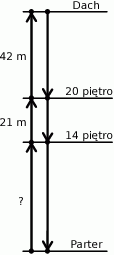
Jak długo trwa przejazd windy między dachem, a 14 piętrem?
A) 3 minuty B) 3 minuty i 9 sekund C) 6 minut i 18 sekund D) 4 minuty
Każda z dwóch wind towarowych obsługujących nowo budowany wieżowiec porusza się z prędkością 1,2 km/h. Na schemacie zaznaczono niektóre długości trasy pokonywanej przez windy.
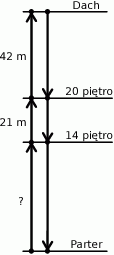
Winda zaczyna zjeżdżać z dachu o 1 minutę i 24 sekundy później niż winda wyjeżdżająca z parteru. Obie windy w tym samym momencie dojeżdżają do 20 piętra. Długość trasy windy pomiędzy parterem, a 14 piętrem jest równa
A) 49 metrów B) 42 metry C) 36 metrów D) 52 metry
Na siatce sześcianu zaznaczono jego dwie ściany 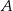 i
i 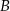 oraz jego dwie krawędzie
oraz jego dwie krawędzie 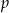 i
i 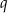 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ściany  i i  są przeciwległymi ścianami sześcianu. są przeciwległymi ścianami sześcianu. | P | F |
Krawędzie 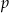 i i 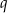 są prostopadłymi krawędziami sześcianu. są prostopadłymi krawędziami sześcianu. | P | F |
Liczba  jest największą liczbą dwucyfrową podzielną przez 2 i 3, a liczba
jest największą liczbą dwucyfrową podzielną przez 2 i 3, a liczba 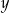 jest największą liczbą trzycyfrową o trzech różnych cyfrach parzystych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest największą liczbą trzycyfrową o trzech różnych cyfrach parzystych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Największy wspólny dzielnik liczb  i i 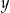 jest równy 96. jest równy 96. | P | F |
Najmniejsza wspólna wielokrotność liczb  i i 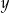 jest równa 864. jest równa 864. | P | F |
Ośrodek pomocy społecznej przyznał zapomogę grupie kilkudziesięciu osób. Świadczenie zostało wypłacone w dwóch wysokościach: 25% osób otrzymało zapomogę w wysokości 560 zł, a pozostałe osoby otrzymały zapomogę w wyższej kwocie. Średnia arytmetyczna wypłaconych świadczeń wyniosła 605 zł. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wyższa kwota zapomogi była równa 620 zł. | P | F |
| Gdyby niższą kwotę zapomogi obniżyć o 50 zł, a wyższą kwotę zapomogi podnieść o 50 zł, to średnia wypłaconych świadczeń nie uległaby zmianie. | P | F |
Cenę pewnego towaru obniżono najpierw o 30%, a potem jeszcze o 50%.
O ile procent cena po obniżkach jest niższa od ceny początkowej?
A) 65% B) 80% C) 35% D) 70%
W pewnym opakowaniu są płatki owsiane z rodzynkami. Masa zawartości tego opakowania jest równa 320 g, przy czym 15% tej masy stanowią rodzynki. Ola zmieszała całą zawartość tego opakowania z 80 g orzechów. W mieszance przygotowanej przez Olę masa orzechów jest większa o A/B od masy rodzynek.
A) 32 g B) 48 g
Mieszanka przygotowana przez Olę zawiera C/D orzechów.
C) 20% D) 25%
Zuzia dojeżdża do szkoły autobusem linii 121. Droga z domu na przystanek zajmuje jej 7 minut, podróż autobusem trwa 14 minut, a czas dojścia do szkoły od przystanku zajmuje jej 12 minut. W tabeli zamieszczono fragment rozkładu jazdy autobusu linii 121, którym Zuzia dojeżdża do szkoły.
| Godzina | Minuty |
| 6 | 04 12 20 28 36 44 52 |
| 7 | 00 08 16 24 32 40 48 56 |
| 8 | 04 12 20 28 36 44 52 |
| 9 | 00 08 16 24 32 40 48 56 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli Zuzia wyjdzie z domu o godz. 7:35, to będzie w szkole przed 8:15. | P | F |
| Jeżeli Zuzia dotarła do szkoły przed godz. 9:33, to wyszła z domu przed 8:55. | P | F |
Punkt 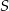 jest środkiem okręgu wpisanego w romb
jest środkiem okręgu wpisanego w romb 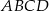 . Okrąg ten jest styczny do boku
. Okrąg ten jest styczny do boku 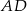 w punkcie
w punkcie 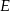 oraz
oraz 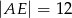 ,
, 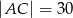 .
.
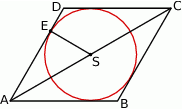
Promień  okręgu ma długość
okręgu ma długość
A) 12 B) 9 C) 8 D) 6

