Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
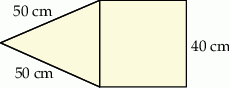
Suma długości wszystkich krawędzi tego ostrosłupa jest równa
A) 560 cm B) 360 cm C) 260 cm D) 220 cm
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.

Suma długości wszystkich krawędzi tego ostrosłupa jest równa
A) 560 cm B) 360 cm C) 260 cm D) 220 cm
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego trójkątnego.
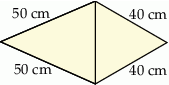
Suma długości wszystkich krawędzi tego ostrosłupa jest równa
A) 560 cm B) 360 cm C) 260 cm D) 270 cm
Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa 450. Krawędź boczna jest w tym ostrosłupie czterokrotnie dłuższa od krawędzi podstawy.
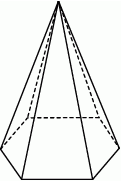
Długość krawędzi podstawy tego ostrosłupa jest równa
A) 15 B) 25 C) 50 D) 60
Suma długości wszystkich krawędzi ostrosłupa prawidłowego sześciokątnego jest równa 540. Krawędź boczna jest w tym ostrosłupie pięciokrotnie dłuższa od krawędzi podstawy.
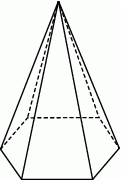
Długość krawędzi podstawy tego ostrosłupa jest równa
A) 15 B) 25 C) 50 D) 60
Rysunek przedstawia ostrosłup prosty.
Oceń, czy podane zdania są prawdziwe. Zaznacz P (prawda) lub F (fałsz).
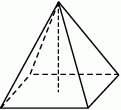
| Ściany boczne ostrosłupa są trójkątami prostokątnymi. | P | F |
| Liczba wszystkich krawędzi ostrosłupa jest parzysta. | P | F |
| Wszystkie ściany boczne ostrosłupa mają wspólny wierzchołek. | P | F |
Wojtek narysował cztery figury (I–IV) składające się z kwadratów i trójkątów równobocznych (zobacz rysunek). Zamierza on dorysować do każdej figury jeden kwadrat albo jeden trójkąt, aby otrzymać z nich siatki graniastosłupa.
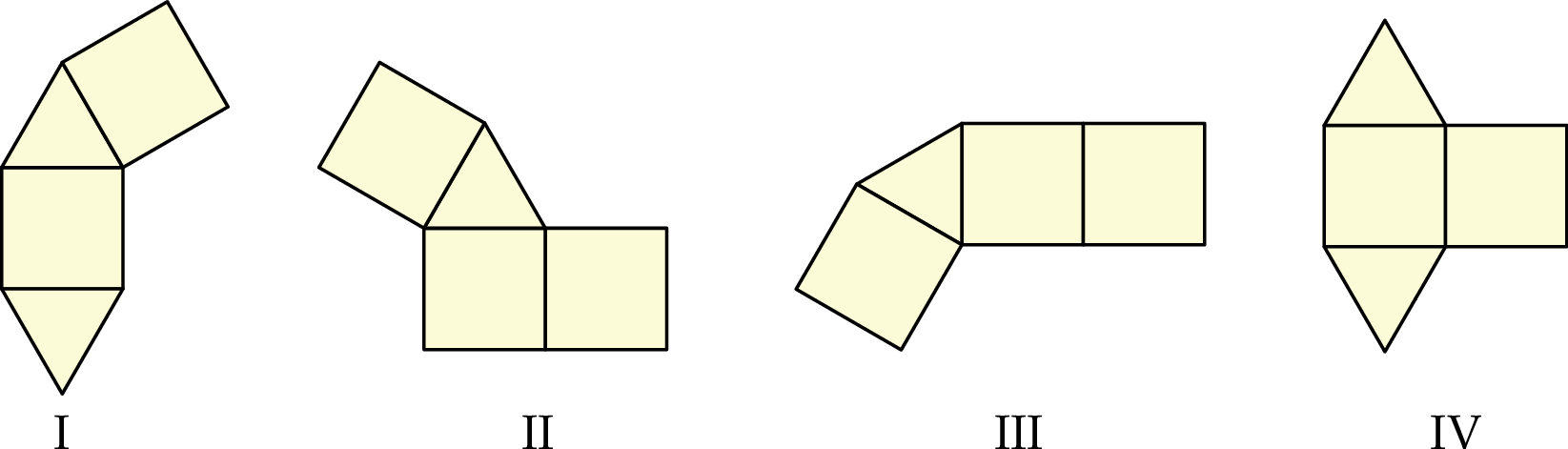
Z której figury nie da się w sposób zaplanowany przez Wojtka otrzymać siatki graniastosłupa?
A) I B) II C) III D) IV
Pole powierzchni całkowitej walca jest równe 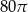 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
A) 3 B) 6 C) 9 D) 18
Pole podstawy stożka jest równe 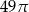 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Tworząca tego stożka ma długość
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Tworząca tego stożka ma długość
A) 7 B) 10,5 C) 21 D) 14
Dane są: kula o promieniu  , walec o promieniu podstawy
, walec o promieniu podstawy  i wysokości
i wysokości  , oraz stożek o promieniu podstawy
, oraz stożek o promieniu podstawy  i tworzącej długości
i tworzącej długości 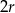 .
.
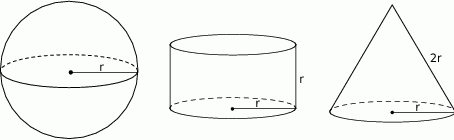
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole powierzchni całkowitej stożka jest równe polu powierzchni kuli. | P | F |
| Pole powierzchni całkowitej walca jest równe polu powierzchni kuli. | P | F |
Metalową kulę o objętości 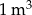 przetopiono na kulki o objętości
przetopiono na kulki o objętości 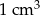 , a następnie otrzymane kulki ustawiono obok siebie w jednej linii tak jak na rysunku.
, a następnie otrzymane kulki ustawiono obok siebie w jednej linii tak jak na rysunku.
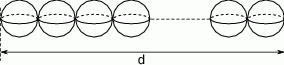
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W wyniku opisanego przetopienia otrzymano 1 000 000 małych kulek. | P | F |
Długość 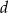 otrzymanej linii kulek jest równa 20 km. otrzymanej linii kulek jest równa 20 km. | P | F |
Promień kuli jest równy 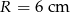 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość tej kuli jest równa 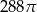 . . | P | F |
Pole powierzchni tej kuli jest równe 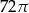 . . | P | F |
Witek ma trzy jednakowe prostopadłościenne klocki. W każdym z tych klocków dwie ściany są kwadratami, a cztery pozostałe – prostokątami. Z tych klocków zbudował figurę przedstawioną na rysunku.
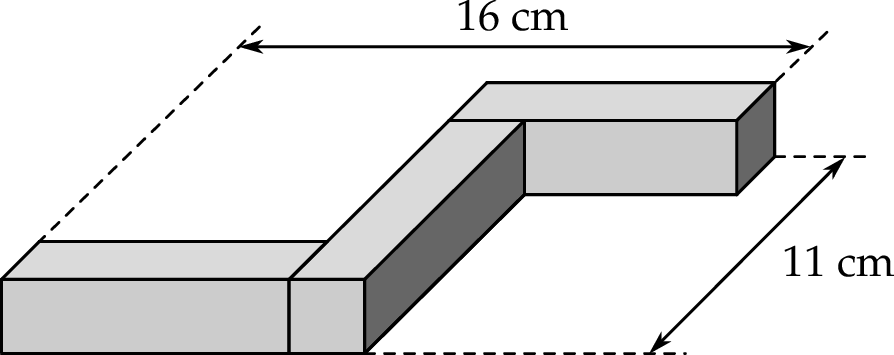
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dłuższe krawędzie prostopadłościennego klocka mają po 8 cm. | P | F |
Objętość jednego klocka jest równa 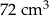 . . | P | F |
Na rysunku przedstawiono siatkę graniastosłupa prostego oraz podano długości niektórych jego krawędzi.
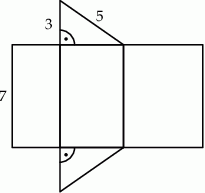
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole największej ściany bocznej tego graniastosłupa jest równe 35. | P | F |
| Pole podstawy tego graniastosłupa jest równe 12. | P | F |
Na rysunku przedstawiono siatkę graniastosłupa prostego oraz podano długości niektórych jego krawędzi.
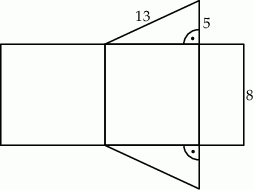
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole największej ściany bocznej tego graniastosłupa jest równe 96. | P | F |
| Pole podstawy tego graniastosłupa jest równe 30. | P | F |
W pudełku są klocki w kształcie ostrosłupów trójkątnych i sześcianów. Klocków w kształcie ostrosłupów trójkątnych jest trzy razy więcej niż klocków sześciennych. Wszystkie klocki mają łącznie 720 krawędzi. Ile klocków w kształcie sześcianu jest w tym pudełku?
A) 24 B) 30 C) 39 D) 40
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
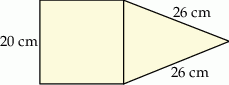
Suma długości krawędzi bocznych tego ostrosłupa jest równa A/B.
A) 360 cm B) 104 cm
Pole powierzchni całkowitej tego ostrosłupa jest równa C/D.
C) 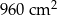 D)
D) 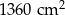
Na rysunku przedstawiono siatkę walca.
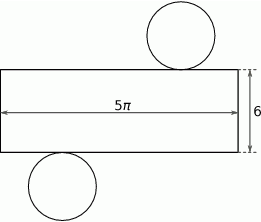
Pole powierzchni całkowitej tego walca jest równe
A) 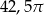 B)
B) 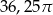 C)
C) 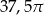 D)
D) 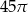
W koszu były 203 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono. Ile klocków odłożono?
A) 150 B) 125 C) 78 D) 53
W koszu były 303 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono. Ile klocków odłożono?
A) 87 B) 125 C) 178 D) 216
Drewniany sześcian rozcięto na identyczne mniejsze sześciany, a następnie usunięto część z nich tworząc trzy puste tunele łączące przeciwległe ściany (zobacz rysunek). Otrzymana w ten sposób bryła została w całości zanurzona w niebieskiej farbie.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Otrzymana bryła składa się ze 110 małych sześcianów. | P | F |
| 24 małe sześciany mają dokładnie jedną ścianę pomalowaną na niebiesko. | P | F |
Dwa sześciany – jeden o krawędzi 2 i drugi o krawędzi 3 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 35 B) 47 C) 94 D) 142
Dwa sześciany – jeden o krawędzi 3 i drugi o krawędzi 4 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 150 B) 222 C) 366 D) 111
Który z poniższych rysunków nie może być siatką ostrosłupa prawidłowego czworokątnego?
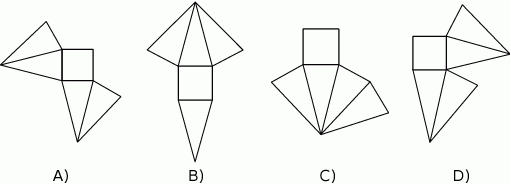
Siatka narysowanego graniastosłupa prostego składa się
A) z 2 trójkątów i 2 prostokątów B) z 2 trójkątów i 3 prostokątów
C) z 3 trójkątów i 2 prostokątów D) z 3 trójkątów i 3 prostokątów
Z jednakowych czworościennych klocków ułożono bryłę mającą kształt czworościanu foremnego.
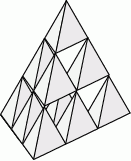
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Utworzona bryła składa się z 10 klocków. | P | F |
| Czworościan foremny o wymiarach takich jak utworzona figura ma objętość 27 razy większą od objętości jednego klocka. | P | F |
