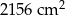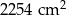Jacek z 14 jednakowych sześciennych kostek skleił figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.
Całą figurę, również od spodu, Jacek pomalował. Ile sześciennych kostek ma pomalowane dokładnie 4 ściany?
A) 8 B) 7 C) 6 D) 5


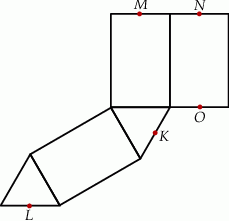
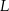 pokryje się z punktem
pokryje się z punktem 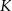
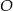
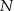
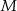
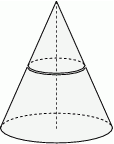
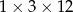
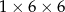
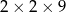
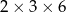
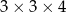
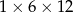
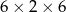
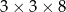
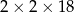
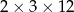
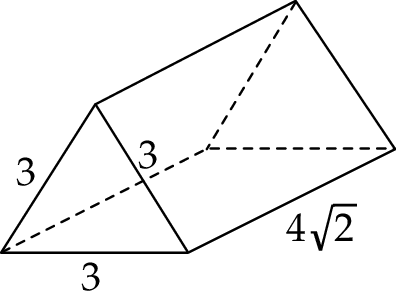
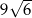
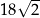
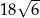
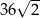
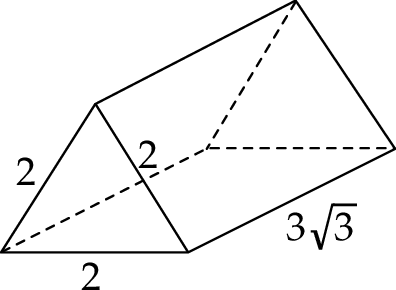

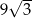
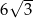
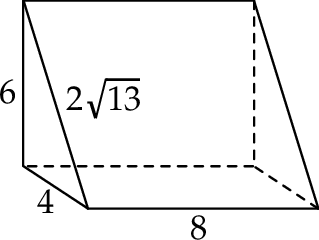
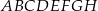 i ostrosłup
i ostrosłup 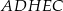 .
. 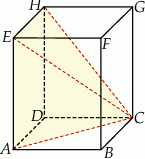
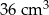 . Objętość ostrosłupa
. Objętość ostrosłupa 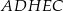 jest równa A/B.
jest równa A/B.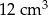
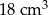
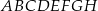 jest równa C/D.
jest równa C/D.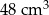
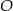 i promieniu
i promieniu  oraz walec o promieniu podstawy
oraz walec o promieniu podstawy  i wysokości
i wysokości  .
. 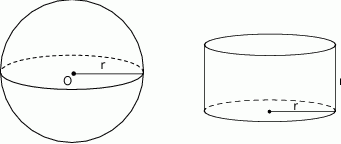
 objętości kuli.
objętości kuli. 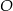 i promieniu
i promieniu  oraz walec o promieniu podstawy
oraz walec o promieniu podstawy  i wysokości
i wysokości 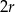 .
. 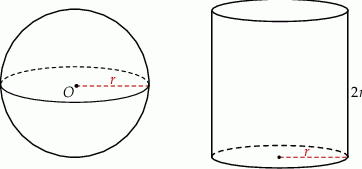
 objętości kuli.
objętości kuli.  objętości kuli.
objętości kuli.  są środkami jego krawędzi.
są środkami jego krawędzi. 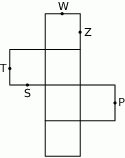
 pokryje się z punktem
pokryje się z punktem
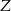
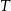
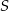
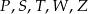 są środkami jego krawędzi.
są środkami jego krawędzi. 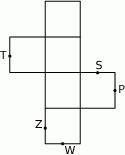
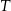 pokryje się z punktem
pokryje się z punktem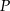
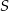
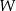
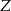
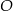 i boku długości 8.
i boku długości 8. 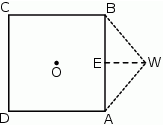
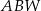 o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C. 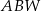 jest równoramienny.
jest równoramienny. 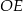 jest mniejsza niż wysokość
jest mniejsza niż wysokość 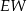 trójkąta
trójkąta 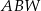 .
. 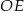 jest większa niż wysokość
jest większa niż wysokość 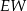 trójkąta
trójkąta 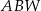 .
.  i boku długości 6.
i boku długości 6. 
 o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.  jest równoramienny.
jest równoramienny. 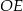 jest mniejsza niż wysokość
jest mniejsza niż wysokość 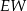 trójkąta
trójkąta 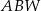 .
. 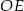 jest większa niż wysokość
jest większa niż wysokość 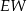 trójkąta
trójkąta 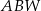 .
. 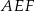 .
. 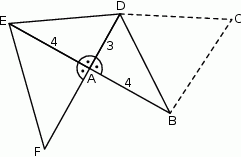
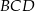 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C. 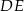 i
i 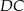 mają różne długości.
mają różne długości. 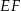 i
i 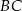 mają różne długości.
mają różne długości. 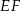 i
i 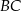 mają równe długości.
mają równe długości. 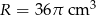 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 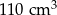 .
. 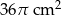 .
.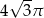
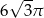
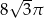
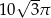
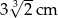 ,
, 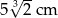 i
i 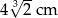 podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa
podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa 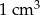
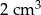
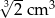
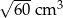
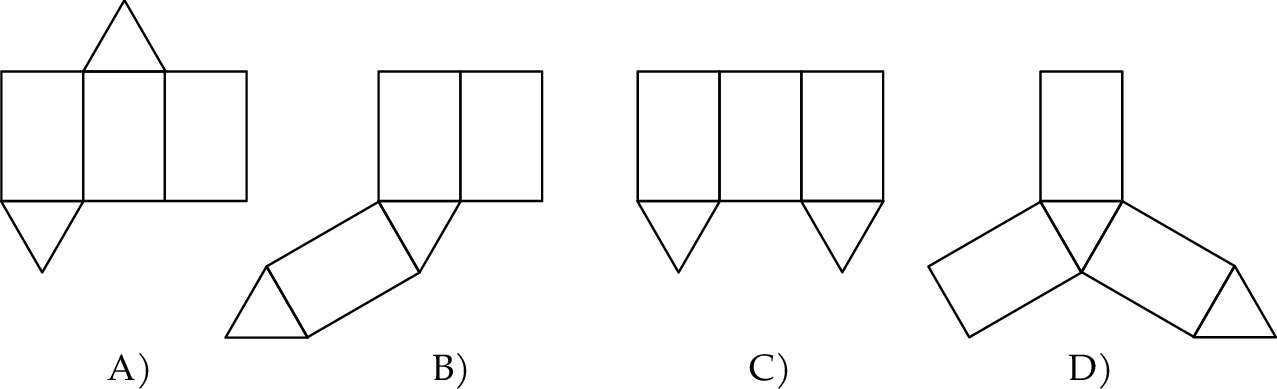
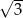 cm zwinięto w stożek.
cm zwinięto w stożek. 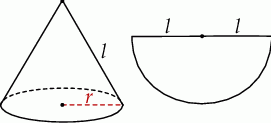
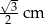
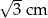
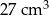 usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe
usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe 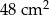
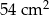
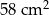
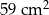
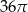 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa 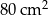 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku. 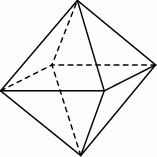
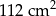
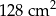
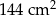
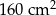
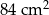 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku. 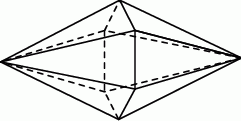
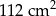

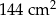
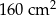
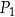 i
i 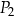 oraz podano długości ich boków.
oraz podano długości ich boków. 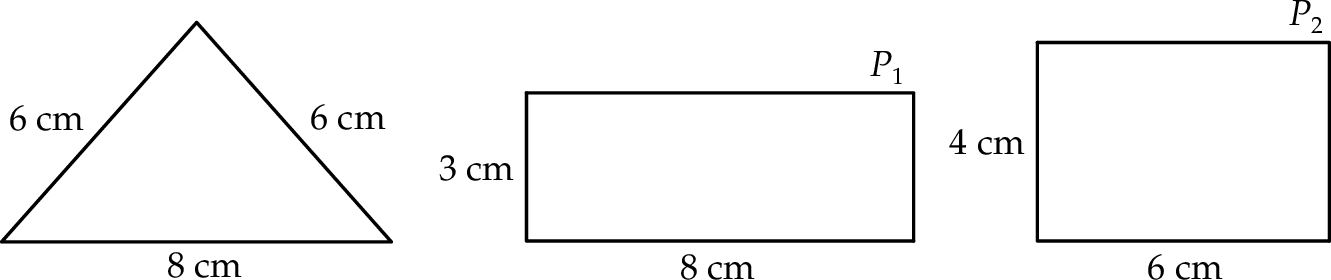
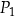 i
i 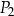 ma bok takiej samej długości jak jeden z boków trójkąta.
ma bok takiej samej długości jak jeden z boków trójkąta. 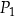 i
i 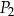 nie mają takich samych wymiarów.
nie mają takich samych wymiarów. 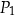 i
i 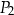 nie mają boku tej samej długości.
nie mają boku tej samej długości. 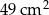 . Z wszystkich tych klocków zbudowano prostopadłościan o objętości
. Z wszystkich tych klocków zbudowano prostopadłościan o objętości 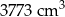 . W koszu znajdowało się A/B klocków.
. W koszu znajdowało się A/B klocków.