Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 4 cm, a wysokość jego ściany bocznej ma długość 5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A)  B)
B)  C)
C)  D)
D) 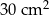
/Szkoła podstawowa/Zadania testowe/Figury przestrzenne
Dany jest ostrosłup prawidłowy czworokątny. Pole powierzchni całkowitej tej bryły jest równe 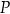 , a jedna ściana boczna ma pole równe
, a jedna ściana boczna ma pole równe 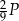 . Pole powierzchni bocznej tego ostrosłupa jest równe A/B.
. Pole powierzchni bocznej tego ostrosłupa jest równe A/B.
A) 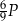 B)
B) 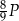
Pole powierzchni podstawy tego ostrosłupa jest dwa razy C/D niż pole powierzchni jego jednej ściany bocznej.
C) mniejsze D) większe
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 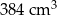 .
.
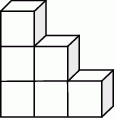
Pole powierzchni całkowitej tej bryły jest równe
A) 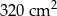 B)
B) 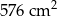 C)
C) 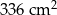 D)
D) 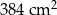
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 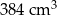 .
.
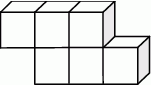
Pole powierzchni całkowitej tej bryły jest równe
A) 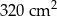 B)
B) 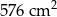 C)
C) 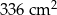 D)
D) 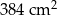
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli średnicę podstawy stożka zwiększymy 3 razy, a jego wysokość zmniejszymy 3 razy, to objętość stożka
A) zwiększy się dziewięciokrotnie. B) zmniejszy się trzykrotnie.
C) zwiększy się trzykrotnie. D) nie zmieni się.
Na rysunku przedstawiono graniastosłup prosty trójkątny oraz jego podstawę. Wysokość tego graniastosłupa jest równa 1 cm.

Pole powierzchni bocznej tego graniastosłupa jest A/B pole jednej podstawy.
A) takie samo jak B) dwa razy większe niż
Pole powierzchni całkowitej tego graniastosłupa jest równe C/D.
C) 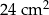 D)
D) 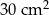
Promień kuli jest równy promieniowi podstawy walca, oraz objętości obu brył są równe. Stosunek pola powierzchni kuli do pola powierzchni całkowitej walca jest równy
A) 1 B)  C)
C) 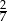 D)
D) 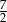
Ewa z sześciennych klocków o krawędzi długości 3 cm skleiła kilka brył o kształcie pokazanym na rysunku.
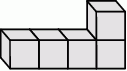
Z czterech takich brył Ewa skleiła graniastosłup prawidłowy czworokątny. Wysokość tego graniastosłupa jest równa A/B.
A) 12 cm B) 15 cm
Pole powierzchni bocznej utworzonego graniastosłupa jest równe C/D.
C) 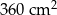 D)
D) 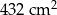
Na siatce sześcianu zaznaczono jego dwie ściany 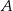 i
i 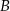 oraz jego dwie krawędzie
oraz jego dwie krawędzie 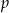 i
i 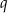 .
.
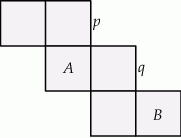
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ściany 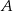 i i 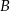 są przeciwległymi ścianami sześcianu. są przeciwległymi ścianami sześcianu. | P | F |
Krawędzie 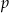 i i 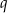 są prostopadłymi krawędziami sześcianu. są prostopadłymi krawędziami sześcianu. | P | F |
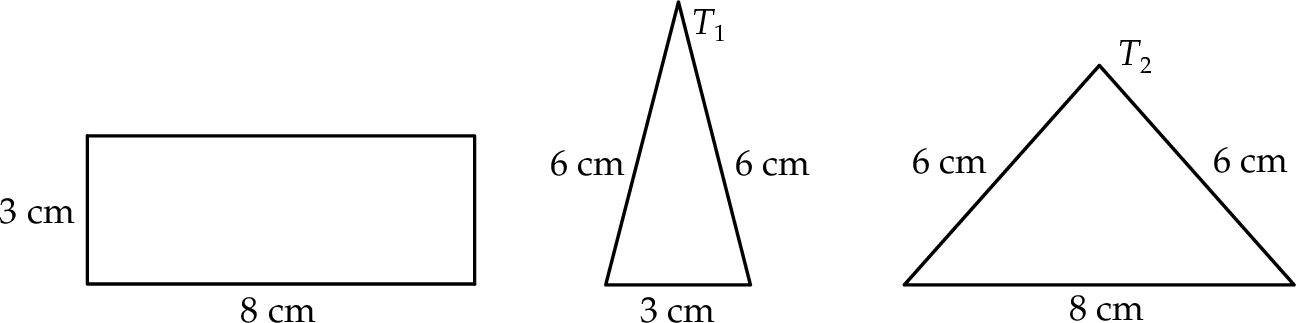
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 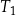 i
i 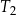 oraz podano długości ich boków.
oraz podano długości ich boków.
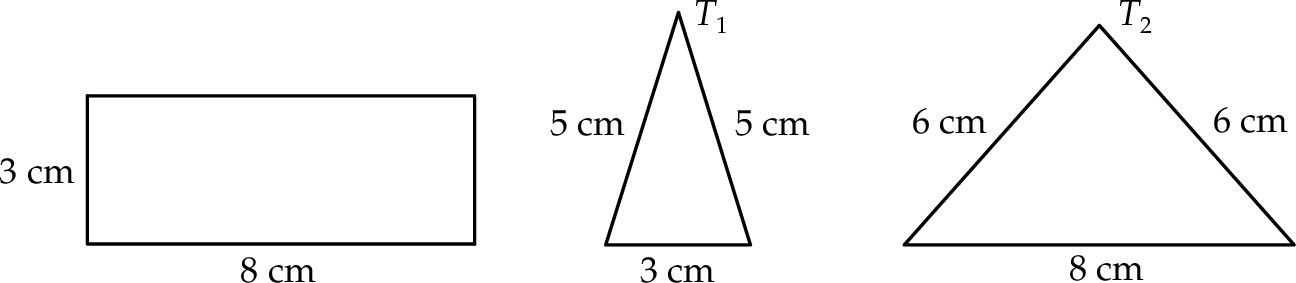
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów 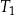 i i 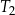 . . |
| B) | trójkąty 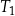 i i 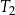 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkąta 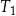 mają inną długość niż ramiona trójkąta mają inną długość niż ramiona trójkąta 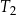 . . |
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 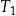 i
i 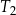 oraz podano długości ich boków.
oraz podano długości ich boków.
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów  i i  . . |
| B) | trójkąty  i i 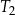 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkątów 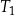 i i 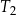 nie są równe długościom boków prostokąta. nie są równe długościom boków prostokąta. |
Siatka ostrosłupa składa się z kwadratu i czterech trójkątów prostokątnych zbudowanych na bokach tego kwadratu.
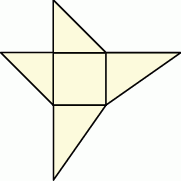
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wysokość tego ostrosłupa jest równa długości jednej z jego krawędzi. | P | F |
| Wszystkie wysokości ścian bocznych tego ostrosłupa mają taką samą długość. | P | F |
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
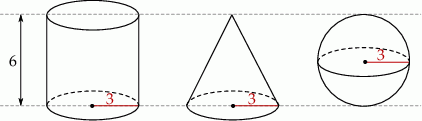
Na podstawie informacji przedstawionych na rysunku wybierz zdanie prawdziwe.
A) Objętość kuli jest większa od objętości walca.
B) Objętość stożka jest większa od objętości kuli.
C) Objętość walca jest 2 razy większa od objętości kuli.
D) Objętość stożka jest 3 razy mniejsza od objętości walca.
Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.
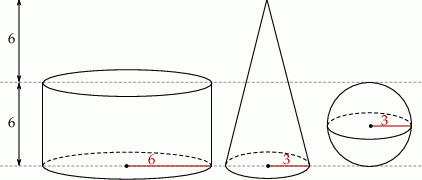
Na podstawie informacji przedstawionych na rysunku wybierz zdanie fałszywe.
A) Objętość kuli jest równa objętości stożka.
B) Objętość walca jest 3 razy większa od objętości stożka.
C) Objętość walca jest 6 razy większa od objętości kuli.
D) Suma objętości stożka i kuli jest mniejsza od objętości walca.
Na rysunku podano wymiary trzech pojemników w kształcie walca.
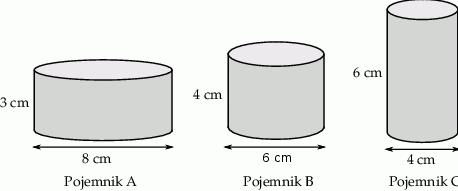
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość pojemnika  stanowi 70% objętości pojemnika stanowi 70% objętości pojemnika 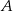 . . | P | F |
Objętość pojemnika 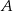 jest dwa razy większa od objętości pojemnika jest dwa razy większa od objętości pojemnika 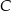 . . | P | F |
Liczba ścian ostrosłupa prawidłowego jest o 5 mniejsza niż liczba jego krawędzi. Pole powierzchni całkowitej tego ostrosłupa jest równe 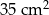 , a pole podstawy jest równe
, a pole podstawy jest równe 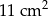 . Pole jednej ściany bocznej tego ostrosłupa jest równe
. Pole jednej ściany bocznej tego ostrosłupa jest równe
A) 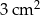 B)
B) 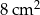 C)
C) 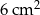 D)
D) 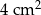
Rozcinając powierzchnię boczną walca o promieniu  otrzymujemy kwadrat. Objętość tego walca wyraża się wzorem
otrzymujemy kwadrat. Objętość tego walca wyraża się wzorem
A) 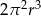 B)
B) 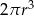 C)
C) 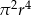 D)
D) 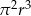
Metalową kulę armatnią o promieniu  przetopiono na metalowy walec o promieniu podstawy równym promieniowi kuli. Wysokość walca jest równa
przetopiono na metalowy walec o promieniu podstawy równym promieniowi kuli. Wysokość walca jest równa
A) 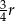 B)
B) 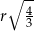 C)
C) 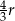 D)
D) 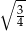
Metalowy walec o promieniu podstawy  i wysokości
i wysokości 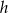 przetopiono na stożek o takim samym promieniu podstawy. Wysokość stożka jest równa
przetopiono na stożek o takim samym promieniu podstawy. Wysokość stożka jest równa
A) 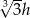 B)
B) 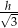 C)
C)  D)
D) 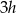
Metalową kulę armatnią o promieniu  przetopiono na metalowy stożek o promieniu podstawy równym promieniowi kuli. Wysokość stożka jest równa
przetopiono na metalowy stożek o promieniu podstawy równym promieniowi kuli. Wysokość stożka jest równa
A) 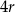 B)
B) 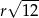 C)
C) 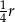 D)
D) 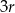
Oskar wykonał model prostopadłościanu. Układał i sklejał ze sobą kolejno drewniane klocki sześcienne o krawędzi 4 cm wzdłuż każdej ściany prostopadłościennego pudełka o wymiarach: 36 cm, 28 cm, 20 cm. Na rysunku przedstawiono część wykonanego modelu (model jest w środku pusty).
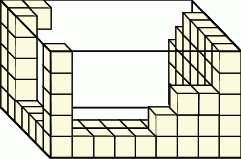
Ile klocków łącznie zużył Oskar na wykonanie całego modelu?
A) 315 B) 230 C) 246 D) 210
Pewien ostrosłup ma o 113 więcej krawędzi, niż wierzchołków. Graniastosłup o takiej samej podstawie, jaką ma ten ostrosłup, ma A/B ścian.
A) 114 B) 116
Wielokąt w podstawie ostrosłupa ma o C/D więcej krawędzi, niż jego jedna ściana boczna.
C) 111 D) 112
Bryłę ułożono z jednakowych sześciennych klocków. Na rysunkach przedstawiony jest widok tej bryły z dwóch stron.
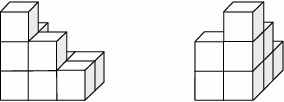
Z ilu klocków składa się ta bryła?
A) 7 B) 8 C) 9 D) 10
Każdy z dwóch jednakowych sześcianów o krawędzi 2 cm podzielono na mniejsze sześciany o krawędzi 1 cm. Czy z otrzymanych w ten sposób małych sześciennych kostek można ułożyć jeden pełny sześcian, tak by wszystkie kostki były wykorzystane? Wybierz odpowiedź T lub N i jej uzasadnienie wybrane spośród A, B, C, D.
| Tak | Nie |
| ponieważ | |
| A) | Liczba małych kostek nie jest podzielna przez 3. |
| B) | Liczba małych kostek jest potęgą liczby 2. |
| C) | Liczba małych kostek jest drugą potęgą liczby naturalnej. |
| D) | Liczba małych kostek nie jest trzecią potęgą liczby naturalnej. |
Kula o promieniu 5 cm i stożek o promieniu podstawy 10 cm mają równe objętości. Wysokość stożka jest równa
A) 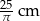 B) 10 cm C)
B) 10 cm C) 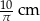 D) 5 cm
D) 5 cm
Promień kuli i promień podstawy stożka są równe 4. Pole powierzchni kuli jest równe polu powierzchni całkowitej stożka. Długość tworzącej stożka jest równa
A) 8 B) 4 C) 16 D) 12
Pole powierzchni kuli o promieniu 6 cm jest równe polu powierzchni całkowitej stożka o promieniu podstawy 8 cm. Pole powierzchni bocznej stożka jest równe
A) 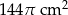 B)
B) 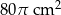 C)
C) 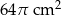 D)
D) 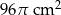
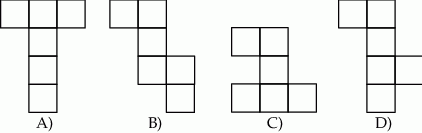
Który z poniższych rysunków nie może być siatką sześcianu?
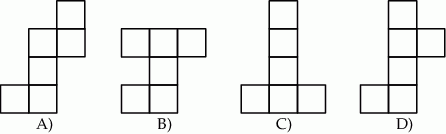
Który z poniższych rysunków nie może być siatką sześcianu?