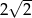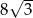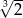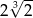Siatka ostrosłupa składa się z kwadratu i trójkątów równobocznych zbudowanych na bokach tego kwadratu.
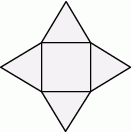
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wszystkie krawędzie tego ostrosłupa mają taką samą długość. | P | F |
| Wysokość tego ostrosłupa jest mniejsza niż wysokość jego ściany bocznej. | P | F |

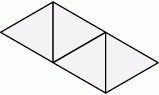
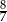
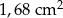
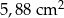
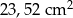
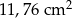
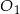 i
i 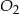 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 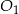 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 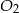 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 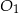 do objętości ostrosłupa
do objętości ostrosłupa 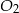 jest równy
jest równy 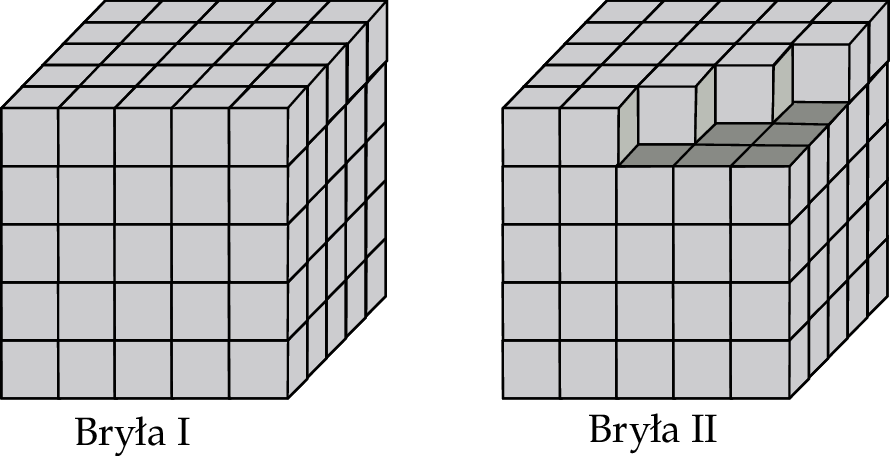
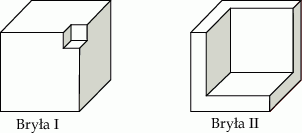
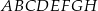 oraz trzy jego przekątne.
oraz trzy jego przekątne. 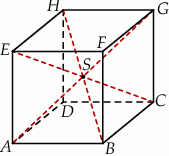
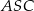 i
i 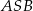 są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C. 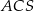 i
i 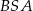 nie są przystające.
nie są przystające. 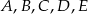 są środkami jej krawędzi.
są środkami jej krawędzi. 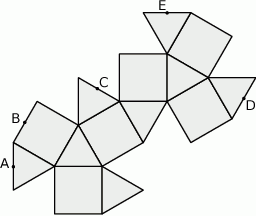
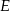 pokryje się z punktem
pokryje się z punktem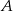
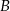
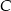
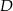
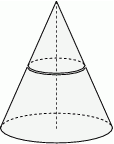
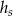 i walec o wysokości
i walec o wysokości 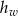 mają takie same podstawy o polu
mają takie same podstawy o polu 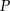 . Stożek ma dwa razy większą objętość niż walec, czyli
. Stożek ma dwa razy większą objętość niż walec, czyli 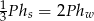 .
.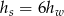
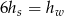
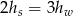
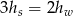
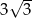
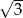
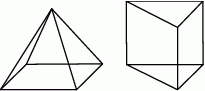
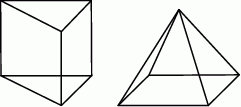
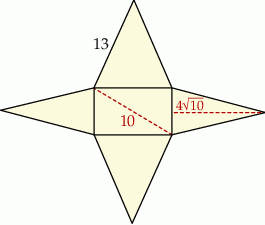
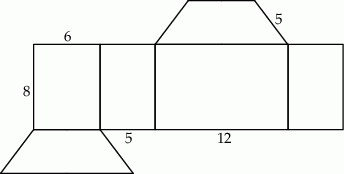
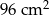 kartonu, a na graniastosłup o
kartonu, a na graniastosłup o 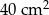 więcej (nie wliczając powierzchni zakładek).
więcej (nie wliczając powierzchni zakładek).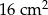 kartonu.
kartonu.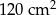 .
.