Funkcja 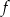 jest określona wzorem
jest określona wzorem 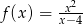 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 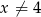 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 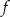 w punkcie
w punkcie 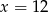 .
.
/Szkoła średnia/Funkcje
Funkcja 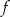 jest określona wzorem
jest określona wzorem 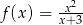 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 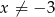 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 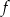 w punkcie
w punkcie 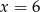 .
.
Dana jest funkcja 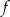 określona wzorem
określona wzorem 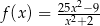 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz wartość
. Oblicz wartość 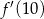 pochodnej tej funkcji dla argumentu 10.
pochodnej tej funkcji dla argumentu 10.
Dana jest funkcja 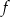 określona wzorem
określona wzorem 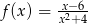 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej  . Oblicz wartość pochodnej tej funkcji w punkcie
. Oblicz wartość pochodnej tej funkcji w punkcie 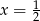 .
.
Oblicz pochodną funkcji 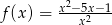 w punkcie
w punkcie 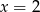 .
.
Dana jest funkcja 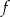 określona wzorem
określona wzorem 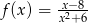 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej  . Oblicz wartość pochodnej tej funkcji w punkcie
. Oblicz wartość pochodnej tej funkcji w punkcie 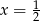 .
.
Dana jest funkcja 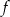 określona wzorem
określona wzorem 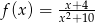 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej  . Oblicz wartość pochodnej tej funkcji w punkcie
. Oblicz wartość pochodnej tej funkcji w punkcie 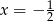 .
.
Funkcja 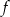 jest określona wzorem
jest określona wzorem 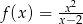 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 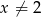 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 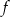 w punkcie
w punkcie 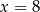 .
.
Dana jest funkcja 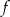 określona wzorem
określona wzorem 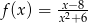 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej  . Oblicz wartość pochodnej tej funkcji w punkcie
. Oblicz wartość pochodnej tej funkcji w punkcie 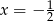 .
.
Funkcja 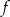 jest określona wzorem
jest określona wzorem 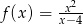 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 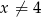 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 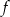 w punkcie
w punkcie 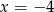 .
.
Funkcja 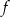 jest określona wzorem
jest określona wzorem 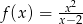 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 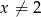 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 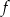 w punkcie
w punkcie 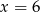 .
.
Dana jest funkcja 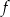 określona wzorem
określona wzorem 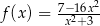 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz wartość
. Oblicz wartość 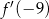 pochodnej tej funkcji dla argumentu
pochodnej tej funkcji dla argumentu 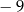 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 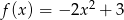 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 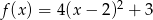 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 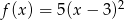 .
.
Oblicz granicę jednostronną funkcji 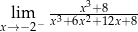 .
.
Udowodnij, że jeżeli 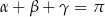 , to
, to
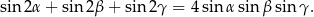
Wielomiany 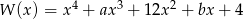 oraz
oraz 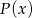 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zad/3139795/HzadT2x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości  i
i 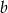 .
.
Wielomiany 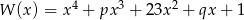 oraz
oraz 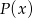 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zad/1984880/HzadT2x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości 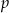 i
i 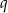 .
.
Napisz wzór i narysuj wykres funkcji 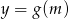 , która każdej liczbie rzeczywistej
, która każdej liczbie rzeczywistej 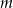 przyporządkowuje najmniejszą wartość funkcji kwadratowej
przyporządkowuje najmniejszą wartość funkcji kwadratowej 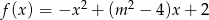 w przedziale
w przedziale 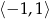 .
.
Oblicz granicę jednostronną 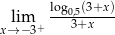 .
.
Funkcja 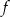 ma następujące własności:
ma następujące własności:
1. Dziedziną funkcji jest przedział 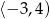 .
.
2. Przedział 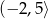 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji 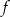 .
.
3. Funkcja ma dwa miejsca zerowe -2 oraz 3.
4. Funkcja 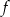 jest rosnąca w przedziale
jest rosnąca w przedziale 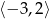 i malejąca w przedziale
i malejąca w przedziale 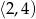 . Podaj zbiór rozwiązań nierówności
. Podaj zbiór rozwiązań nierówności 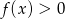 .
.
Znajdź taką wartość parametru 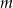 , aby największa wartość funkcji
, aby największa wartość funkcji 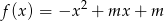 była najmniejsza z możliwych.
była najmniejsza z możliwych.
Wykaż, że wszystkie wartości funkcji 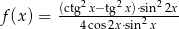 są większe od 1.
są większe od 1.
Wielomian 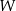 jest wielomianem stopnia 5 i spełnia warunki:
jest wielomianem stopnia 5 i spełnia warunki: 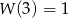 oraz
oraz 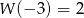 . Wykaż, że nie wszystkie współczynniki wielomianu
. Wykaż, że nie wszystkie współczynniki wielomianu 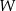 są liczbami całkowitymi.
są liczbami całkowitymi.
Wyznacz dziedzinę funkcji 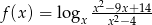 .
.
Wyznacz dziedzinę funkcji określonej wzorem 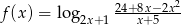 .
.
Wyznacz największą wartość funkcji 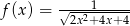 .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 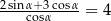 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 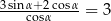 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 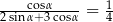 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Dany jest trójmian kwadratowy 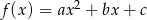 .
.
- Dla
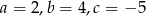 wyznacz największą i najmniejszą wartość tego trójmianu w przedziale
wyznacz największą i najmniejszą wartość tego trójmianu w przedziale 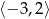 .
. - Wyznacz wzór trójmianu w postaci iloczynowej, jeśli wiadomo, że ma on miejsca zerowe
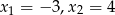 , a do jego wykresu należy punkt
, a do jego wykresu należy punkt 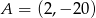 .
.
Funkcja 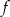 jest określona wzorem
jest określona wzorem 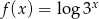 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 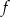 w punkcie
w punkcie 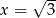
Funkcja 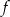 jest określona wzorem
jest określona wzorem 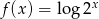 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 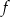 w punkcie
w punkcie 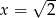
Właściciel pewnej piekarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 28 kolejnych dni. Przyjmijmy, że liczbę 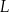 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
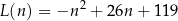
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 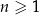 i
i 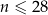 . W którym dniu analizowanego okresu w piekarni obsłużono największą, a w którym dniu najmniejszą liczbę klientów? Oblicz liczby klientów obsłużonych w tych dniach.
. W którym dniu analizowanego okresu w piekarni obsłużono największą, a w którym dniu najmniejszą liczbę klientów? Oblicz liczby klientów obsłużonych w tych dniach.
Reszta z dzielenia wielomianu 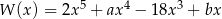 przez trójmian
przez trójmian 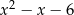 jest równa
jest równa 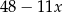 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 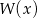 przez trójmian
przez trójmian 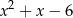 .
.
Oblicz granicę 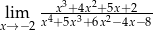 .
.
Oblicz granicę
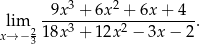
Zapisz wzór funkcji 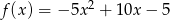 w postaci kanonicznej i iloczynowej.
w postaci kanonicznej i iloczynowej.

