Oblicz wartość wyrażenia 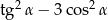 , jeżeli
, jeżeli 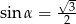 i
i  jest kątem ostrym.
jest kątem ostrym.
/Szkoła średnia/Funkcje
Kąt  jest ostry i
jest ostry i  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 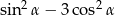 .
.
Kąt  jest ostry i
jest ostry i 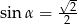 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 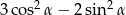 .
.
Wyznacz wszystkie wartości parametrów 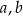 i
i  , dla których wielomian
, dla których wielomian
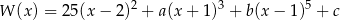
jest podzielny przez wielomian 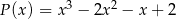 .
.
Oblicz granicę 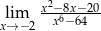 .
.
Oblicz granicę 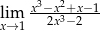 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 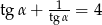 oblicz
oblicz 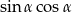 .
.
Kąt  jest ostry i
jest ostry i 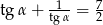 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 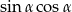 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 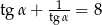 oblicz
oblicz 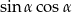 .
.
Funkcja kwadratowa 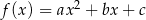 ma dwa miejsca zerowe
ma dwa miejsca zerowe 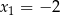 i
i 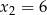 . Wykres funkcji
. Wykres funkcji 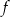 przechodzi przez punkt
przechodzi przez punkt 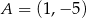 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 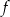 .
.
Funkcja kwadratowa 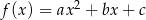 ma dwa miejsca zerowe
ma dwa miejsca zerowe 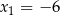 i
i 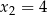 . Wykres funkcji
. Wykres funkcji 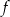 przechodzi przez punkt
przechodzi przez punkt 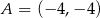 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 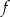 .
.
Parabola, która jest wykresem funkcji kwadratowej 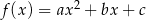 , przechodzi przez punkt
, przechodzi przez punkt 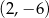 oraz
oraz 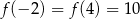 . Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
. Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
Udowodnij, że jeżeli 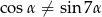 i
i 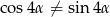 to
to
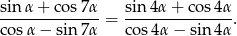
Wykresem funkcji kwadratowej 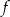 określonej wzorem
określonej wzorem 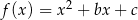 jest parabola, na której leży punkt
jest parabola, na której leży punkt 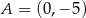 . Osią symetrii tej paraboli jest prosta o równaniu
. Osią symetrii tej paraboli jest prosta o równaniu 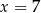 . Oblicz wartości współczynników
. Oblicz wartości współczynników 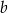 i
i  .
.
Osią symetrii wykresu funkcji kwadratowej 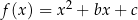 jest prosta o równaniu
jest prosta o równaniu 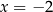 . Jednym z miejsc zerowych funkcji
. Jednym z miejsc zerowych funkcji 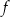 jest liczba 1. Oblicz współczynniki
jest liczba 1. Oblicz współczynniki 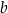 oraz
oraz  .
.
Wykresem funkcji kwadratowej 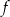 określonej wzorem
określonej wzorem 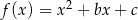 jest parabola, na której leży punkt
jest parabola, na której leży punkt 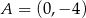 . Osią symetrii tej paraboli jest prosta o równaniu
. Osią symetrii tej paraboli jest prosta o równaniu 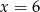 . Oblicz wartości współczynników
. Oblicz wartości współczynników 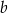 i
i  .
.
Wielomian 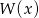 stopnia 3 jest podzielny przez trójmian kwadratowy
stopnia 3 jest podzielny przez trójmian kwadratowy 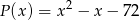 . Wiadomo ponadto, że
. Wiadomo ponadto, że 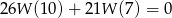 . Wyznacz miejsca zerowe wielomianu
. Wyznacz miejsca zerowe wielomianu 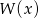 .
.
Funkcja 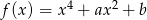 przyjmuje wartość 1 dla czterech argumentów:
przyjmuje wartość 1 dla czterech argumentów:
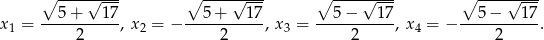
Oblicz najmniejszą wartość tej funkcji.
Uzasadnij, że liczba 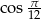 jest niewymierna.
jest niewymierna.
Udowodnij, że jeżeli 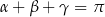 , to
, to
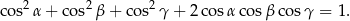
Funkcja 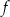 jest określona wzorem
jest określona wzorem 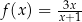 dla każdego
dla każdego 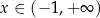 . Wykaż, że
. Wykaż, że 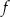 jest funkcją rosnącą.
jest funkcją rosnącą.
Reszta z dzielenia wielomianu 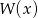 przez trójmian kwadratowy
przez trójmian kwadratowy 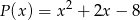 jest równa
jest równa 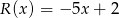 . Wyznacz resztę z dzielenia tego wielomianu przez dwumian
. Wyznacz resztę z dzielenia tego wielomianu przez dwumian 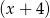 .
.
Dana jest rodzina funkcji kwadratowych zmiennej rzeczywistej  , opisana wzorem
, opisana wzorem 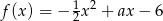 , gdzie
, gdzie  jest liczbą rzeczywistą.
jest liczbą rzeczywistą.
- Dla
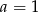 wyznacz zbiór tych argumentów, dla których funkcja
wyznacz zbiór tych argumentów, dla których funkcja 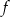 przyjmuje wartości większe niż funkcja liniowa
przyjmuje wartości większe niż funkcja liniowa 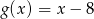 .
. - Wyznacz liczbę
 , dla której zbiorem wartości funkcji
, dla której zbiorem wartości funkcji 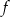 jest przedział
jest przedział 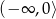 .
. - Dla
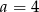 napisz wzór funkcji
napisz wzór funkcji 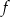 w postaci kanonicznej i narysuj jej wykres.
w postaci kanonicznej i narysuj jej wykres.
Oblicz granicę jednostronną funkcji 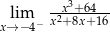 .
.
Oblicz granicę jednostronną funkcji 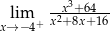 .
.
Oblicz granicę 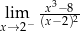 .
.
Dla jakich wartości parametru 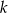 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 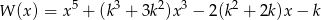 przez dwumian
przez dwumian 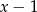 jest nie większa od (–2)?
jest nie większa od (–2)?
Dana jest funkcja 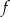 określona wzorem
określona wzorem 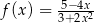 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  , oraz dwie liczby:
, oraz dwie liczby: 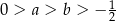 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
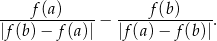
Wyznaczyć dziedzinę funkcji 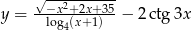 .
.
Porównaj liczby: 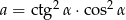 i
i 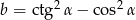 , jeżeli
, jeżeli 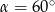 .
.
Funkcja 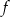 określona jest wzorem
określona jest wzorem 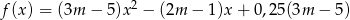 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 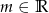 , dla których najmniejsza wartość funkcji
, dla których najmniejsza wartość funkcji 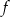 jest liczbą dodatnią.
jest liczbą dodatnią.

