Wielomian 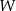 dany jest wzorem
dany jest wzorem 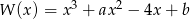 .
.
- Wyznacz
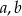 oraz
oraz  tak, aby wielomian
tak, aby wielomian 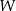 był równy wielomianowi
był równy wielomianowi 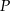 , gdy
, gdy 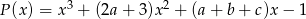 .
. - Dla
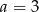 i
i 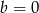 zapisz wielomian
zapisz wielomian 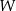 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wielomian 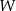 dany jest wzorem
dany jest wzorem 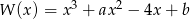 .
.
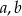 oraz
oraz  tak, aby wielomian
tak, aby wielomian 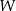 był równy wielomianowi
był równy wielomianowi 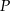 , gdy
, gdy 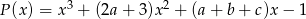 .
. 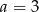 i
i 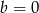 zapisz wielomian
zapisz wielomian 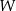 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.Posługując się wzorem 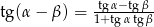 oblicz
oblicz 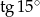 .
.
Wyznacz zbiór wartości funkcji 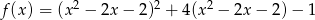 .
.
Dany jest wielomian 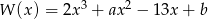 . Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu
. Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu 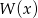 przez
przez 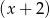 jest równa 20. Oblicz współczynniki
jest równa 20. Oblicz współczynniki  i
i 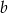 oraz pozostałe pierwiastki wielomianu
oraz pozostałe pierwiastki wielomianu 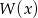 .
.
Reszta z dzielenia wielomianu 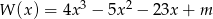 przez dwumian
przez dwumian 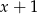 jest równa 20. Oblicz wartość współczynnika
jest równa 20. Oblicz wartość współczynnika 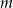 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Reszta z dzielenia wielomianu 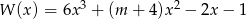 przez dwumian
przez dwumian 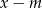 jest równa 8. Oblicz wartość
jest równa 8. Oblicz wartość 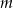 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Maksymalny przedział, na którym funkcja 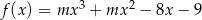 jest malejąca ma długość 2. Oblicz wartość parametru
jest malejąca ma długość 2. Oblicz wartość parametru 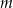 oraz wyznacz największą wartość funkcji na przedziale
oraz wyznacz największą wartość funkcji na przedziale 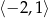 .
.
Sprawdź tożsamość: 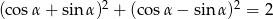 .
.
Uzasadnij, że równość 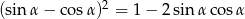 jest tożsamością trygonometryczną.
jest tożsamością trygonometryczną.
Uzasadnij, że równość 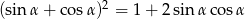 jest tożsamością trygonometryczną.
jest tożsamością trygonometryczną.
Do wykresu pewnej funkcji kwadratowej 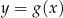 należy punkt o współrzędnych
należy punkt o współrzędnych 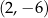 . Osią symetrii wykresu tej funkcji jest prosta o równaniu
. Osią symetrii wykresu tej funkcji jest prosta o równaniu 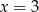 , a jednym z miejsc zerowych funkcji
, a jednym z miejsc zerowych funkcji 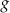 jest
jest 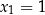 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 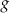 w postaci iloczynowej.
w postaci iloczynowej.
Wyznacz najmniejszą i największą wartość funkcji 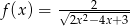 na przedziale
na przedziale 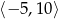 .
.
Wyznacz najmniejszą i największą wartość funkcji 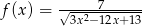 na przedziale
na przedziale 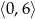 .
.
Kąt  jest ostry i
jest ostry i 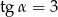 . Oblicz
. Oblicz 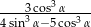 .
.
Funkcja kwadratowa 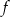 przyjmuje największą wartość równą
przyjmuje największą wartość równą 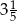 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 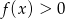 jest przedział
jest przedział 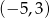 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 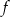 w postaci ogólnej.
w postaci ogólnej.
Wyznacz zbiór wartości funkcji: 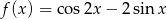 , gdzie
, gdzie 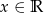 .
.
Wyznacz zbiór wartości funkcji: 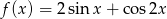 , gdzie
, gdzie 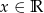 .
.
Oblicz najmniejszą wartość wielomianu 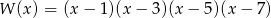 .
.
Reszty z dzielenia wielomianu 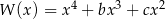 przez dwumiany
przez dwumiany 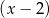 i
i 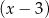 są odpowiednio równe
są odpowiednio równe 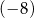 oraz
oraz 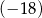 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 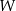 przez dwumian
przez dwumian 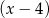 .
.
Kąt  jest ostry oraz
jest ostry oraz 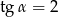 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 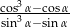 .
.
Kąt  jest ostry oraz
jest ostry oraz 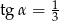 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 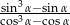 .
.
Dla jakich wartości parametru  , wielomian
, wielomian 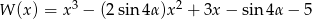 jest podzielny przez dwumian
jest podzielny przez dwumian 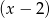 ?
?
Oblicz pochodną funkcji 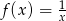 .
.
Wykaż, że
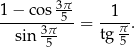
Kąt  jest kątem ostrym. Wiedząc, że
jest kątem ostrym. Wiedząc, że 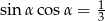 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 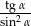 .
.
Kąt  jest ostry i
jest ostry i 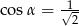 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 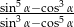 .
.
