Wyznacz te wartości parametru 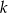 , dla których dziedziną funkcji
, dla których dziedziną funkcji 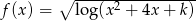 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych.
/Szkoła średnia/Funkcje
Oblicz granicę funkcji 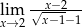 .
.
Oblicz granicę funkcji 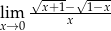 .
.
Oblicz granicę funkcji 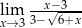 .
.
Oblicz granicę funkcji 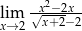 .
.
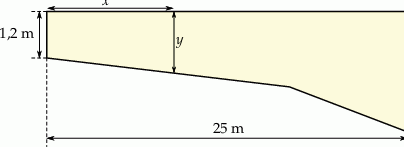
Basen ma długość 25 m. W najpłytszym miejscu jego głębokość jest równa 1,2 m. Przekrój podłużny tego basenu przedstawiono poglądowo na rysunku. Głębokość 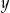 basenu zmienia się wraz z odległością
basenu zmienia się wraz z odległością  od brzegu w sposób opisany funkcją:
od brzegu w sposób opisany funkcją:
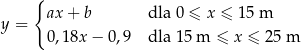
Odległość  jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości
jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości  i
i 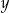 są wyrażone w metrach.
są wyrażone w metrach.
Oblicz wartość współczynnika
 oraz wartość współczynnika
oraz wartość współczynnika 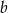 .
. Basen ma długość 25 m. Przy głębszym z brzegów jego głębokość jest równa 1,8 m. Przekrój podłużny tego basenu przedstawiono poglądowo na rysunku. Głębokość 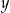 basenu zmienia się wraz z odległością
basenu zmienia się wraz z odległością  od brzegu w sposób opisany funkcją:
od brzegu w sposób opisany funkcją:
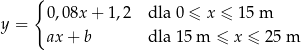
Odległość  jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości
jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości  i
i 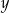 są wyrażone w metrach.
są wyrażone w metrach.
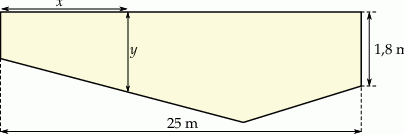
Oblicz wartość współczynnika
 oraz wartość współczynnika
oraz wartość współczynnika 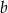 .
. Dach przybudówki przy hali magazynowej ma szerokość 25 metrów. Wysokość tego dachu w najniższym miejscu jest równa 5,4 m. Przekrój poprzeczny przybudówki przedstawiono poglądowo na rysunku. Wysokość dachu 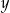 zmienia się wraz z odległością
zmienia się wraz z odległością  od hali magazynowej w sposób opisany funkcją:
od hali magazynowej w sposób opisany funkcją:
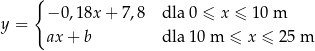
Wielkości  i
i 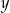 są wyrażone w metrach.
są wyrażone w metrach.
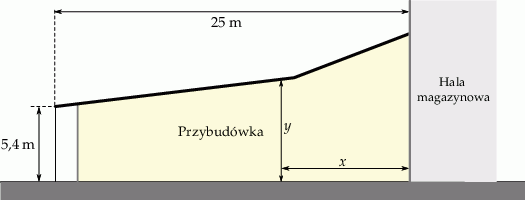
Oblicz wartość współczynnika
 oraz wartość współczynnika
oraz wartość współczynnika 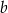 .
. Wyznacz przedziały monotoniczności funkcji 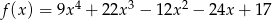 .
.
Zbadaj, czy istnieje taka wartość współczynnika  , dla której wielomiany
, dla której wielomiany 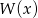 i
i ![[Q (x)]2](https://img.zadania.info/zad/4602131/HzadT2x.gif) są równe, jeśli
są równe, jeśli 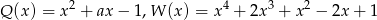 .
.
Funkcja kwadratowa 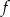 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 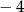 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 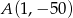 . Napisz wzór funkcji
. Napisz wzór funkcji 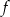 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 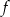 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 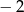 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 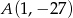 . Napisz wzór funkcji
. Napisz wzór funkcji 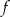 w postaci ogólnej.
w postaci ogólnej.
Wyznacz wszystkie argumenty  , w których funkcja
, w których funkcja 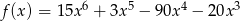 ma ekstrema lokalne.
ma ekstrema lokalne.
Funkcja kwadratowa 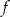 określona jest wzorem
określona jest wzorem 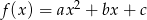 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 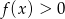 jest przedział
jest przedział 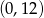 . Największa wartość funkcji
. Największa wartość funkcji 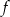 jest równa 9. Oblicz współczynniki
jest równa 9. Oblicz współczynniki  i
i  funkcji
funkcji 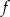 .
.
Funkcja kwadratowa 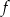 określona jest wzorem
określona jest wzorem 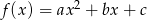 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 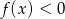 jest przedział
jest przedział 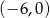 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 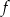 jest równa
jest równa 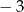 . Oblicz współczynniki
. Oblicz współczynniki 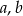 i
i  funkcji
funkcji 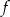 .
.
Dana jest funkcja 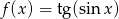 .
.
- Wyznacz dziedzinę i zbiór wartości tej funkcji.
- Czy funkcja jest okresowa?
Znajdź wszystkie funkcje liniowe określone na zbiorze 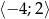 , których zbiorem wartości jest przedział
, których zbiorem wartości jest przedział 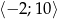 .
.
Wyznacz dziedzinę funkcji 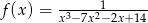 .
.
Wyznacz dziedzinę wyrażenia wymiernego: 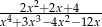 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 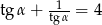 , oblicz
, oblicz 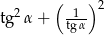 .
.
Wiedząc, że 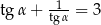 , oblicz
, oblicz 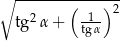 .
.
Zapisz wzór funkcji 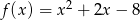 w postaci iloczynowej.
w postaci iloczynowej.
Zapisz wzór funkcji 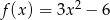 w postaci iloczynowej.
w postaci iloczynowej.
Zapisz wzór funkcji 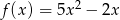 w postaci iloczynowej.
w postaci iloczynowej.
Funkcja kwadratowa 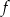 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 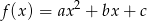 . Największa wartość funkcji
. Największa wartość funkcji 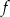 jest równa 6 oraz
jest równa 6 oraz 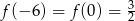 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
Funkcja kwadratowa 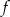 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 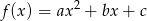 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 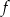 jest równa
jest równa 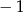 oraz
oraz 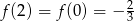 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
Wyznacz największą wartość funkcji 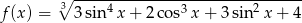 .
.
Wyznacz wartość największą i najmniejszą funkcji 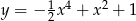 w przedziale
w przedziale 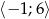 .
.
Oblicz 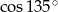 .
.
Oblicz 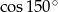 .
.
Wykaż, że jeżeli 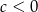 , to trójmian kwadratowy
, to trójmian kwadratowy 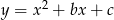 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Dane są dwie funkcje kwadratowe 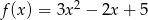 i
i 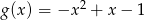 . Wyznacz największą wartość funkcji
. Wyznacz największą wartość funkcji 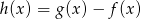 .
.
Rozłóż na czynniki drugiego stopnia wielomian 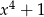 .
.

