Dla jakiej wartości parametru 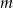 wielomian
wielomian 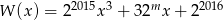 jest podzielny przez dwumian
jest podzielny przez dwumian 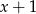 .
.
/Szkoła średnia/Funkcje
Wykaż, że dla dowolnego kąta  takiego, że
takiego, że 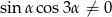 zachodzi tożsamość
zachodzi tożsamość
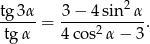
Wielomian 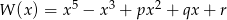 jest podzielny przez wielomian
jest podzielny przez wielomian 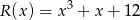 . Wyznacz liczby
. Wyznacz liczby 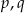 i
i  .
.
Wielomian 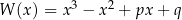 można dwukrotnie podzielić bez reszty przez dwumian
można dwukrotnie podzielić bez reszty przez dwumian 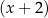 . Oblicz
. Oblicz 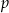 i
i 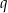 .
.
Reszta z dzielenia wielomianu 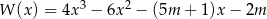 przez dwumian
przez dwumian 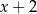 jest równa
jest równa 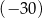 . Oblicz
. Oblicz 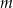 i dla wyznaczonej wartości
i dla wyznaczonej wartości 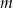 rozwiąż nierówność
rozwiąż nierówność 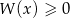 .
.
Wyznacz najmniejszą 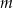 i największą
i największą 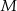 wartość funkcji
wartość funkcji 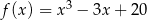 w przedziale
w przedziale 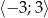 .
.
Zbiorem wartości funkcji kwadratowej 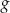 jest przedział
jest przedział 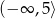 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 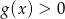 jest przedział
jest przedział 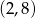 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 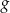 .
.
Dane są wielomiany 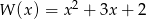 ,
, 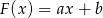 ,
, 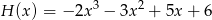 . Wyznacz współczynniki
. Wyznacz współczynniki 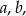 dla których wielomiany
dla których wielomiany 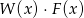 oraz
oraz 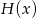 są równe.
są równe.
- Narysuj wykresy funkcji
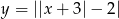 oraz
oraz 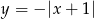 , gdzie
, gdzie 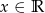 .
. - Wyznacz te wartości parametru
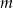 , dla których równanie
, dla których równanie 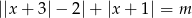 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Funkcja 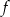 określona jest wzorem
określona jest wzorem 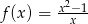 .
.
- Wykaż ze zbiorem wartości funkcji
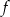 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych. - Uzasadnij, że funkcja
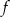 nie jest rożnowartościowa.
nie jest rożnowartościowa.
Wykaż, że 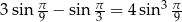 .
.
Dane są wielomiany 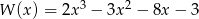 i
i 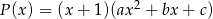 .
.
- Wyznacz współczynniki
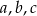 tak, aby
tak, aby 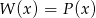 .
. - Przedstaw wielomian
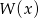 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Dana jest funkcja 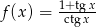 dla
dla 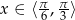 .
.
- Rozwiąż równanie
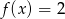 .
. - Wyznacz najmniejszą wartość funkcji
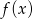 .
.
Wyznacz wszystkie wartości parametru 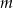 , dla których dziedziną funkcji
, dla których dziedziną funkcji
![2 2 f(x ) = log[(m + m − 6)x + (m − 2)x + 1]](https://img.zadania.info/zad/2939774/HzadT1x.gif)
jest zbiór wszystkich liczb rzeczywistych.
Wykaż, że wyrażenie 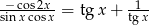 nie jest tożsamością.
nie jest tożsamością.
Dany jest wielomian 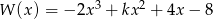 .
.
- Wyznacz wartość
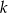 tak, aby reszta z dzielenia wielomianu W przez dwumian
tak, aby reszta z dzielenia wielomianu W przez dwumian 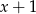 była równa -6.
była równa -6. - Dla znalezionej wartości
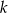 rozłóż wielomian na czynniki liniowe.
rozłóż wielomian na czynniki liniowe. - Dla znalezionej wartości
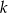 rozwiąż nierówność
rozwiąż nierówność 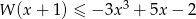 .
.
Reszta z dzielenia wielomianu 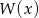 przez wielomian
przez wielomian 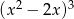 jest równa
jest równa 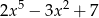 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 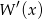 przez dwumian
przez dwumian 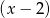 .
.
Oblicz granicę 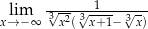 .
.
Reszta z dzielenia wielomianu 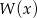 przez
przez 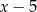 jest równa 4. Oblicz resztę z dzielenia wielomianu
jest równa 4. Oblicz resztę z dzielenia wielomianu 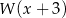 przez wielomian
przez wielomian 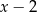 .
.
Reszta z dzielenia wielomianu 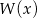 przez
przez 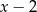 jest równa 7. Oblicz resztę z dzielenia wielomianu
jest równa 7. Oblicz resztę z dzielenia wielomianu 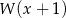 przez wielomian
przez wielomian 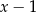 .
.
Wyznacz współczynniki 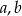 wielomianu
wielomianu 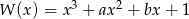 wiedząc, że dla każdego
wiedząc, że dla każdego 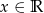 prawdziwa jest równość:
prawdziwa jest równość: 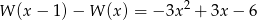 .
.

