Wielomiany 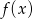 i
i 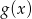 spełniają warunki
spełniają warunki 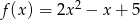 i
i 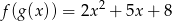 . Wyznacz wzór wielomianu
. Wyznacz wzór wielomianu 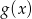 .
.
/Szkoła średnia/Funkcje
Sprowadź do postaci ogólnej funkcję kwadratową 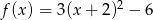 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 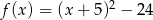 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 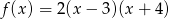 .
.
Zapisz wzór funkcji kwadratowej 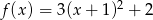 w postaci ogólnej.
w postaci ogólnej.
Sprowadź do postaci ogólnej funkcję kwadratową 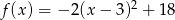 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 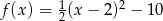 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 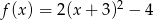 .
.
Wyznacz zbiór wartości funkcji określonej wzorem: 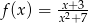 dla
dla 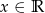 .
.
Uzasadnij, że jeżeli 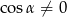 to prawdą jest, że
to prawdą jest, że 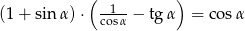 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to
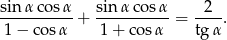
Wykaż, że dla każdego kąta ostrego  prawdziwy jest wzór
prawdziwy jest wzór 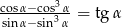 .
.
Wykaż, że 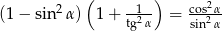 .
.
Wykaż tożsamość 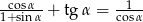 .
.
Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.
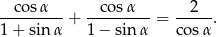
Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.
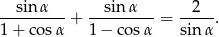
Wykaż, że 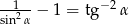 .
.
Uzasadnij, że dana równość 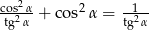 jest prawdziwa.
jest prawdziwa.
Właściciel pewnej pączkarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 40 kolejnych dni. Przyjmijmy, że liczbę 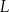 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
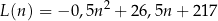
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 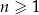 i
i 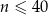 . Oblicz jaka była największa liczba klientów pączkarni obsłużonych jednego dnia w okresie poddanym analizie.
. Oblicz jaka była największa liczba klientów pączkarni obsłużonych jednego dnia w okresie poddanym analizie.
Przedstaw wielomian 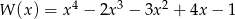 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
Wiesz, że funkcja kwadratowa 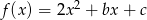 przyjmuje wartość najmniejszą
przyjmuje wartość najmniejszą 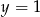 dla
dla 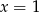 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 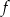 , a następnie rozwiąż równanie
, a następnie rozwiąż równanie 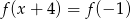 .
.
Kąt  jest ostry i
jest ostry i 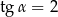 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 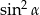 .
.
Dany jest wielomian 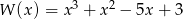 .
.
- Oblicz resztę z dzielenia tego wielomianu przez dwumian
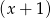 .
. - Oblicz miejsca zerowe tego wielomianu.
- Rozwiąż nierówność
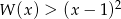 .
.
Nie wykonując dzielenia, wyznacz resztę z dzielenia wielomianu 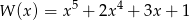 przez
przez 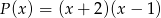 .
.
Dana jest funkcja 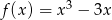 dla
dla 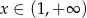 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 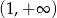 .
.
Wyznacz wartość największą i najmniejszą funkcji 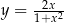 w przedziale
w przedziale 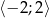 .
.
Wiedząc, że 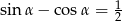 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 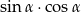 .
.
Wiedząc, że 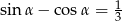 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 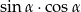 .
.
Wyznacz zbiór wartości funkcji 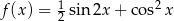 , gdzie
, gdzie 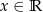 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 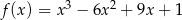 .
.
Wyznacz przedziały monotoniczności funkcji 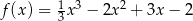 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 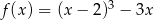 .
.
Dana jest funkcja 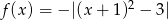 dla
dla 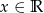 . Oblicz
. Oblicz 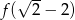 .
.
Dana jest funkcja 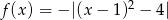 dla
dla 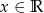 . Oblicz
. Oblicz 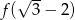 .
.
Wyznacz 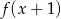 jeżeli
jeżeli 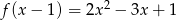 .
.
Oblicz granicę jednostronną 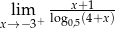 .
.
Oblicz granicę jednostronną 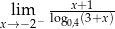 .
.
Wykaż, że nie istnieje kąt ostry  taki, że
taki, że 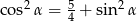 .
.
Dana jest funkcja 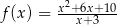 .
.
- Określ przedziały monotoniczności tej funkcji.
- Znajdź ekstrema lokalne funkcji
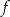 .
.

