Zbiornik na odpady płynne ma objętość 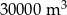 . Cykl pracy zbiornika obejmuje systematyczne jego napełnianie, co trwa 3 tygodnie, a następnie jego opróżnianie – trwa ono 3 dni. Opisz za pomocą wzoru ilość odpadów w zbiorniku w czasie pierwszego cyklu pracy. Oblicz, ile nieczystości znajduje się w zbiorniku w 254 dniu jego użytkowania?
. Cykl pracy zbiornika obejmuje systematyczne jego napełnianie, co trwa 3 tygodnie, a następnie jego opróżnianie – trwa ono 3 dni. Opisz za pomocą wzoru ilość odpadów w zbiorniku w czasie pierwszego cyklu pracy. Oblicz, ile nieczystości znajduje się w zbiorniku w 254 dniu jego użytkowania?
/Szkoła średnia/Zadania z treścią
Na przedstawienie sprzedano 200 biletów po 25 zł i 35 zł. Po potrąceniu 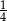 kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4650 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4650 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
Na przedstawienie sprzedano 300 biletów po 15 zł i 20 zł. Po potrąceniu 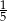 kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
Pole każdej z dwóch prostokątnych działek jest równe 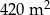 . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
. Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
Pole każdej z dwóch prostokątnych działek jest równe 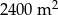 . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.
. Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.
Pusty zbiornik można zapełnić wodą z dwóch źródeł. Jeżeli będziemy nalewać wodę z pierwszego źródła przez 5 godzin, następnie zamkniemy to źródło i będziemy nalewać z drugiego przez 10 godzin, to zbiornik napełni się w 35%. Jeżeli natomiast będziemy napełniać zbiornik jednocześnie z dwóch źródeł, to zbiornik zostanie całkowicie napełniony w ciągu 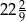 godzin. Ile godzin potrzeba do napełnienia całego zbiornika za pomocą każdego z źródeł osobno?
godzin. Ile godzin potrzeba do napełnienia całego zbiornika za pomocą każdego z źródeł osobno?
W rajdzie motocyklowym zawodnik, który zwyciężył, przejechał trasę z prędkością o 20 km/h większą niż drugi zawodnik i o 25 km/h większą od trzeciego zawodnika. Zawodnicy wystartowali jednocześnie. Na mecie drugi zawodnik był o 18 minut później niż zwycięzca i o 6 minut wcześniej niż trzeci zawodnik. Oblicz:
- długość trasy rajdu;
- prędkość jazdy każdego zawodnika;
- czasy przejazdu tych zawodników.
Cena produktu po podniesieniu stawki VAT z 7% do 22% wzrosła o 90 zł. Ile jest równa nowa cena produktu?
Ewa kupiła tablet za 480 zł oraz dodatkowe akcesoria w cenie 120 zł. Miesiąc później jej kolega Maciek kupił dokładnie taki sam tablet z akcesoriami, ale cena tabletu była o 10% niża, a cena akcesoriów wzrosła o 5%. O ile procent Maciek kupił swój zestaw taniej niż Ewa?
Liczbę dodatnią  przedstaw w postaci sumy dwóch takich składników, aby suma ich sześcianów była najmniejsza.
przedstaw w postaci sumy dwóch takich składników, aby suma ich sześcianów była najmniejsza.
Ile trzeba zmieszać roztworu wodnego soli kuchennej o stężeniu 26% z roztworem o stężeniu 4% żeby otrzymać 11 kg roztworu o stężeniu 18%?
Ile trzeba zmieszać roztworu wodnego soli kuchennej o stężeniu 20% z roztworem o stężeniu 8% żeby otrzymać 12 kg roztworu o stężeniu 13%?
- Suma kwadratów trzech kolejnych ujemnych liczb całkowitych parzystych jest równa 116. Wyznacz te liczby.
- Wyznacz takie trzy kolejne liczby całkowite parzyste, których suma kwadratów jest najmniejsza z możliwych.
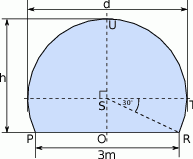
W architekturze islamu często stosowanym elementem był łuk podkowiasty. Schemat okna w kształcie takiego łuku (łuku okręgu) przedstawiono na rysunku poniżej. Korzystając z danych na rysunku oblicz wysokość okna 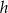 i największy prześwit
i największy prześwit 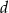 .
.
Przekrój betonowego kanału melioracyjnego ma kształt trapezu o podstawach 0,5 m i 1,5 m.
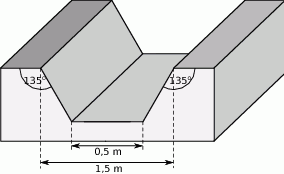
Oblicz ile wody zmieści się w takim kanale, jeżeli jego długość jest równa 50 m.
Przy jednoczesnej pracy 40 identycznych pomp nadmuchowych, żądany przepływ powietrza można zrealizować w ciągu 24 godzin. W ciągu ilu godzin można zrealizować ten sam przepływ powietrza przy jednoczesnej pracy 60 pomp?
Kowalski wpłacił na lokatę 10 000 zł, a po 4 latach przybyło 4641 zł odsetek (bez opodatkowania). Jakie bylo roczne oprocentowanie lokaty, jeżeli była ona kapitalizowana rocznie.
Właściciel sklepu kupił w hurtowni 30 książek i 20 poradników za 1020 zł. Poradniki sprzedał z zyskiem 20%, a książki z zyskiem 25%. W ten sposób zarobił 240 zł. Oblicz, w jakiej cenie sklepikarz kupił w hurtowni książki, a w jakiej poradniki.
Karol zarabiał miesięcznie 4200 zł, a Jan 3800 zł. Obaj otrzymali w swoich firmach podwyżki. Podwyżka otrzymana przez Jana była o 3 punkty procentowe wyższa niż podwyżka otrzymana przez Karola. Po podwyżce obaj panowie zarabiają łącznie 9074 zł. Ile zarabia każdy z panów po podwyżce? Zapisz wszystkie obliczenia.
Marcin zarabiał miesięcznie 3400 zł, a Adam 4300 zł. Obaj otrzymali w swoich firmach podwyżki. Podwyżka otrzymana przez Adama była o 4 punkty procentowe niższa niż podwyżka otrzymana przez Marcina. Po podwyżce obaj panowie zarabiają łącznie 8452 zł. Ile zarabia każdy z panów po podwyżce? Zapisz wszystkie obliczenia.
Ojciec i córka mają razem 50 lat. Pięć lat temu ojciec był 9 razy starszy od córki. Ile lat ma obecnie każde z nich.
Ojciec i syn mają łącznie 52 lata. Sześć lat temu ojciec był trzykrotnie starszy od syna. Ile lat ma ojciec, a ile syn?
Matka i córka mają łącznie 60 lat, a 10 lat temu matka był czterokrotnie starsza od córki. Ile lat ma matka, a ile córka?
Matka i córka mają łącznie 68 lat, a 8 lat temu matka był trzykrotnie starsza od córki. Ile lat ma matka, a ile córka?
Basia jest o 8 lat młodsza od Kasi. Za 30 lat będą miały razem 116 lat. Ile lat ma każda z nich obecnie?
Ojciec i syn mają łącznie 50 lat. Pięć lat temu ojciec był trzykrotnie starszy od syna. Ile lat ma ojciec, a ile syn?
Janek jest o 6 lat młodszy od Michała. Za 30 lat będą mieli razem 104 lata. Ile lat ma każdy z nich obecnie?
Roczne oprocentowanie lokaty, które wynosiło 6%, zmniejszono o 25%. Oblicz, o ile punktów procentowych zmniejszono to oprocentowanie.
Roczne oprocentowanie lokaty, które wynosiło 8%, zmniejszono o 37,5%. Oblicz, o ile punktów procentowych zmniejszono to oprocentowanie.
Mamy trzy roztwory, każdy zawierający chlorek sodu i chlorek potasu. Procentową zawartość obu chlorków w roztworach podano w tabeli.
| Roztwór | NaCl (chlorek sodu) | KCl (chlorek potasu) |
| I | 14,1% | 2,5% |
| II | 8,7% | 8,2% |
| III | 1,5% | 5,7% |
W jakim stosunku należy zmieszać wszystkie trzy roztwory, aby otrzymać roztwór, w którym stężenie każdego z chlorków wynosić będzie 6%?
Z krawędzi dachu podrzucono kamień, który po 2 sekundach spadł na ziemię. Wysokość (wyrażoną w metrach), na jakiej znajdował się kamień nad ziemią po upływie 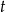 sekund od chwili jego podrzucenia, opisuje funkcja
sekund od chwili jego podrzucenia, opisuje funkcja 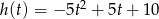 , gdzie
, gdzie 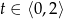 .
.
- Podaj, z jakiej wysokości (od ziemi) kamień został podrzucony.
- Oblicz, po jakim czasie od momentu podrzucenia kamień osiągnął największą wysokość.
- Oblicz największą wysokość (od ziemi), na jaką wzniósł się ten kamień.
Masa 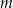 leku
leku 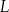 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
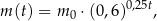
gdzie:
-
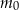 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 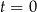 dawki leku,
dawki leku, -
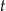 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 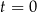 zażycia leku.
zażycia leku.
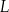 w dawce 200 mg. Oblicz, ile mg leku
w dawce 200 mg. Oblicz, ile mg leku 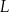 pozostanie w organizmie chorego po 12 godzinach od momentu przyjęcia dawki.
pozostanie w organizmie chorego po 12 godzinach od momentu przyjęcia dawki. Masa 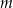 leku
leku 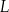 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
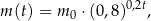
gdzie:
-
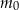 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 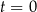 dawki leku,
dawki leku, -
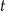 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 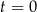 zażycia leku.
zażycia leku.
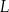 w dawce 300 mg. Oblicz, ile mg leku
w dawce 300 mg. Oblicz, ile mg leku 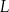 pozostanie w organizmie chorego po 15 godzinach od momentu przyjęcia dawki.
pozostanie w organizmie chorego po 15 godzinach od momentu przyjęcia dawki. 
