Gąsienica pełźnie po gałęzi do najbliższego smakowitego liścia, który jest odległy o 63,5 cm. Gąsienica jest jednak osłabiona i pełznie coraz wolniej. W pierwszej minucie udało jej się przebyć 32 cm, w drugiej pokonała drogę długości 16 cm, w trzeciej przepełznęła 8 cm itd. Po ilu minutach gąsienica dopełznie do liścia?
/Szkoła średnia/Zadania z treścią
Jacek wrzucał do skarbonki monety 10 groszowe, przy czym w sumie wrzucił do skarbonki 5,5 zł. Gdyby wrzucał monety ze średnią częstością o 10% większą, to czas potrzebny na wrzucenie wszystkich monet skróciłby się o 5 sekund. Oblicz, ile średnio monet na sekundę wrzucał Jacek do skarbonki.
Ukryj
Podobne zadania
Zosia wrzucała do rzeki kamyki, przy czym w sumie wrzuciła 36 kamyków. Gdyby wrzucała kamyki ze średnią częstotliwością o 20% większą, to czas potrzebny na wrzucenie wszystkich kamyków skróciłby się o 12 sekund. Oblicz, ile średnio kamyków na sekundę wrzucała Zosia do rzeki.
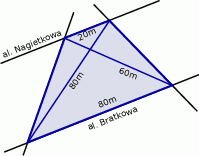
Działka budowlana Andrzeja ograniczona jest dwiema równoległymi alejami i dwoma innymi lokalnymi drogami. Andrzej zmierzył odcinki alei ograniczające działki (80 m i 20 m) oraz długości dwóch ścieżek znajdujących się na terenie tej działki, łączących jej przeciwległe rogi (80 m i 60 m). Następnie wykonał plan tej działki w skali 1:200 i wyznaczył pole powierzchni planu działki. Ile ono wynosiło?
Na podstawie zasad dynamiki można udowodnić, że torem ruchu rzuconej piłki – przy pominięciu oporów powietrza – jest fragment paraboli. Koszykarz wykonał rzut do kosza z odległości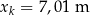 
, licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie 
, 
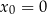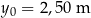. Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:
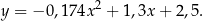
Rzut okazał się udany, a środek piłki przeszedł dokładnie przez środek kołowej obręczy kosza. Na rysunku poniżej przedstawiono tę sytuację oraz tor ruchu piłki w układzie współrzędnych.
W opisanym rzucie piłka przeleciała swobodnie przez obręcz kosza i upadła na parkiet. Przyjmij, że obręcz kosza nie miała siatki, a na drodze rzutu nie było żadnej przeszkody. Promień piłki jest równy 0,12 m. Oblicz współrzędną 
środka piłki w momencie, w którym piłka dotknęła parkietu. Wynik zapisz w metrach w zaokrągleniu do drugiego miejsca po przecinku.
Dwaj rzemieślnicy przyjęli zlecenie wykonania wspólnie 980 detali. Zaplanowali, że każdego dnia pierwszy z nich wykona 
, a drugi 
detali. Obliczyli, że razem wykonają zlecenie w ciągu 7 dni. Po pierwszym dniu pracy pierwszy z rzemieślników rozchorował się i wtedy drugi, aby wykonać całe zlecenie, musiał pracować o 8 dni dłużej niż planował, (nie zmieniając liczby wykonywanych codziennie detali). Oblicz 
i 
.
Drzewo rzuca cień o długości 11 m, a o tej samej porze cień chłopca o wzroście 170 cm ma długość 2,2 m. Oblicz wysokość drzewa.
Ukryj
Podobne zadania
Wieża rzuca cień o długości 31,5m. W tym samym czasie wbity pionowo w ziemię pręt o wysokości 1,6m rzuca cień o długości 1,2m. Oblicz wysokość wieży.
Wartość prędkości średniej obliczamy jako iloraz drogi i czasu, w którym ta droga została przebyta. Samochód przejechał z miejscowości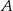 
do miejscowości 
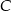przez miejscowość 
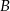, która znajduje się w połowie drogi z 
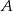do 
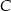. Wartość prędkości średniej samochodu na trasie z 
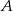do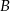 
była równa 40 km/h, a na trasie z 
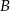do 
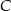– 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z 
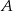do 
.
Ukryj
Podobne zadania
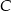Wartość prędkości średniej obliczamy jako iloraz drogi i czasu, w którym ta droga została przebyta. Samochód przejechał z miejscowości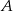 
do miejscowości 
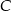przez miejscowość 
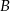, która znajduje się w 
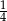drogi z 
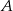do 
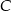. Wartość prędkości średniej samochodu na trasie z 
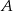do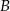 
była równa 80 km/h, a na trasie z 
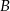do 
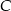– 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z 
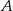do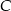 
.
Dana jest liczba dwucyfrowa. Jeśli dopiszemy na końcu tej liczby 5, to otrzymamy liczbę o 482 większą od danej. Jeśli zaś dopiszemy na końcu tej liczby dwucyfrowej 10, to otrzymamy liczbę o 5257 większa od danej. Wyznacz tę liczbę dwucyfrową.
Ukryj
Podobne zadania
Jeżeli na końcu liczby trzycyfrowej dopiszemy 23, to liczba ta zwiększy się o 43286. Jaka liczba trzycyfrowa ma tę własność?
Dane są dwie liczby dodatnie 
i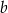 
, których stosunek wynosi 4:5. Jeżeli mniejszą z tych liczb zwiększymy o 25%, a większą zmniejszymy o 40, to stosunek otrzymanych liczb wyniesie 3:2. Oblicz wartość wyrażenia: 
.
Ukryj
Podobne zadania
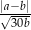Dane są dwie liczby dodatnie 
i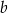 
, których stosunek wynosi 3:5. Jeżeli mniejszą z tych liczb zwiększymy o 18, a większą zmniejszymy o 55%, to stosunek otrzymanych liczb wyniesie 8:5. Oblicz wartość wyrażenia: 
.
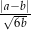Uczniowie klasy 3a napisali prace klasową z matematyki. Oceny bardzo dobre otrzymało 30% uczniów, oceny dobre 40% uczniów, oceny dostateczne 8 uczniów, a pozostali uczniowie otrzymali oceny dopuszczające. Średnia ocen z tej klasówki wynosiła 3,9. Ilu uczniów otrzymało poszczególne oceny?
Kasia przygotowując się do egzaminu rozwiązywała zadania w ciągu 3 dni. Pierwszego dnia rozwiązała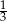 
zadań i jeszcze 4 zadania. Drugiego dnia połowę pozostałych i jeszcze 3 zadania. Trzeciego dnia pozostałych 17 zadań. Ile zadań rozwiązała w ciągu 3 dni?
Ania układa szklane kulki w figury pokazane na rysunku, na którym pokazane są pierwsze trzy figury.
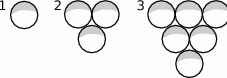
- Niech
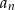będzie różnicą liczby kulek w 
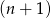–ej i 
–tej figurze. Wypisz pierwszych 5 wyrazów ciągu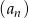 
. - Uzasadnij, że
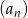jest ciągiem arytmetycznym i oblicz ile potrzeba kulek do ułożenia 20 figury.
Licznik ułamka jest o 3 mniejszy od mianownika. Jeżeli do tego ułamka dodamy jego odwrotność to otrzymamy 2,9. Znaleźć ten ułamek.
Ukryj
Podobne zadania
Mianownik ułamka jest dodatni i o 1 większy od licznika. Jeżeli do tego ułamka dodamy jego odwrotność to otrzymamy 2,05. Wyznacz ten ułamek.
Pociąg osobowy mija obserwatora w ciągu 5 s, a obok peronu długości 300 m przejeżdża w ciągu 25 s.
- Oblicz długość pociągu i jego prędkość.
- Określ, jak długo pociąg będzie mijał pociąg towarowy długości 150 m jadący równoległym torem w przeciwnym kierunku z prędkością 36 km/h.
Rafał wpłacił 300 zł do banku. Oprocentowanie w stosunku rocznym wynosi 12% i jest kapitalizowane miesięcznie. Ile pieniędzy wraz z odsetkami będzie miał po 9 miesiącach, zakładając, że oprocentowanie nie ulegnie zmianie?
Eksperymentalna kolonia bakterii liczyła przed 16 dniami 65536 bakterii, a obecnie liczy 390625 bakterii. O ile procent przeciętnie wzrasta liczba bakterii w tej kolonii w ciągu jednego dnia? (Zakładamy stały przyrost procentowy). Wynik podaj z dokładnością do 1%.
Pan Tomasz spłacił pożyczkę w wysokości 26760 zł w 24 ratach. Pierwsze 13 rat miało tą samą wysokość, a każda kolejna rata była o 60 zł mniejsza od poprzedniej. Oblicz kwotę pierwszej raty.
Oblicz sumę wszystkich liczb trzycyfrowych zapisanych wyłącznie za pomocą cyfr wybranych ze zbioru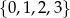 
.
Kasia i Tomek wyruszyli jednocześnie z tego samego domu do szkoły. Długość kroku Kasi jest o 12% mniejsza od kroku Tomka ale Kasia robi o 15% kroków więcej w tym samym czasie niż Tomek. Kto pierwszy dotrze do szkoły.
Chłopiec ma monety po 50 gr i po 20 gr, razem 27 sztuk. Monety mają łączną wartość 8,70 zł. Ile monet po 50 gr, a ile po 20 gr ma chłopiec?
Ukryj
Podobne zadania
Asia wrzucała do skarbonki monety dwu i pięciozłotowe. Po przeliczeniu zawartości skarbonki okazało się, że w skarbonce znajdowało się 395 monet, a uzbierana kwota wynosi 1195 złotych. Oblicz ile monet każdego rodzaju było w skarbonce.
Rozmieniono 34 złote na 116 monet, wśród których były tylko monety 50 i 20 groszowe. Ile było monet 50 groszowych?
