Pan Kowalski planując wyjazd na wakacje letnie w następnym roku postanowił założyć lokatę, wpłacając do banku 2000 zł na okres jednego roku. Ma do wyboru trzy rodzaje lokat:
-
lokata
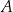 – oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku;
– oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku; -
lokata
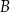 – oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku;
– oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku; -
lokata
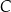 – oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.
– oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.
Oceń, wykonując odpowiednie obliczenia, która lokata jest najkorzystniejsza dla Pana Kowalskiego.

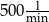 i jeden o wydajności
i jeden o wydajności 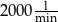 ?
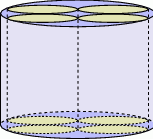
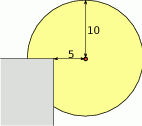
? 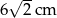 . Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze
. Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze 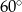 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 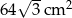 . Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.
. Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku. 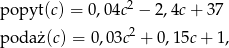
 –cena szynki w zł za kg i
–cena szynki w zł za kg i 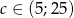 . Oblicz przy jakiej cenie szynki
. Oblicz przy jakiej cenie szynki 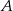 do przystani
do przystani 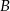 przez 40 minut, a wracała 56 minut. Oblicz prędkość motorówki i prędkość prądu rzeki, jeżeli przystanie
przez 40 minut, a wracała 56 minut. Oblicz prędkość motorówki i prędkość prądu rzeki, jeżeli przystanie 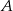 i
i 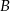 są odległe o 14 km.
są odległe o 14 km. 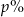 , końcowa cena stanowiła
, końcowa cena stanowiła 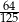 ceny początkowej. Oblicz
ceny początkowej. Oblicz 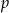 .
. 
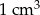 .
. 
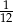 pożyczonej kwoty) i całości odsetek naliczonych w danym miesiącu od pozostającego do spłacenia kapitału.
pożyczonej kwoty) i całości odsetek naliczonych w danym miesiącu od pozostającego do spłacenia kapitału. 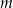 leku
leku 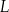 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą 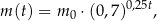
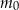 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 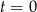 dawki leku,
dawki leku, 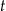 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 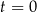 zażycia leku.
zażycia leku. w dawce 80 mg. Oblicz, po ilu godzinach od momentu przyjęcia dawki, w organizmie chorego pozostanie 39,2 mg leku
w dawce 80 mg. Oblicz, po ilu godzinach od momentu przyjęcia dawki, w organizmie chorego pozostanie 39,2 mg leku 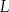 .
. 
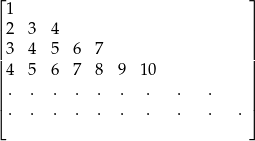
 -tego wiersza tablicy
-tego wiersza tablicy  w zależności od
w zależności od  .
. 
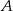 i
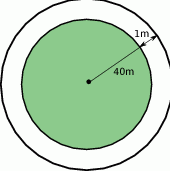
i 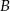 leżą po dwóch stronach jeziora. W terenie dokonano pomiarów odpowiednich kątów i ich wyniki przedstawiono na rysunku. Odległość między obiektami
leżą po dwóch stronach jeziora. W terenie dokonano pomiarów odpowiednich kątów i ich wyniki przedstawiono na rysunku. Odległość między obiektami 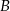 i
i 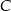 jest równa 400 m. Oblicz odległość w linii prostej między obiektami
jest równa 400 m. Oblicz odległość w linii prostej między obiektami 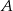 i
i 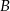 i podaj wynik, zaokrąglając go do jednego metra.
i podaj wynik, zaokrąglając go do jednego metra. 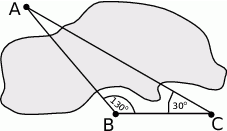
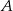 i
i 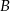 położonych od siebie w odległości 180 km. Rowerzysta jadący z miejscowości
położonych od siebie w odległości 180 km. Rowerzysta jadący z miejscowości 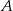 wyjechał o godzinę później od drugiego i jechał ze średnią prędkością 3 km/h mniejszą niż rowerzysta jadący z miejscowości
wyjechał o godzinę później od drugiego i jechał ze średnią prędkością 3 km/h mniejszą niż rowerzysta jadący z miejscowości 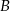 . Stosunek średnich prędkości rowerzystów wyrażał się liczbą z przedziału
. Stosunek średnich prędkości rowerzystów wyrażał się liczbą z przedziału 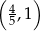 . Rowerzyści spotkali się w odległości 72 km od miejscowości
. Rowerzyści spotkali się w odległości 72 km od miejscowości 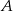 . Z jakimi średnimi prędkościami jechali obaj rowerzyści?
. Z jakimi średnimi prędkościami jechali obaj rowerzyści? 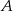 i
i 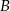 oddalonych od siebie o 182 km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości
oddalonych od siebie o 182 km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości 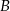 do miejscowości
do miejscowości 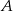 jedzie ze średnią prędkością mniejszą od 25 km/h. Rowerzysta jadący z miejscowości
jedzie ze średnią prędkością mniejszą od 25 km/h. Rowerzysta jadący z miejscowości 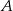 do miejscowości
do miejscowości 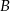 wyjeżdża o 1 godzinę wcześniej i jedzie ze średnią prędkością o 7 km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości
wyjeżdża o 1 godzinę wcześniej i jedzie ze średnią prędkością o 7 km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości 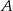 przebył do tego miejsca
przebył do tego miejsca 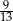 całej drogi z
całej drogi z 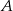 do
do 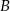 . Z jakimi średnimi prędkościami jechali obaj rowerzyści?
. Z jakimi średnimi prędkościami jechali obaj rowerzyści? 