Zadania z treścią/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Zadania z treścią

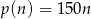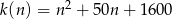W pewnym zakładzie pracy zależność przychodów ze sprzedaży od wielkości produkcji wyraża w przybliżeniu wzór p (n) = 150n , gdzie oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność k(n) = n2 + 50n + 1600 .

Napisz wzór funkcji 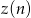- zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji.
Przy jakiej wielkości produkcji zysk wynosi 0?
Jaka wielkość produkcji zapewnia największy zysk? Jaki jest koszt produkcji, gdy zysk jest największy?

Ukryj Podobne zadania

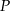Rodzinna ﬁrma stolarska produkuje małe wiatraki ogrodowe. Na podstawie analizy rzeczywistych wpływów i wydatków stwierdzono, że przychód (w złotych) z tygodniowej sprzedaży wiatraków można opisać funkcją

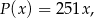
P (x) = 25 1x,

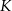a koszt (w złotych) produkcji wiatraków w ciągu jednego tygodnia można określić funkcją

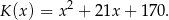
2 K (x) = x + 21x + 170.

Tygodniowo w zakładzie można wyprodukować co najwyżej 150 wiatraków. Oblicz, ile tygodniowo wiatraków należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk.

Zakład stolarski produkuje krzesła, które sprzedaje po 196 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:

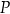przychód (w złotych) ze sprzedaży krzeseł można opisać funkcją
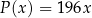
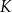koszt (w złotych) produkcji krzeseł dziennie można opisać funkcją

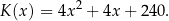
$K (x) = 4x 2 + 4x + 240.$

Dziennie w zakładzie można wyprodukować co najwyżej 30 krzeseł. Oblicz, ile krzeseł powinien dziennie sprzedawać zakład, aby zysk ze sprzedaży krzeseł wyprodukowanych przez ten zakład w ciągu jednego dnia był możliwie największy. Oblicz ten największy zysk.

Zakład stolarski produkuje stoły, które sprzedaje po 2144 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:

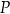przychód (w złotych) ze sprzedaży stołów można opisać funkcją
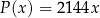
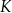koszt (w złotych) produkcji stołów miesięcznie można opisać funkcją

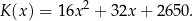
$K(x) = 16x2 + 32x + 26 50.$

Miesięcznie w zakładzie można wyprodukować co najwyżej 80 stołów. Oblicz, ile stołów powinien miesięcznie sprzedawać zakład, aby zysk ze sprzedaży stołów wyprodukowanych przez ten zakład w ciągu jednego miesiąca był możliwie największy. Oblicz ten największy zysk.

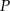Zakład ślusarski produkuje ozdobne kwietniki. Na podstawie analizy rzeczywistych wpływów i wydatków stwierdzono, że przychód (w złotych) z tygodniowej sprzedaży kwietników można opisać funkcją

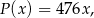
P (x) = 47 6x,

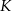a koszt (w złotych) produkcji kwietników w ciągu jednego tygodnia można określić funkcją

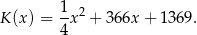
1 K (x) = -x2 + 366x + 1 369. 4

Tygodniowo w zakładzie można wyprodukować co najwyżej 250 kwietników. Oblicz, ile tygodniowo kwietników należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk.

Ania przeczytała książkę science-ﬁction, która miała 572 strony. Ania każdego dnia czytała o taką samą liczbę stron więcej, niż w dniu poprzednim. Ile dni Ania czytała tę książkę, jeżeli wiadomo, że w trzecim dniu Ania przeczytała 28 stron, a w ostatnim 68?

Dwóch braci pokonuje drogę z domu do szkoły pieszo. Młodszy potrzebuje na przebycie tej trasy 30 minut, a starszy 20 minut. Po ilu minutach starszy brat dogoni młodszego, jeśli wyjdzie z domu 5 minut po nim?

Ukryj Podobne zadania

Ala jeździ do szkoły rowerem, a Ola skuterem. Obie pokonują tę samą drogę. Ala wyjechała do szkoły o godzinie 7:00 i pokonała całą drogę w ciągu 40 minut. Ola wyjechała 10 minut później niż Ala, a pokonanie całej drogi zajęło jej tylko 20 minut. Oblicz, o której godzinie Ola wyprzedziła Alę.

W zbiorniku zamontowano dwie pompy: pierwsza z nich służy do napełniania zbiornika, a druga do jego opróżniania. Pierwsza pompa napełnia cały zbiornik w ciągu 30 minut, a druga opróżnia cały zbiornik w ciągu 20 minut. W pustym zbiorniku uruchamiamy pierwszą pompę, a po 5 minutach jej pracy uruchamiamy również drugą pompę. Po ilu minutach zbiornik będzie ponownie pusty?

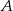Rowerzysta jedzie z miejscowości do odległej o 48 km miejscowości 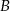. Gdyby zwiększył swoją prędkość o kilometrów na godzinę, to jechałby 4 godziny, gdyby zaś zmniejszył swoją prędkość o kilometrów na godzinę, to jechałby 6 godzin. Wyznacz prędkość rowerzysty.

Świeżo skoszona trawa zawiera 60% wody, a wysuszone siano tylko 15% wody. Oblicz, ile kilogramów wysuszonego siana można otrzymać z 1 tony skoszonej trawy? Wynik podaj w zaokrągleniu do pełnych kilogramów.

Stężenie pewnego roztworu wodnego soli wynosi 5%. Ile kilogramów czystej wody należy dodać do 90 kg tego roztworu, aby otrzymać roztwór o stężeniu 2%?

Ukryj Podobne zadania

Stężenie pewnego roztworu wodnego soli wynosi 10%. Ile kilogramów czystej wody należy dodać do 12 kg tego roztworu, aby otrzymać roztwór o stężeniu 6%?

Stężenie roztworu kwasu solnego wynosi 5%. Ile kilogramów wody należy dodać do 44 kg tego roztworu, aby stężenie roztworu zmniejszyło się do 2%?

Syzyf codziennie stoi przed zadaniem wtoczenia ciężkiej kamiennej kuli na szczyt pewnej góry.

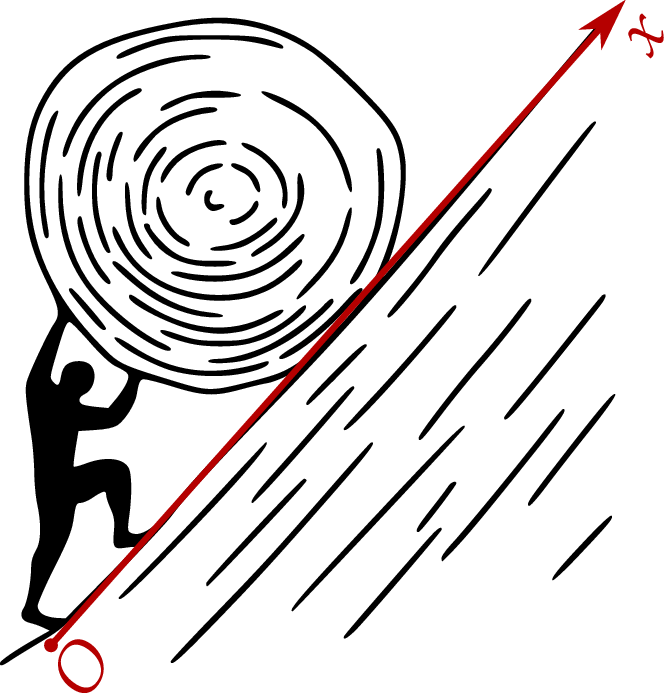
ZINFO-FIGURE

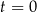W chwili t = 0 znajduje się on w punkcie 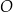oddalonym od szczytu o 4 km, a położenie Syzyfa wtaczającego kulę jest opisane zależnością

x (t) = −t3 + 16,5t2 + 180t dla t ∈ [0,24],

gdzie jest wyrażone w metrach, a 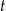– w godzinach. Oś 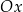jest skierowana do wierzchołka góry i jest styczna w każdym punkcie do zbocza góry. Oblicz najmniejszą odległość, na jaką Syzyf zbliży się do wierzchołka góry, oraz największą prędkość, z jaką wtacza kamień pod górę.

Wyznacz cztery kolejne liczby całkowite takie, że sześcian największej z nich jest równy sumie sześcianów trzech pozostałych liczb.

Ukryj Podobne zadania

Iloczyn trzech kolejnych liczb nieparzystych jest o 65 większy od różnicy kwadratów liczby największej i najmniejszej. Znajdź te liczby.

Ile kwadratowych płytek o boku 2 dm potrzeba do wyłożenia dna i wewnętrznych ścian basenu o długości 10 m, szerokości 6 m i głębokości 2 m ?

Ukryj Podobne zadania

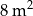Objętość prostopadłościennego basenu o szerokości 6 m i długości 10 m jest równa 120 000 litrów. Ile litrów farby potrzeba do pomalowania dna i ścian basenu, jeżeli jeden litr farby wystarcza do pomalowania 8 m 2 powierzchni?

Ile kwadratowych płytek o boku 3 dm potrzeba do wyłożenia dna i wewnętrznych ścian basenu o długości 9 m, szerokości 6 m i głębokości 3 m ?

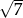Suma dwóch liczb jest równa √ -- 7 , a ich różnica 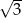√ -- 3 . Oblicz iloczyn tych liczb.

Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?

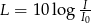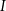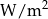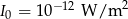Poziom natężenia dźwięku w decybelach jest opisany wzorem I- L = 1 0log I0 , gdzie jest natężeniem dźwięku wyrażonym w W/m 2 , a I0 = 10−12 W/m 2 jest stałą nazwaną natężeniem dźwięku odniesienia. Poziom natężenia szeptu wynosi 20 dB, a odpowiadające mu natężenie 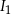jest 10000 razy mniejsze niż natężenie 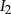pracującego odkurzacza. Oblicz poziom natężenia dźwięku w decybelach pracującego odkurzacza.

W fabryce zabawek znajduje się 10 maszyn do produkcji plastikowych samochodów. Średnia wydajność jednej maszyny wynosi 2100 samochodów dziennie. W okresie przedświątecznym uruchomiono jedną dodatkową maszynę, w wyniku czego średnia dzienna wydajność pojedynczego urządzenia zmalała o 4%. Oblicz ile samochodów dziennie produkuje dodatkowa maszyna.

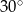Nachylenie stoku wynosi ∘ 30 , a długość stoku 150 m. Podaj różnicę wzniesień.

Ukryj Podobne zadania

Przymocowana do podłoża lina o długości 20 m podtrzymuje pionowy maszt. Na jakiej wysokości lina jest przymocowana do masztu jeżeli kąt nachylenia do powierzchni ziemi wynosi 60∘ ?

Przymocowana do podłoża lina o długości 16 m podtrzymuje pionowy maszt. Na jakiej wysokości lina jest przymocowana do masztu jeżeli kąt nachylenia do powierzchni ziemi wynosi 60∘ ?

W klasie liczba dziewcząt jest o 4 większa od liczby chłopców. Każdy chłopiec kupił kwiatek każdej koleżance z klasy. W sumie chłopcy kupili 221 kwiatków. Ilu uczniów liczy ta klasa?

Ukryj Podobne zadania

W klasie jest o 3 chłopców więcej niż dziewcząt. Na tłusty czwartek, każda z dziewcząt kupiła wszystkim chłopcom po jednym pączku. Razem kupiły 130 pączków. Ile osób liczy klasa?

Oblicz sumę wszystkich liczb naturalnych trzycyfrowych, których ostatnia cyfra jest równa 7.

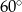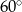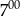Z tego samego miejsca wyruszyli w tę samą stronę piechur i rowerzysta. Piechur wyszedł o godzinie 700 i maszerował z prędkością 5 km/h, a rowerzysta wyjechał o godzinie 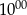1000 i jechał z prędkością 15 km/h. O której godzinie rowerzysta dogonił piechura?

Uzasadnij, że suma dwóch liczb dwucyfrowych takich, że cyfra dziesiątek i cyfra jedności pierwszej z nich jest odpowiednio cyfrą jedności i cyfrą dziesiątek drugiej jest podzielna przez 11.

Ukryj Podobne zadania

Uzasadnij, że różnica liczby dwucyfrowej i liczby o takich samych cyfrach, lecz zapisanych w odwrotnej kolejności, jest podzielna przez 9.

Cenę płaszcza zimowego obniżono wiosną o 15% i wówczas cena wynosiła 510 zł. Oblicz cenę płaszcza przed obniżką.

Malarz chcąc rozjaśnić 20 litrów granatowej farby postąpił w następujący sposób: odlał jeden litr farby i dolał 1 litr farby białej, a potem całość dokładnie wymieszał. Procedurę tę powtórzył w sumie 8 razy. Ile litrów granatowej farby pozostało w otrzymanej mieszaninie? Wynik podaj z dokładnością do 1 litra.

Strona 1 z 17