Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Zadania z treścią

Wyszukiwanie zadań

W chwili początkowej masa substancji jest równa 20 g. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 20% masy, jaka była na koniec doby poprzedniej. Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 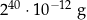40 − 12 2 ⋅10 g .

Obserwator stojący na płaskiej, poziomej powierzchni widzi pionową wieżę pod kątem 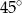45∘ , a po zbliżeniu się do niej o 20m pod kątem 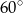60∘ . Oblicz wysokość wieży, wynik zaokrąglij do 1cm.

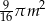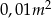Z kawałka materiału w kształcie czworokąta wypukłego o obwodzie 8m wycięto koło o polu 916πm 2 styczne do wszystkich boków czworokąta. Oblicz pole figury powstałej z tego czworokąta po wycięciu koła, z dokładnością do 0,01m 2 .

Pan Kwiatkowski i pan Kowalski wpłacili swoje oszczędności o łącznej wartości 10 000 zł do różnych banków. Pan Kwiatkowski ulokował swoje oszczędności w banku, w którym oprocentowanie rocznie wynosiło 12% zaś pan Kowalski - w banku, który proponował oprocentowanie roczne w wysokości 14%. Po roku łączna kwota odsetek wynosiła 1384 zł. Ile złotych ulokował w banku każdy z panów?

Rysunek przedstawia kształt obszaru zakreślanego przez wycieraczkę samochodową.

PIC

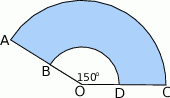
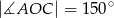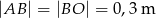Wiedząc, że |∡AOC | = 150∘ oraz |AB | = |BO | = 0,3 m oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że π ≈ 3 ,14 podaj wynik z dokładnością do 0,01 m .

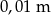W III wieku p.n.e władca Syrakuz, Hieron II, nakazał złotnikowi wykonać koronę ze sztaby ważącej 8,375 kg. Rzemieślnik wykonał koronę lecz władca podejrzewał, że artysta sprzeniewierzył część otrzymanego kruszcu. Hieron zwrócił się do Archimedesa, aby ten sprawdził, czy złotnik nie zastąpił części złota tańszym srebrem. Sławny fizyk zanurzył koronę w wodzie i sprawdził, że straciła ona pozornie na wadze 0,477 kg. Wiedząc, że złoto traci w wodzie pozornie 0,052 swojego ciężaru, z srebro 0,095, oblicz, ile złota, a ile srebra było w tej koronie. Wynik podaj z dokładnością do 0,001 kg.

Rejsowy samolot z Warszawy do Rzymu przelatuje nad Austrią każdorazowo tą samą trasą z taką samą zakładaną prędkością przelotową. We wtorek jego średnia prędkość była o 10% większa niż prędkość przelotowa, a w czwartek średnia prędkość była o 10% mniejsza od zakładanej prędkości przelotowej. Czas przelotu nad Austrią w czwartek różnił się od wtorkowego o 12 minut. Jak długo trwał przelot tego samolotu nad Austrią we wtorek?

Ukryj Podobne zadania

Pociąg pokonuje każdorazowo trasę pomiędzy Katowicami i Łodzią z taką samą zakładaną średnią prędkością. Pewnego dnia pociąg pokonał tę trasę w czasie o 10% krótszym od zakładanego, a następnego dnia w czasie o 15% dłuższym od zakładanego. Różnica prędkości średnich w tych dwóch dniach wyniosła 25 km/h. Ile wynosi zakładana średnia prędkość z jaką pociąg towarowy pokonuje trasę między Katowicami a Łodzią?

Rejsowy samolot z Warszawy do Paryża przelatuje nad Niemcami każdorazowo tą samą trasą z taką samą zakładaną prędkością przelotową. W poniedziałek jego średnia prędkość była o 20% mniejsza niż prędkość przelotowa, a w środę średnia prędkość była o 20% większa od zakładanej prędkości przelotowej. Czas przelotu nad Niemcami w poniedziałek różnił się od czasu przelotu w środę o 28 minut. Jak długo trwał przelot tego samolotu nad Niemcami w poniedziałek?

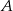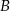Na zlecenie klienta makler ma kupić akcje spółek A i B za 1000 zł. Cena jednej akcji spółki 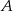A jest równa 4,25 zł, a jedna akcja spółki 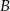B kosztuje 6,75 zł. Ile maksymalnie akcji każdego rodzaju makler może kupić, jeśli tańszych ma być o 10 więcej niż droższych?

Koszt godziny pływania pewnego rodzaju łodzi jest sumą kosztu stałego i kosztu zmiennego zależnego od prędkości łodzi. Wiadomo, że koszt stały jest równy 2880 zł/h, a koszt zmienny 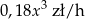0,18x 3 zł/h , gdzie 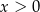x > 0 oznacza prędkość łodzi (w km/h).

  • Przy jakich prędkościach łodzi koszt przepłynięcia 1 km będzie mniejszy niż 306 zł?
  • Przy jakiej prędkości łodzi koszt przepłynięcia 1 km będzie najmniejszy? Oblicz ten koszt.

Zależność między temperaturą wyrażoną w stopniach Fahrenheita, a wyrażoną w stopniach Celsjusza jest zależnością liniową.

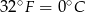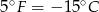  • Znajdź tę zależność wiedząc ze 3 2∘F = 0∘C , a 5∘F = − 15∘C .
  • 22 lipca w San Diego temperatura o godzinie 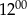12 00 była o 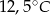1 2,5∘C wyższa niż temperatura o godzinie 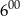00 6 . Wyraź wzrost temperatury w stopniach Fahrenheita.

Oblicz szerokość prostokątnej ramy obrazu wiedząc, że obwód zewnętrzny ramy jest o 28 cm większy od obwodu wewnętrznego tej ramy.

Kule o jednakowych promieniach ułożono w rzędach tworząc w ten sposób kwadrat. Gdyby usunięto 669 kul, to z pozostałych można by było zbudować trójkąt równoboczny (w pierwszym rzędzie jedna kula, w drugim dwie, w trzecim trzy itd.) Bok trójkąta równobocznego zawierałby wówczas o 8 kul więcej niż bok kwadratu. Z ilu kul zbudowany był kwadrat?

Złotnik ma dwie sztabki wykonane z różnych stopów. Pierwsza sztabka składa się ze 120 g złota i 30 g miedzi, a druga sztabka składa się ze 180 g złota i 20 g miedzi. Ile gramów każdej sztabki powinien wziąć złotnik, aby po stopieniu tych dwóch kawałków otrzymać sztabkę składającą się ze 172 g złota i 28 g miedzi?

Znajdź liczbę dwucyfrową wiedząc, że suma cyfr dziesiątek i jedności tej liczby jest równa 7, zaś różnica między szukaną liczbą i liczbą o tych samych cyfrach, lecz napisanych w odwrotnym porządku jest równa 27.

Ukryj Podobne zadania

Znajdź liczbę dwucyfrową wiedząc, że różnica między cyfrą dziesiątek, a cyfrą jedności tej liczby jest równa 3, oraz suma tej liczby i liczby powstałej przez zamianę miejscami jej cyfr jest równa 77.

Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 17. Jeśli zapiszemy cyfry tej liczby w przeciwnej kolejności, to otrzymamy liczbę o 99 większą od początkowej. Wyznacz liczbę początkową.

Ukryj Podobne zadania

Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 14. Jeśli zapiszemy cyfry tej liczby w przeciwnej kolejności, to otrzymamy liczbę o 198 większą od początkowej. Wyznacz liczbę początkową.

Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 15. Jeśli zapiszemy cyfry tej liczby w odwrotnej kolejności, to otrzymamy liczbę o 198 większą od początkowej. Wyznacz liczbę początkową.

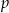Samochód jadący autostradą pali 5,6 litra paliwa na 100km. Napisz wzór funkcji s określającej przebytą drogę (w kilometrach) w zależnosci od zużytego paliwa p (w litrach).

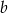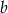Znajdź liczby a i b wiedząc, że suma liczby a i potrojonej liczby b jest równa 36, a iloczyn liczb a i b jest największy z możliwych.

W klasie na początku roku było 30 uczniów. W ciągu roku z klasy odeszło 20% dziewcząt i przybyło 60% chłopców. Na koniec roku liczba dziewcząt i chłopców w klasie była równa. Ile dziewcząt, i ilu chłopców liczyła klasa na początku roku?

Ukryj Podobne zadania

W pierwszym etapie konkursu matematycznego startowało 100 uczniów. Po pierwszym etapie z konkursu odpadło 50% dziewczynek oraz 15 chłopców. W drugim etapie konkursu wzięło udział trzy razy więcej chłopców niż dziewcząt. Ilu chłopców i ile dziewcząt wzięło udział w drugim etapie konkursu?

Strona 17 z 17