Zadania z treścią/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Zadania z treścią

Suma dwóch liczb równa jest 6. Znajdź te liczby, jeśli wiadomo, że suma podwojonego kwadratu jednej z nich i kwadratu drugiej jest najmniejsza z możliwych.

Rowerzysta jedzie ze stałą prędkością 20km/h.

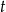Napisz wzór wyrażający drogę rowerzysty w ciągu godzin.
Sporządź tabelkę wartości dla .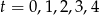
Naszkicuj wykres zależności od .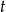

W tabeli umieszczono wynagrodzenie miesięczne 50 pracowników pewnej ﬁrmy:

Liczba pracowników	1	3	4	6	8	12	16
Wynagrodzenie	3600	2700	2100	2000	1750	1600	1450

Pracownicy ﬁrmy zarabiający mniej niż 2100zł otrzymali podwyżkę w wysokości 500zł, a pracownicy zarabiający powyżej 2000zł – podwyżkę w wysokości 20% średniego wynagrodzenia miesięcznego wszystkich pracowników. Ilu obecnie pracowników tej ﬁrmy zarabia więcej niż 3000zł?

Iloczyn cyfr liczby dwucyfrowej jest o 11 większy od sumy jej cyfr. Jeżeli przestawimy cyfry w tej liczbie, to otrzymamy liczbę o 36 większą od początkowej. Wyznacz tę liczbę.

Mariusz Czerkawski i Jimmy O’Brien w jednym sezonie NHL zdobyli w sumie 100 bramek. Kluby obu zawodników za każdą zdobytą bramkę wypłacały hokeistom z góry ustaloną premię. Po sezonie okazało się, że obaj zawodnicy otrzymali za strzelone bramki równe kwoty. Gdyby Czerkawski zdobył tyle bramek ile O’Brien, to otrzymałby 72000$, zaś gdyby drugi strzelił tyle bramek ile pierwszy, to otrzymałby 32000$. Oblicz, ile bramek zdobył każdy z nich i jaka była wysokość premii w obu klubach za strzelenie bramki.

Dziesięć kul bilardowych średnicy 6 cm umieszczono w prostokątnym pudełku tak jako pokazano to na rysunku.

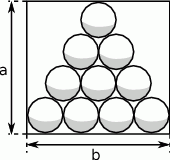
Wyznacz wymiary i 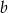tego pudełka.

Dzienny dochód hurtowni akumulatorów wyraża się wzorem 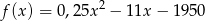f (x) = 0,25x 2 − 11x − 1950 , gdzie oznacza liczbę sprzedanych akumulatorów.

Oblicz przy jakiej liczbie sprzedanych akumulatorów ﬁrma poniesie największą stratę. Oblicz wartość tej straty.
Oblicz ile akumulatorów należy sprzedać, aby dzienny dochód wynosił 4985.

Wyprowadź wzór 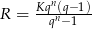Kqn(q−1) R = qn−1 na wysokość raty 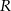kredytu udzielonego w kwocie 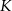, przy założeniu, że:
– spłata tego kredytu jest rozłożona na równych rat płaconych miesięcznie;
– pierwszą ratę wpłacamy po miesiącu od daty udzielenia kredytu;
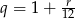– roczne oprocentowanie kredytu jest równe i r- q = 1+ 12 .

Mały Antek założył zeszyt, w którym każdego dnia zapisuje jedną liczbę. Pierwszą zapisaną przez niego liczbą było 112, a każdego następnego dnia zmniejsza wpisywaną liczbę o 7.

Przez ile dni Antek wpisywał do zeszytu liczby, jeżeli wśród wpisanych liczb są liczby ujemne, a suma wszystkich liczb wynosi 805.
Ile liczb dodatnich jest wpisanych do zeszytu?

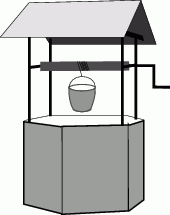
Wiadro wisi przywiązane do łańcucha nawiniętego na wałek kołowrotu tak, jak przedstawiono na rysunku. Aby wiadro dotknęło lustra wody należy wykonać 14 pełnych obrotów korbą. Oblicz odległość lustra wody od brzegu studni, gdy wiadomo, że wałek kołowrotu ma średnicę 20 cm. Wynik podaj w zaokrągleniu do 1 m.

Skala Richtera służy do określania siły trzęsień ziemi. Siła ta opisana jest wzorem 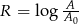R = log AA0- , gdzie 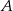oznacza amplitudę trzęsienia wyrażoną w centymetrach, 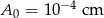A = 10− 4 cm 0 jest stałą, nazywaną amplitudą wzorcową. 5 maja 2014 roku w Tajlandii miało miejsce trzęsienie ziemi o sile 6,2 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Tajlandii i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 cm.

Ukryj Podobne zadania

Skala Richtera służy do określania siły trzęsień ziemi. Siła ta opisana jest wzorem 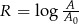R = log AA0- , gdzie 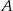oznacza amplitudę trzęsienia wyrażoną w centymetrach, 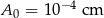A = 10− 4 cm 0 jest stałą, nazywaną amplitudą wzorcową. 27 lutego 2010 roku w Chile miało miejsce trzęsienie ziemi o sile 8,8 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Chile i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 m.

Huta szkła produkuje kulki szklane o promieniu 5 cm. Do wysyłki będą one pakowane po 4 sztuki w sztywne pudełka w kształcie walca, którego wysokość wynosi 10 cm, a średnica 24 cm. Czy dobrze została dobrana średnica tych pudełek?

Kuba pożyczył od taty samochód, którym wyruszył z domu na spotkanie ze swoją dziewczyną. Przed wyjazdem obliczył, że jadąc ze średnią prędkością 60 km/h przybędzie na spotkanie dokładnie o umówionej godzinie. Po przejechaniu (z zaplanowaną prędkością) 60% drogi "złapał gumę", a zmiana koła zajęła mu 16 minut. Teraz, aby zdążyć na spotkanie, musiałby jechać z prędkością 120 km/h. Oblicz odległość od domu Kuby do miejsca spotkania z ukochaną.

Klasa IIIb liczy o jednego ucznia więcej niż klasa IIIa. Na koniec roku okazało się, że suma ocen z matematyki uzyskanych przez uczniów klasy IIIa jest równa 97,5 i jest jednocześnie równa sumie ocen z matematyki uzyskanych przez uczniów klasy IIIb. Gdy obliczono średnie z tych ocen w każdej z klas to okazało się, że średnia w klasie IIIa była wyższa o 0,15 niż średnia uzyskana w klasie IIIb. Oblicz ilu uczniów liczą obie klasy.

Czy kwadratowe lustro o boku długości 2,2 m można przenieść przez drzwi o szerokości 1 m i wysokości 2 m?

Cenę sukienki obniżano dwukrotnie, za każdym razem o ten sam procent. W wyniku tych obniżek cena sukienki ze 100 zł spadła do 96,04 zł. Oblicz, o ile procent za każdym razem obniżano cenę sukienki.

Z miast odległych o 52 km o godzinie 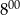00 8 wyjechali naprzeciw siebie dwaj rowerzyści. Każdy z nich jechał ze stałą prędkością. Prędkość jazdy jednego z nich wynosiła 15 km/h. Ile wynosi prędkość jazdy drugiego rowerzysty, jeżeli spotkali się o godzinie 9 20 ?

Ukryj Podobne zadania

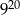Z miast odległych o 45 km o godzinie 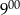00 9 wyjechali naprzeciw siebie dwaj rowerzyści. Każdy z nich jechał ze stałą prędkością. Prędkość jazdy jednego z nich wynosiła 12 km/h. Ile wynosi prędkość jazdy drugiego rowerzysty, jeżeli spotkali się o godzinie 1 015 ?

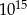Oblicz sumę tych liczb naturalnych, które przy dzieleniu przez 4 dają resztę 3 i są mniejsze od 300.

Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.

Ukryj Podobne zadania

Po zmodernizowaniu linii kolejowych przeciętna prędkość pociągów ekspresowych kursujących na 400-kilometrowej trasie wzrosła o 20 km/godz, a czas podróży skrócił się o godzinę. Oblicz, z jaką średnia prędkością jeżdżą obecnie pociągi ekspresowe na tej trasie.

Turysta przeszedł trasę długości 24 km ze stałą prędkością. Gdyby prędkość tę zwiększył o 1,2 km/h, to tę samą drogę przeszedłby w czasie o 1 godzinę krótszym. Oblicz rzeczywistą prędkość turysty i czas, w którym przebył trasę.

Samochód przebył w pewnym czasie 210 km. Gdyby jechał o pół godziny krócej to średnia prędkość z jaką przejechał tę trasę byłaby większa o 10 km/h. Oblicz, z jaką średnią prędkością jechał ten samochód.

Samochód przejechał trasę długości 84 km. Gdyby jechał ze średnią prędkością większą o 12 km/h, to przejechałby tę trasę w czasie o 21 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten samochód.

Kierowca obliczył, że trasę 220 km pokona w czasie 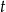, jeśli będzie jechał ze średnią prędkością . Wyjechał o 20 minut później niż zamierzał, więc aby dojechać na zaplanowaną godzinę, musiał zwiększyć prędkość o 5 km/h. Oblicz średnią prędkość z jaką planował jechać kierowca.

Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 36 minut.

Kolarz pokonał trasę 114 km. Gdyby jechał ze średnią prędkością mniejszą o 9,5 km/h, to pokonałby tę trasę w czasie o 2 godziny dłuższym. Oblicz, z jaką średnią prędkością jechał ten kolarz.

Pewien kierowca, jadąc z miasta 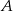do miasta 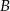, zmierzył czas i prędkość jazdy. Drogę powrotną pokonał z prędkością o 12 km/h większą, w czasie o 12 minut krótszym. Z jaką średnią prędkością wracał kierowca do miasta , jeżeli wiadomo, że miasta te są oddalone od siebie o 117 km?

Grupa rowerzystów jechała ze stałą prędkością do miasta oddalonego o 120 km. Gdyby jechali ze średnią prędkością o 5 km/godz. większą, to przejechaliby tę odległość w czasie o 2 godziny krótszym. Wyznacz średnią prędkość grupy i czas przejazdu.

Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 24 minut.

Kolarz przejechał trasę długości 60 km. Gdyby jechał ze średnią prędkością większą o 1 km/h, to przejechałby tę trasę w czasie o 6 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten kolarz.

Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 60 km. Jadąc z domu nad jezioro poruszał się z prędkością o 2 km/h większą niż w drodze powrotnej i pokonał trasę w czasie o 10 minut krótszym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?

Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 80 km. Jadąc z domu nad jezioro poruszał się z prędkością o 4 km/h mniejszą niż w drodze powrotnej i pokonał trasę w czasie o 20 minut dłuższym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?

Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?

Strona 16 z 17