Zadania z treścią/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Zadania z treścią

Liczbę przedstaw w postaci różnicy dwóch liczb tak, aby suma kwadratów tych liczb była najmniejsza.

Jeden z boków prostokąta zwiększono o 10%, a drugi zmniejszono o 10%. Czy pole tego prostokąta uległo zmianie? Jeżeli tak, to o ile procent?

Ukryj Podobne zadania

Dany jest prostokąt o bokach i 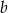. Długość boku zmniejszono o 20% a długość boku 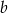zwiększono o 10%. Oblicz, ile procent pola prostokąta o bokach i 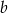stanowi pole prostokąta otrzymanego po dokonaniu zmian długości boków.

Zakład rzemieślniczy otrzymał zlecenie wykonania partii detali. Do realizacji tego zamówienia wyznaczono trzy stanowiska tokarskie, przy czym wydajność stanowisk drugiego i trzeciego była odpowiednio o 20% i 40% mniejsza niż wydajność stanowiska pierwszego. Proces produkcji detali miał trwać 20 dni, ale po 13 dniach pierwsza tokarka uległa uszkodzeniu i proces produkcyjny dokończono przy pomocy dwóch pozostałych stanowisk. O ile dni wydłużyła się realizacja zamówienia?

Większa część uczniów klasy liczącej 31 osób zachorowała na grypę. Zdrowi uczniowie postanowili wysłać chorym kolegom kartki z pozdrowieniami. Wiedząc, że każdy zdrowy uczeń wysłał do każdego chorego kolegi kartkę oraz, że liczba wysłanych kartek była największa z możliwych, oblicz ilu uczniów zachorowało na grypę.

Rowerzysta w ciągu pierwszej godziny przejechał 21 km, a w ciągu każdej następnej godziny – odcinek o 0,75 km krótszy od poprzedniego. Jaką drogę pokonał rowerzysta i w jakim czasie, jeśli w ciągu ostatniej godziny przejechał 18 km?

Pan Piotrek postanowił założyć lokatę, wpłacając 10000 zł na okres jednego roku. Bank proponuje oprocentowanie kapitału 12% w stosunku rocznym, z kapitalizacją odsetek co kwartał. Oblicz, jaką kwotę będzie dysponować pan Piotrek po roku, wiedząc, że podatek od uzyskanego w ten sposób dochodu wynosi 19% i jest pobierany przy każdej kapitalizacji.

Z dwóch miast 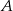i 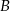, odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta 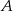o jedną godzinę wcześniej niż drugi z miasta 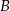. Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta 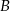jeszcze 1,5 godziny, drugi zaś szedł jeszcze 4 godziny do miasta .

Ukryj Podobne zadania

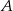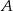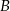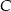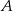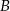Z dwóch miast i odległych od siebie o 90 km wyjechali rowerami dwaj znajomi, by spotkać się o umówionej godzinie w miejscowości , znajdującej się między i . Pierwszy (z 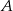) wyjechał o godzinę później niż drugi. W jakiej odległości od 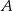znajduje się 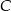, jeśli wiemy, że gdyby znajomi kontynuowali podróż (po spotkaniu w 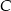), każdy w wybranym wcześniej kierunku i z dotychczasową szybkością, to pierwszy dotarłby do 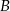po półtorej godziny, zaś drugi do 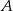– po 4 godzinach?

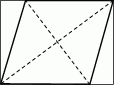
Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?

Pan Adam wpłacił na rachunek w funduszu inwestycyjnym pewną kwotę pieniędzy. Po roku stan rachunku zwiększył się o 4,5%, w drugim roku zmniejszył się o 5%, a w trzecim roku wzrósł o 4%. Wiedząc, że stan rachunku pana Adama po trzech latach oszczędzania wynosi 1548,69 zł oblicz jaką kwotę pan Adam początkowo wpłacił na ten rachunek.

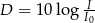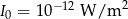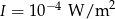Głośność (w dB) obliczamy ze wzoru -I D = 10 log I0 , gdzie −12 2 I0 = 1 0 W/m . Oblicz głośność krzyku niemowlencia, dla którego I = 10− 4 W/m 2 .

Dwaj rowerzyści pokonują trasę między punktam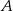i i 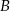. O ile procent średnia prędkość drugiego rowerzysty musi być większa od średniej prędkości pierwszego rowerzysty, aby przyjechał on o 20% szybciej?

Właściciel sklepu z odzieżą kupił w hurtowni koszulki, płacąc za nie 720 zł. Gdyby każda koszulka kosztowała o 2 złote mniej, to za tę samą kwotę mógłby kupić o 5 koszulek więcej. Oblicz, ile koszulek kupił w tej hurtowni wspomniany właściciel sklepu. Podaj cenę jednej koszulki.

Ukryj Podobne zadania

Obecnie 1 kg cukru kosztuje o 3,20 zł więcej niż kilka lat temu. Wówczas za kwotę równą 225 zł można było kupić o 80 kg więcej cukru niż obecnie. Ile kosztuje 1 kg cukru obecnie?

W roku 2005 na uroczystości urodzin zapytano jubilata, ile ma lat. Jubilat odpowiedział: „Jeśli swój wiek sprzed 10 lat pomnożę przez swój wiek za 11 lat, to otrzymam rok mojego urodzenia". Ułóż odpowiednie równanie, rozwiąż je i zapisz, w którym roku urodził się ten jubilat.

Ukryj Podobne zadania

W roku 2015 na uroczystości urodzinowej ktoś zapytał jubilata, które urodziny obchodzi. Jubilat odpowiedział: jeżeli mój wiek sprzed 27 lat pomnożysz przez mój wiek za 15 lat, to otrzymasz rok mojego urodzenia. Oblicz, ile lat ma ten jubilat.

W roku 2016 na uroczystości urodzinowej ktoś zapytał jubilata, które urodziny obchodzi. Jubilat odpowiedział: jeżeli mój wiek sprzed 36 lat pomnożysz przez mój wiek za 55 lat, to otrzymasz rok mojego urodzenia. Oblicz, ile lat ma ten jubilat.

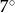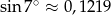Przed wejściem do przychodni lekarskiej znajdują się schody mające 8 stopni po 15 cm wysokości każdy. Obok schodów jest podjazd dla niepełnosprawnych o nachyleniu . Oblicz długość podjazdu. Wynik podaj w zaokrągleniu do 10 cm. ( sin 7∘ ≈ 0,1 219 )

Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 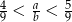49 < ab < 59 .

Ukryj Podobne zadania

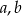Podaj przykład liczb całkowitych a,b , dla których prawdziwa jest nierówność podwójna:

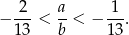
− -2-< a-< − 1-. 13 b 13

Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 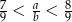79 < ab < 89 .

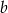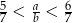Podaj przykład liczb całkowitych dodatnich i , spełniających nierówność 57 < ab < 67 .

Po torze wodnym o długości 10 km pływają w kółko dwie łodzie motorowe, przy czym druga z nich płynie z prędkością o 5 km/h większą od prędkości pierwszej łodzi. Łodzie te wystartowały z tego samego punktu i ponownie spotkały się, gdy pierwsza z łodzi wykonała pełne 3 okrążenia toru. Oblicz średnie prędkości obu łodzi.

Ukryj Podobne zadania

Trasa rowerowa wokół jeziora ma długość 12 kilometrów. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro w tym samym kierunku. Średnia prędkość jednego z nich jest o 4 km/h mniejsza niż prędkość drugiego rowerzysty. Do ponownego spotkania rowerzystów doszło, gdy szybszy z nich wykonał 4 okrążenia jeziora. Jakie były średnie prędkości rowerzystów?

Firma obuwnicza otrzymała zamówienie na wykonanie 720 par butów. Aby zrealizować zamówienie na czas, postanowiono wykonywać dziennie jednakową liczbę par butów. Po wykonaniu 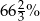6623 % zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 4 pary, zaś zamówienie zrealizowano o 5 dni wcześniej. W ciągu ilu dni planowano wykonać zamówienie?

Ukryj Podobne zadania

Firma odzieżowa otrzymała zamówienie na wykonanie 600 kurtek. Aby zrealizować zamówienie ﬁrma postanowiła wykonywać dziennie tę samą liczbę kurtek. Po wykonaniu 60% zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 6 kurtek, zaś zamówienie zrealizowano o 2 dni wcześniej w stosunku do pierwotnego planu. W ciągu ilu dni zrealizowano zamówienie?

W chwili początkowej (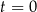 t = 0 ) zainicjowano pewną reakcję chemiczną, w której brał udział związek 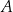. W wyniku tej reakcji masa 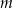związku 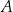zmieniała się w czasie zgodnie z zależnością

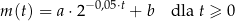
m (t) = a⋅2− 0,05⋅t + b dla t ≥ 0

gdzie:

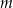– masa związku 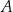wyrażona w gramach,
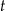– czas wyrażony w sekundach (liczony od chwili ),
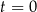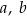– współczynniki liczbowe.

Masa początkowa związku 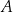(tj. masa w chwili 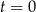t = 0 ) była równa 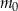m 0 gramów. Po osiągnięciu stanu równowagi (tj. gdy 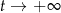t → + ∞ ) masa tego związku była równa 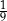1 9 jego masy początkowej (zobacz rysunek).

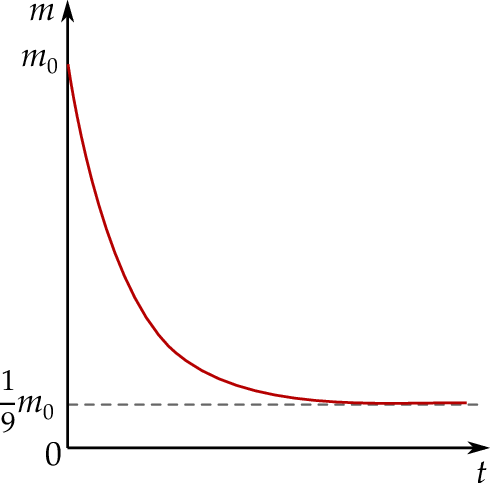
Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało 87,5% masy początkowej tego związku.

Ewa jadąc drogą widziała elektrownię wiatrową oznaczoną na rysunku literą . Z punktu 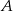widziała ją pod kątem 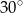30∘ stopni do kierunku drogi. A z punktu 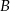pod kątem 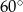60∘ . Przejeżdżając przez punkt 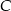minęła elektrownię. Długość odcinka 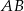jest równa 20km.

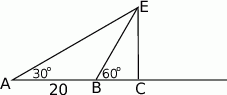
Oblicz miary kątów 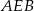i .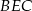
Oblicz długość odcinka .
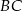Oblicz odległość elektrowni od drogi.

W rachunkach przyjmij, że 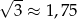√ -- 3 ≈ 1,75 .

Zosia przez 30 dni kwietnia wrzucała do skarbonki pieniądze, przy czym każdego kolejnego dnia wrzucała o 2 zł więcej niż w dniu poprzednim. Wiedząc, że średnio wrzucała 33 zł złotych dziennie, oblicz ile pieniędzy wrzuciła do skarbonki 8 kwietnia.

Strona 15 z 17