Kostki pozbruku mają kształt graniastosłupów prawidłowych sześciokątnych.
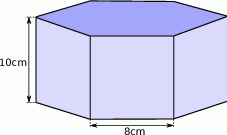
- Jaka jest powierzchnia całkowita jednej kostki?
- Jaką ilość betonu (w
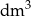 ) zużyto do wyprodukowania 100 takich kostek? Wyniki podaj z dokładnością do 0,01.
) zużyto do wyprodukowania 100 takich kostek? Wyniki podaj z dokładnością do 0,01.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kostki pozbruku mają kształt graniastosłupów prawidłowych sześciokątnych.

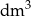 ) zużyto do wyprodukowania 100 takich kostek? Wyniki podaj z dokładnością do 0,01.
) zużyto do wyprodukowania 100 takich kostek? Wyniki podaj z dokładnością do 0,01.W dwóch naczyniach jest woda. Gdyby z pierwszego naczynia przelano do drugiego 2 litry wody, to w obu naczyniach byłoby jej tyle samo. Gdyby zaś z drugiego do pierwszego przelano 3 litry wody, to w pierwszym naczyniu byłoby jej sześć razy więcej niż w drugim. Ile jest wody w obu naczyniach?
W pierwszym zbiorniku było cztery razy więcej litrów wody niż w drugim. Do każdego zbiornika wlano po 6 litrów wody. Teraz w pierwszym zbiorniku jest dwa razy więcej litrów wody niż w drugim zbiorniku. Oblicz, ile łącznie litrów wody jest w obu zbiornikach.
Trawnik ma kształt trójkąta równoramiennego o podstawie 80 m i ramionach długości 50 m. Z powierzchni trawnika postanowiono wydzielić prostokątny plac zabaw w ten sposób, że dwa z wierzchołków tego prostokąta leżą na podstawie, a pozostałe dwa na ramionach trójkąta ograniczającego trawnik (zobacz rysunek).
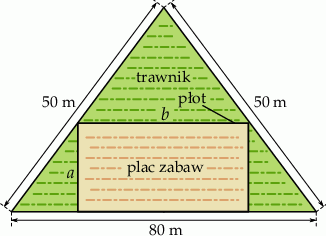
Oblicz wymiary  i
i 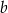 placu zabaw, tak, aby jego pole było największe możliwe.
placu zabaw, tak, aby jego pole było największe możliwe.
Olejarnia wytwarza olej ekologiczny. Aby produkcja była opłacalna, dzienna wielkość produkcji musi wynosić co najmniej 480 litrów i nie może przekroczyć 530 litrów (ze względu na ograniczone moce produkcyjne). Przy poziomie produkcji 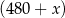 litrów dziennie przeciętny koszt
litrów dziennie przeciętny koszt 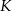 (w złotych) wytworzenia jednego litra oleju jest równy
(w złotych) wytworzenia jednego litra oleju jest równy
![22x 2 − 62 1,5x + 23430 K(x ) = -----------------------, gdzie x ∈ [0,50] 480+ x](https://img.zadania.info/zad/8271275/HzadT2x.gif)
Oblicz, ile litrów oleju dziennie powinna wytworzyć olejarnia, aby przeciętny koszt produkcji jednego litra oleju był najmniejszy (z zachowaniem opłacalności produkcji). Oblicz ten najmniejszy przeciętny koszt.
Linia produkcyjna w fabryce elektroniki wytwarza jeden rodzaj kart graficznych. Aby produkcja była opłacalna, dzienna wielkość produkcji musi wynosić co najmniej 576 kart i nie może przekroczyć 620 kart (ze względu na ograniczone moce produkcyjne). Przy poziomie produkcji 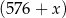 kart graficznych dziennie przeciętny koszt
kart graficznych dziennie przeciętny koszt 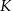 (w złotych) wytworzenia jednej karty jest równy
(w złotych) wytworzenia jednej karty jest równy
![2 K (x) = 2-3x-−--103,5x-+-42-4764, gdzie x ∈ [0,44] 576+ x](https://img.zadania.info/zad/3502777/HzadT2x.gif)
Oblicz, ile kart graficznych powinna wytwarzać dziennie ta linia produkcyjna, aby przeciętny koszt produkcji jednej karty był najmniejszy (z zachowaniem opłacalności produkcji). Oblicz ten najmniejszy przeciętny koszt.
W pewnej klasie liczba dziewcząt stanowi 60% liczby osób w tej klasie. Gdy 6 dziewcząt wyjechało na mecz siatkówki, w klasie pozostało tyle samo chłopców, ile dziewcząt. Oblicz, ile osób liczy ta klasa oraz ilu jest w niej chłopców.
W pewnej klasie liczba chłopców stanowi 75% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze czterech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
W pewnej klasie liczba chłopców stanowi 60% liczby wszystkich uczniów. Gdyby 6 chłopców przeniosło się do innej klasy, w klasie pozostałoby po tyle samo dziewcząt i chłopców. Oblicz ile osób liczy ta klasa oraz ile jest w niej dziewcząt.
W pewnej klasie liczba chłopców stanowi 80% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze trzech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
W pewnej klasie liczba dziewcząt stanowi 60% liczby wszystkich uczniów. Gdyby 6 dziewcząt przeniosło się do innej klasy, w klasie pozostałoby po tyle samo dziewcząt i chłopców. Oblicz ile osób liczy ta klasa oraz ile jest w niej chłopców.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy połowę jego licznika, to otrzymamy 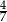 , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 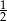 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika i do mianownika dodatniego ułamka dodamy jego licznik, to otrzymamy  , a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy 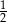 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy jego licznik, to otrzymamy 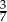 , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 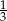 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy jego licznik, to otrzymamy 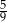 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika pewnego nieskracalnego ułamka dodamy 32, a mianownik pozostawimy niezmieniony, to otrzymamy liczbę 2. Jeżeli natomiast od licznika i od mianownika tego ułamka odejmiemy 6, to otrzymamy liczbę 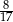 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Dany jest dodatni ułamek nieskracalny. Jeżeli dodamy do licznika ułamka 20% mianownika, a następnie od mianownika odejmiemy 20% zmienionego licznika, to otrzymamy 1,25. Jeżeli natomiast do mianownika danego ułamka dodamy 25% licznika, a od licznika odejmiemy 1, to otrzymamy 0,5. Wyznacz ten ułamek.
Jeżeli do licznika pewnego nieskracalnego ułamka dodamy 45, a mianownik pozostawimy niezmieniony, to otrzymamy liczbę 2. Jeżeli natomiast od licznika i od mianownika tego ułamka odejmiemy 3, to otrzymamy liczbę 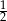 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po  okresach rozpadu połowicznego wyraża się wzorem
okresach rozpadu połowicznego wyraża się wzorem 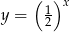 .
.
W przypadku izotopu jodu 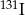 czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g
czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g 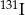 nie więcej niż 0,125 g tego pierwiastka.
nie więcej niż 0,125 g tego pierwiastka.
Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po  okresach rozpadu połowicznego wyraża się wzorem
okresach rozpadu połowicznego wyraża się wzorem 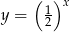 .
.
W przypadku izotopu radu 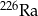 czas połowicznego rozpadu jest równy 1600 lat. Po ilu latach z 1 g
czas połowicznego rozpadu jest równy 1600 lat. Po ilu latach z 1 g 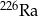 pozostanie nie więcej niż 6,25% masy tego pierwiastka?
pozostanie nie więcej niż 6,25% masy tego pierwiastka?
Firma zatrudniła w tym samym czasie małżeństwo na następujących warunkach: mąż otrzymał za pierwszy przepracowany miesiąc 1200 zł, a żona 1600 zł. Pensja męża będzie wzrastać co miesiąc o 100 zł, a żony o 40 zł.
Trasa rowerowa wokół jeziora ma długość 15 km. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro poruszając się w tym samym kierunku. Średnia prędkość drugiego z nich jest większa od średniej prędkości pierwszego o 5 km/h. Oblicz po jakim czasie dojdzie do ponownego spotkania rowerzystów.
Działkę w kształcie trapezu podzielono przekątnymi na 4 działki. Spośród tych czterech działek wskaż dwie o równych polach. Odpowiedź uzasadnij.
Maszynistka miała do przepisania książkę liczącą 586 stron. Przez pierwsze trzy dni przepisywała po 14 stron dziennie. Następnie postanowiła, że czwartego dnia przepisze o dwie strony więcej niż trzeciego dnia i każdego następnego dnia przepisze o dwie strony więcej niż dnia poprzedniego. W ciągu ilu dni przepisała całą książkę?
Piotrek przez pewien czas rozwiązywał zadania z matematyki. Pierwszego dnia rozwiązał 10 zadań, a każdego kolejnego dnia następnego rozwiązywał o 5 zadań więcej niż w dniu poprzednim. W sumie rozwiązał 220 zadań. Oblicz, przez ile dni rozwiązywał zadania i ile zadań rozwiązał ostatniego dnia.
Dwa samochody odbyły podróż z miejscowości 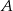 do odległej o 480 km miejscowości
do odległej o 480 km miejscowości  . Drugi z samochodów jechał ze średnią prędkością większą o 20 km/h od średniej prędkości pierwszego samochodu, a czas przejazdu pierwszego samochodu był o 72 minuty dłuższy od czasu przejazdu drugiego samochodu. Oblicz ile czasu zajęła podróż każdemu z samochodów.
. Drugi z samochodów jechał ze średnią prędkością większą o 20 km/h od średniej prędkości pierwszego samochodu, a czas przejazdu pierwszego samochodu był o 72 minuty dłuższy od czasu przejazdu drugiego samochodu. Oblicz ile czasu zajęła podróż każdemu z samochodów.
Miasto  i miasto
i miasto  łączy linia kolejowa długości 210 km. Średnia prędkość pociągu pospiesznego na tej trasie jest o 24 km/h większa od średniej prędkości pociągu osobowego. Pociąg pospieszny pokonuje tę trasę o 1 godzinę krócej niż pociąg osobowy. Oblicz czas pokonania tej drogi przez pociąg pospieszny.
łączy linia kolejowa długości 210 km. Średnia prędkość pociągu pospiesznego na tej trasie jest o 24 km/h większa od średniej prędkości pociągu osobowego. Pociąg pospieszny pokonuje tę trasę o 1 godzinę krócej niż pociąg osobowy. Oblicz czas pokonania tej drogi przez pociąg pospieszny.
Dwóch turystów przebyło tę samą trasę o długości 84 km, przy czym każdy z nich przechodził dziennie tę samą liczbę kilometrów. Pokonanie tej trasy zajęło drugiemu turyście o 3 dni dłużej niż pierwszemu, a pierwszy turysta przechodził dziennie o 9 km więcej od drugiego. Oblicz, ile kilometrów dziennie przechodził każdy z turystów.
Dwa samochody odbyły podróż z miejscowości  do odległej o 252 km miejscowości
do odległej o 252 km miejscowości 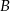 . Średnia prędkość samochodu osobowego na tej trasie była o 24 km/h większa od średniej prędkości samochodu ciężarowego. Oblicz ile czasu zajęła podróż samochodowi osobowemu jeżeli pokonał on tę trasę w czasie o 72 minuty krótszym niż samochód ciężarowy.
. Średnia prędkość samochodu osobowego na tej trasie była o 24 km/h większa od średniej prędkości samochodu ciężarowego. Oblicz ile czasu zajęła podróż samochodowi osobowemu jeżeli pokonał on tę trasę w czasie o 72 minuty krótszym niż samochód ciężarowy.
Wyznacz wszystkie liczby trzycyfrowe, w których cyfra setek jest o 3 większa od cyfry dziesiątek i 2 razy większa od cyfry jedności.
Masa 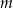 leku
leku 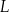 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
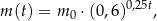
gdzie:
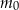 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 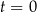 dawki leku,
dawki leku,
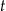 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 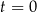 zażycia leku.
zażycia leku.
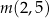 ,
, 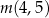 ,
, 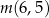 w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu.
w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu. Masa 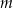 leku
leku 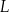 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
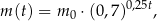
gdzie:
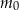 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 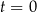 dawki leku,
dawki leku,
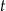 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 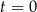 zażycia leku.
zażycia leku.
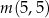 ,
, 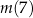 ,
, 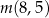 w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu.
w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu. Firma 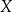 wytwarza pewien produkt
wytwarza pewien produkt 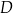 . Badania rynku pokazały, że związek między ilością
. Badania rynku pokazały, że związek między ilością 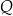 produktu
produktu 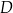 , jaką firma jest w stanie zbyć na rynku, a ceną
, jaką firma jest w stanie zbyć na rynku, a ceną 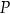 produktu jest następujący:
produktu jest następujący:
![P(Q ) = 90 − 0,1Q , dla Q ∈ [0 ,900],](https://img.zadania.info/zad/8691373/HzadT5x.png)
gdzie 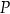 jest ceną za jednostkę produktu w złotych, a
jest ceną za jednostkę produktu w złotych, a 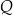 – ilością produktu w tys. sztuk.
– ilością produktu w tys. sztuk.
Koszty 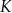 wytworzenia produktu
wytworzenia produktu 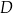 zależą od ilości
zależą od ilości 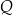 wytwarzanego produktu następująco:
wytwarzanego produktu następująco:
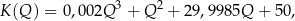
gdzie 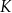 jest kosztem produkcji w tys. zł. Oblicz, przy jakiej wielkości produkcji firma
jest kosztem produkcji w tys. zł. Oblicz, przy jakiej wielkości produkcji firma 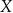 osiąga największy dochód. Wynik podaj zaokrąglony z dokładnością do 100 sztuk.
osiąga największy dochód. Wynik podaj zaokrąglony z dokładnością do 100 sztuk.
Liczbę dodatnią  przedstaw w postaci sumy dwóch takich składników, aby suma ich kwadratów była najmniejsza.
przedstaw w postaci sumy dwóch takich składników, aby suma ich kwadratów była najmniejsza.
Łódź musi płynąć 60 km w dół rzeki, a następnie 10 km w górę rzeki. Prędkość prądu rzeki wynosi 5 km/godz. Jaka powinna być prędkość własna łodzi, aby cała podróż nie trwała dłużej niż 10 godzin?
Koparka, pogłębiająca rów melioracyjny, usypała kopiec w kształcie stożka. Tworząca tego stożka jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 1,5. Przyjmując 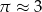 , obliczono, że obwód podstawy kopca jest równy około 12 m. Oblicz, ile kursów będzie musiała wykonać ciężarówka, aby wywieźć wykopany piasek, jeżeli jednorazowo może zabrać
, obliczono, że obwód podstawy kopca jest równy około 12 m. Oblicz, ile kursów będzie musiała wykonać ciężarówka, aby wywieźć wykopany piasek, jeżeli jednorazowo może zabrać 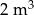 piasku. Przyjmij również, że
piasku. Przyjmij również, że 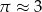 .
.
Jeden z pracowników pewnej firmy otrzymuje stałą pensję miesięczną za 168 przepracowanych godzin oraz dodatkowe wynagrodzenie za nadgodziny. Stawka za godzinę nadliczbową jest o 50% większa niż stawka za godzinę etatową. W styczniu pracownik ten miał 8 nadgodzin i otrzymał razem 2700 zł.
Zmieszano 1 kg solanki o zawartości 18% soli i 2 kg solanki o zawartości 15% soli. Ile procent soli zawiera ta mieszanina?
Zmieszano 2 kg solanki o zawartości 12% soli i 1 kg solanki o zawartości 18% soli. Ile procent soli zawiera ta mieszanina?
Szklankę octu o stężeniu 10% zmieszano z trzema szklankami octu sześcioprocentowego. Jakie jest stężenie otrzymanej mieszanki?
