Sprzedawca kupuje miesięcznie w hurtowni laptopy, płacąc 1200 zł za sztukę. W chwili obecnej sprzedaje 20 laptopów miesięcznie w cenie 1400 zł za sztukę, oraz oszacował, że każda kolejna obniżka ceny o 10 zł zwiększa o 2 liczbę sprzedanych laptopów. Jaką powinien ustalić cenę laptopa, aby jego zysk był największy? Ile jest równy ten maksymalny miesięczny zysk?
/Szkoła średnia/Zadania z treścią
Sprzedawca kupuje miesięcznie w hurtowni monitory, płacąc 1920 zł za sztukę. W chwili obecnej sprzedaje 20 monitorów miesięcznie w cenie 2240 zł za sztukę, oraz oszacował, że każda kolejna obniżka ceny o 16 zł zwiększa o 2 liczbę sprzedanych monitorów. Jaką powinien ustalić cenę monitora, aby jego zysk był największy? Ile jest równy ten maksymalny miesięczny zysk?
Przystań jachtowa dysponuje 80 miejscami w hangarze. Opłata za zimowanie jednego jachtu wynosi 470 zł. Przystań udziela specjalnej zniżki firmom zimującym więcej niż 44 jachty. Wówczas opłata za każdy jacht zimowany przez firmę jest niższa o 5 zł pomnożone przez liczbę jachtów powyżej 44. Przy jakiej liczbie zimowanych jachtów przez jedną firmę (powyżej 44) przystań osiąga maksymalny możliwy przychód?
Wyznacz sumę wszystkich liczb naturalnych trzycyfrowych, które przy dzieleniu przez 4 dają resztę 3.
Sprzedawcy lizaków udało się korzystnie zakupić pewną ilość tych słodyczy. Zapłacił za nie w sumie 243 korony. Po pewnym czasie zdecydował się sprzedać lizaki. Sprzedał je wszystkie po 18 koron za sztukę. Dochód ze sprzedaży równy był sumie, za jaką zakupił na początku 6 lizaków. Ile lizaków sprzedawca nabył na początku?
Stasiu wybrał się na spacer po lesie. Na wykresie przedstawiono przebytą przez niego drogę w zależności od czasu.
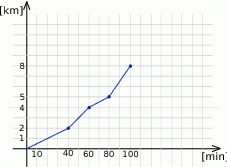
- Oblicz z jaką średnią prędkością poruszał się w trakcie spaceru. Wynik podaj w kilometrach na godzinę.
- W której minucie spaceru przebył dokładnie połowę drogi?
- Z jaką największą, i z jaką najmniejszą prędkością się poruszał? Wynik podaj w kilometrach na godzinę.
W kartonach rozmieszczono 2800 metalowych puszek w ten sposób, że w każdym kartonie znajduje się ta sama liczba puszek. Gdyby do każdego kartonu włożyć o 15 puszek mniej, to należałoby użyć o 60 kartonów więcej. W ilu kartonach rozmieszczono puszki?
Dwie partie konserw rybnych, liczące po 1440 konserwy każda, zapakowano w kartony. Każdą z partii zapakowano w ten sposób, że w każdym kartonie znalazła się ta sama liczba konserw, przy czym w przypadku drugiej partii liczbę kartonów zmniejszono o 2 i w kartonach umieszczono o 10 konserw więcej, niż w przypadku kartonów pierwszej partii. Do ilu łącznie kartonów zapakowano te dwie partie konserw?
Na szczyt góry wożą narciarzy 3 wyciągi: gondolowy, krzesełkowy i orczykowy. Gondolowy wwozi grupę 1200 narciarzy o 2 godziny krócej niż krzesełkowy i 3 razy szybciej niż orczykowy. Jeżeli wszystkie wyciągi są czynne to grupa 1200 narciarzy wjeżdża na szczyt w ciągu 2 godzin. Ilu narciarzy wjeżdża na szczyt w ciągu 1 godziny każdym wyciągiem?
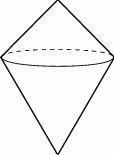
Boja ma kształt dwóch stożków połączonych podstawami, przy czym kąty rozwarcia tych stożków są równe 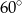 i
i 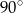 , a odległość ich wierzchołków jest równa
, a odległość ich wierzchołków jest równa 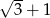 . Oblicz pole powierzchni tej boi.
. Oblicz pole powierzchni tej boi.
Statek wycieczkowy, płynąc z prądem rzeki, pokonuje trasę z miasta 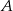 do miasta
do miasta 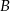 w ciągu dwóch godzin, natomiast z powrotem płynie o pół godziny dłużej. Ile czasu będzie płynąć tratwa z miasta
w ciągu dwóch godzin, natomiast z powrotem płynie o pół godziny dłużej. Ile czasu będzie płynąć tratwa z miasta 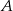 do miasta
do miasta 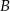 ?
?
Liczbę 49 rozłóż na dwa dodatnie składniki tak, aby ich iloczyn był największy. Podaj wartość iloczynu.
Pan Alojzy postanowił co miesiąc odkładać pewną sumę pieniędzy. W pierwszym miesiącu odłożył 100 zł, a w każdym następnym odkładał o 5% więcej niż w poprzednim. Razem z panem Alojzym oszczędzanie rozpoczęła jego małżonka, przy czym odłożyła ona w pierwszym miesiącu 110 zł, a w każdym następnym odkładała o 3% więcej, niż w poprzednim. Oblicz, która z tych dwóch osób zaoszczędzi więcej pieniędzy po roku oszczędzania.
Droga z miasta 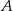 do miasta
do miasta 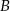 ma długość 474 km. Samochód jadący z miasta
ma długość 474 km. Samochód jadący z miasta 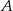 do miasta
do miasta 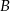 wyrusza godzinę później niż samochód z miasta
wyrusza godzinę później niż samochód z miasta 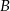 do miasta
do miasta 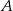 . Samochody te spotykają się w odległości 300 km od miasta
. Samochody te spotykają się w odległości 300 km od miasta 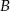 . Średnia prędkość samochodu, który wyjechał z miasta
. Średnia prędkość samochodu, który wyjechał z miasta 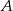 , liczona od chwili wyjazdu z
, liczona od chwili wyjazdu z 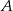 do momentu spotkania, była o 17 km/h mniejsza od średniej prędkości drugiego samochodu liczonej od chwili wyjazdu z
do momentu spotkania, była o 17 km/h mniejsza od średniej prędkości drugiego samochodu liczonej od chwili wyjazdu z 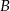 do chwili spotkania. Oblicz średnią prędkość każdego samochodu do chwili spotkania.
do chwili spotkania. Oblicz średnią prędkość każdego samochodu do chwili spotkania.
Z miast 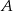 i
i 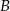 odległych o 330 km wyjechały naprzeciwko siebie dwa samochody. Samochód jadący z miasta
odległych o 330 km wyjechały naprzeciwko siebie dwa samochody. Samochód jadący z miasta 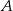 wyjechał 20 minut wcześniej i jechał z prędkością o 9 km/h mniejszą niż samochód jadący z miasta
wyjechał 20 minut wcześniej i jechał z prędkością o 9 km/h mniejszą niż samochód jadący z miasta 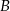 . Samochody te minęły się w odległości 168 km licząc od miasta
. Samochody te minęły się w odległości 168 km licząc od miasta 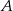 . Oblicz średnią prędkość każdego z samochodów.
. Oblicz średnią prędkość każdego z samochodów.
Linia kolejowa między miastami 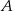 i
i 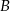 ma długość 711 km. Pociąg jadący z miasta
ma długość 711 km. Pociąg jadący z miasta 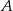 do miasta
do miasta 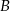 wyrusza 45 minut później niż pociąg jadący z miasta
wyrusza 45 minut później niż pociąg jadący z miasta 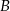 do
do 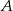 . Pociągi te spotykają się w odległości 450 km od miasta
. Pociągi te spotykają się w odległości 450 km od miasta 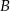 . Średnia prędkość pociągu, który wyjechał z miasta
. Średnia prędkość pociągu, który wyjechał z miasta 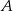 , liczona od chwili wyjazdu z
, liczona od chwili wyjazdu z 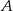 do momentu spotkania, była o 34 km/h mniejsza od średniej prędkości drugiego pociągu liczonej od chwili wyjazdu z miasta
do momentu spotkania, była o 34 km/h mniejsza od średniej prędkości drugiego pociągu liczonej od chwili wyjazdu z miasta 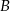 do chwili spotkania. Oblicz średnią prędkość każdego z pociągów w chwili spotkania.
do chwili spotkania. Oblicz średnią prędkość każdego z pociągów w chwili spotkania.
Suma kwadratów trzech kolejnych liczb naturalnych wynosi 149. Wyznacz te liczby.
W karczmie jest 30 litrowa beczka wina napełniona do pełna. Winiarz zaczerpnął 1 litr wina i dolał do beczki 1 litr wody. Postąpił tak 10 razy. Ile czystego wina zostało w beczce.
Dwie szkoły mają prostokątne boiska. Przekątna każdego boiska jest równa 65 m. Boisko w drugiej szkole ma długość o 4 m większą niż boisko w pierwszej szkole, ale szerokość o 8 m mniejszą. Oblicz długość i szerokość każdego z tych boisk.
Z dwóch okrągłych kawałków blachy o średnicy 25 cm wycięto dwa prostokąty w ten sposób, że wierzchołki prostokątów znajdowały się na brzegu kół (patrz rysunek).
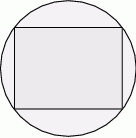
Pierwszy prostokąt miał długość o 4 cm większą niż drugi prostokąt, ale szerokość o 8 cm mniejszą. Oblicz długość i szerokość każdego z prostokątów.
Pomiędzy miastami 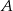 i
i 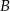 kursuje autobus. Droga między tymi miastami prowadzi przez wzgórze. Autobus jadąc pod górę rozwija prędkość 25 km/h, a z góry 50 km/h. Podróż z
kursuje autobus. Droga między tymi miastami prowadzi przez wzgórze. Autobus jadąc pod górę rozwija prędkość 25 km/h, a z góry 50 km/h. Podróż z 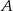 do
do 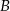 trwa 3,5 h, a z
trwa 3,5 h, a z 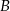 do
do 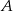 4 h. Jaka jest odległość z
4 h. Jaka jest odległość z 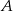 do
do 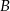 ?
?
Dwa pociągi: towarowy o długości 490 m i osobowy o długości 210 m, jadą naprzeciw siebie po dwóch równoległych torach i spotykają się w miejscu 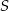 . Mijanie się pociągów trwa 20 s, a czas przejazdu pociągu osobowego przez miejsce
. Mijanie się pociągów trwa 20 s, a czas przejazdu pociągu osobowego przez miejsce 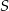 jest o 25 sekund krótszy od czasu przejazdu pociągu towarowego. Oblicz prędkości obu pociągów, zakładając, że poruszają się ruchem jednostajnym.
jest o 25 sekund krótszy od czasu przejazdu pociągu towarowego. Oblicz prędkości obu pociągów, zakładając, że poruszają się ruchem jednostajnym.
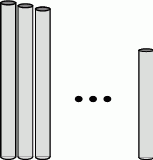
Fragment palisady wokół średniowiecznego grodu składa się z coraz krótszych pionowych bali. Najwyższy z bali ma długość 350 cm, a każdy kolejny jest krótszy o 5 cm. Wiedząc, że całkowita długość wszystkich bali wynosi 50 m oblicz ile jest tych bali i jaka jest długość najkrótszego z nich.
Trzech znajomych: Jacek, Karol i Bogdan pokonało samochodami trasę pomiędzy miastami 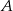 i
i 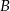 , przy czym Karol wyjechał pół godziny później niż Jacek i pół godziny wcześniej niż Bogdan. Cała trójka dojechała do miasta
, przy czym Karol wyjechał pół godziny później niż Jacek i pół godziny wcześniej niż Bogdan. Cała trójka dojechała do miasta 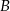 o tej samej godzinie. Średnia prędkość Jacka na całej trasie wyniosła 50 km/h, a Karola 60 km/h. Oblicz jaka była średnia prędkość Bogdana na tej trasie.
o tej samej godzinie. Średnia prędkość Jacka na całej trasie wyniosła 50 km/h, a Karola 60 km/h. Oblicz jaka była średnia prędkość Bogdana na tej trasie.
Do wyznaczenia trzech boków pewnego kąpieliska w kształcie prostokąta należy użyć liny o długości 200 m. Czwarty bok tego kąpieliska będzie pokrywał się z brzegiem plaży, który w tym miejscu jest linią prostą (zobacz rysunek).
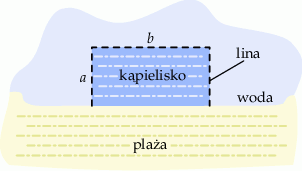
Oblicz wymiary  i
i 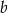 kąpieliska tak, aby jego powierzchnia była największa.
kąpieliska tak, aby jego powierzchnia była największa.
Do wyznaczenia boków pewnego kąpieliska w kształcie prostokąta należy użyć liny o długości 80 m. Część jednego z boków tego kąpieliska będzie pokrywać się z końcem pomostu i na tym odcinku lina nie jest potrzebna (zobacz rysunek). Pomost ma szerokość 4 metrów.
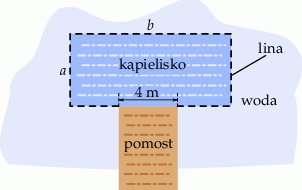
Oblicz wymiary  i
i 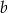 kąpieliska tak, aby jego powierzchnia była największa.
kąpieliska tak, aby jego powierzchnia była największa.
Do wyznaczenia trzech pastwisk na pewnej łące należy użyć ogrodzenia elektrycznego o łącznej długości 960 metrów. Dwa z tych pastwisk mają mieć kwadratowy kształt, a trzecie ma mieć kształt prostokąta, którego jeden z boków jest dwa razy dłuższy od boku pastwiska w kształcie kwadratu (zobacz rysunek).
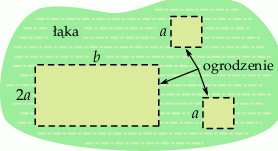
Oblicz wymiary  i
i 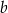 tych pastwisk tak, aby ich łączna powierzchnia była największa możliwa. Oblicz tą największą powierzchnię.
tych pastwisk tak, aby ich łączna powierzchnia była największa możliwa. Oblicz tą największą powierzchnię.
W schronisku dla zwierząt, na płaskiej powierzchni, należy zbudować ogrodzenie z siatki wydzielające trzy identyczne wybiegi o wspólnych ścianach wewnętrznych. Podstawą każdego z tych trzech wybiegów jest prostokąt (jak pokazano na rysunku). Do wykonania tego ogrodzenia należy zużyć 36 metrów bieżących siatki.
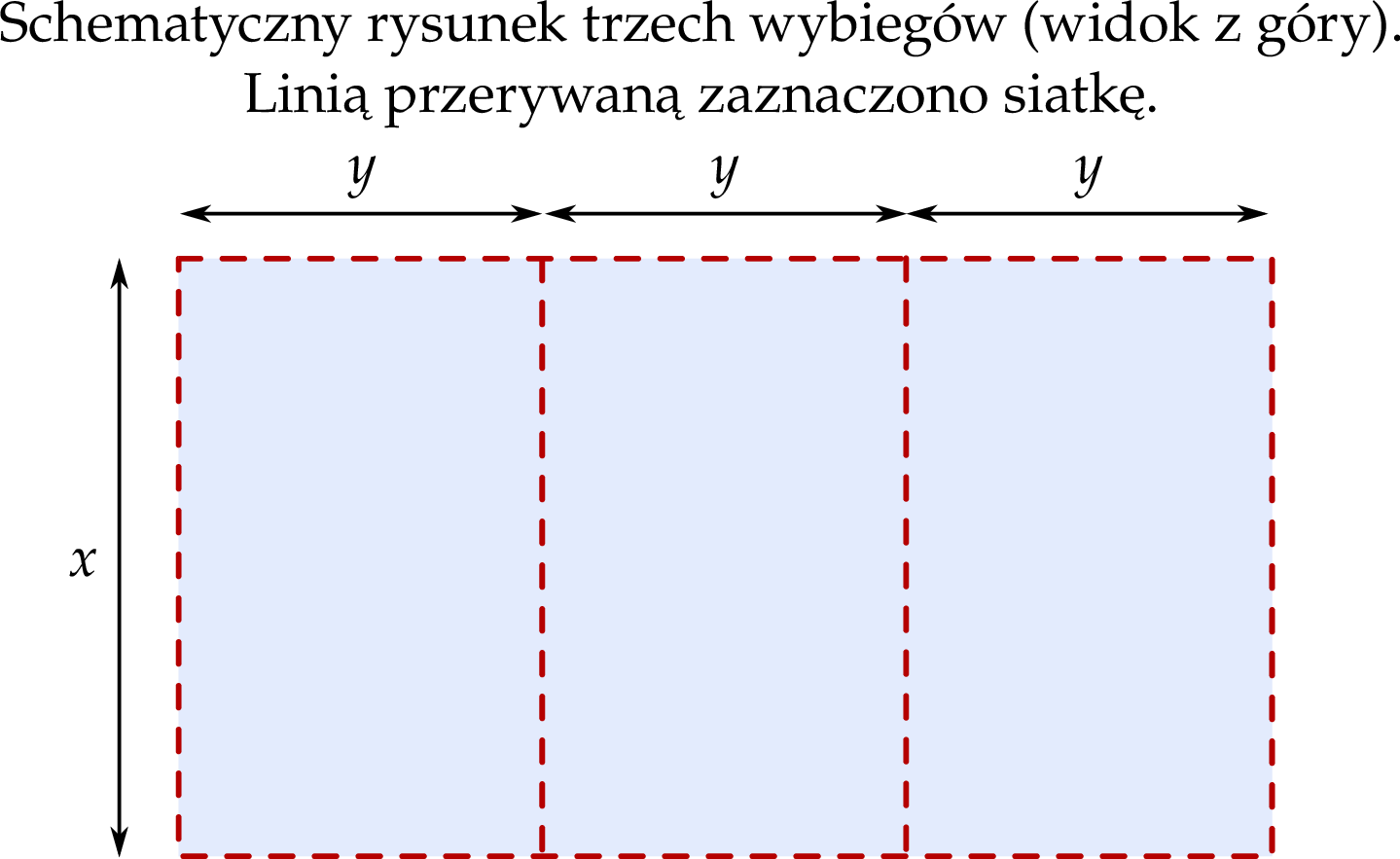
Oblicz wymiary  oraz
oraz 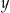 jednego wybiegu, przy których suma pól podstaw tych trzech wybiegów będzie największa. W obliczeniach pomiń szerokość wejścia na każdy z wybiegów.
jednego wybiegu, przy których suma pól podstaw tych trzech wybiegów będzie największa. W obliczeniach pomiń szerokość wejścia na każdy z wybiegów.
Powierzchnia magazynowa będzie się składała z dwóch identycznych prostokątnych działek połączonych wspólnym bokiem. Całość ma być ogrodzona płotem, przy czym obie działki będzie rozdzielał wspólny płot. W ogrodzeniu będą zamontowane dwie bramy wjazdowe, każda o szerokości 10 m (zobacz rysunek poniżej). Łączna długość płotu ogradzającego oraz rozdzielającego obie działki wyniesie 580 metrów, przy czym szerokości obu bram wjazdowych nie wliczają się w długość płotu.
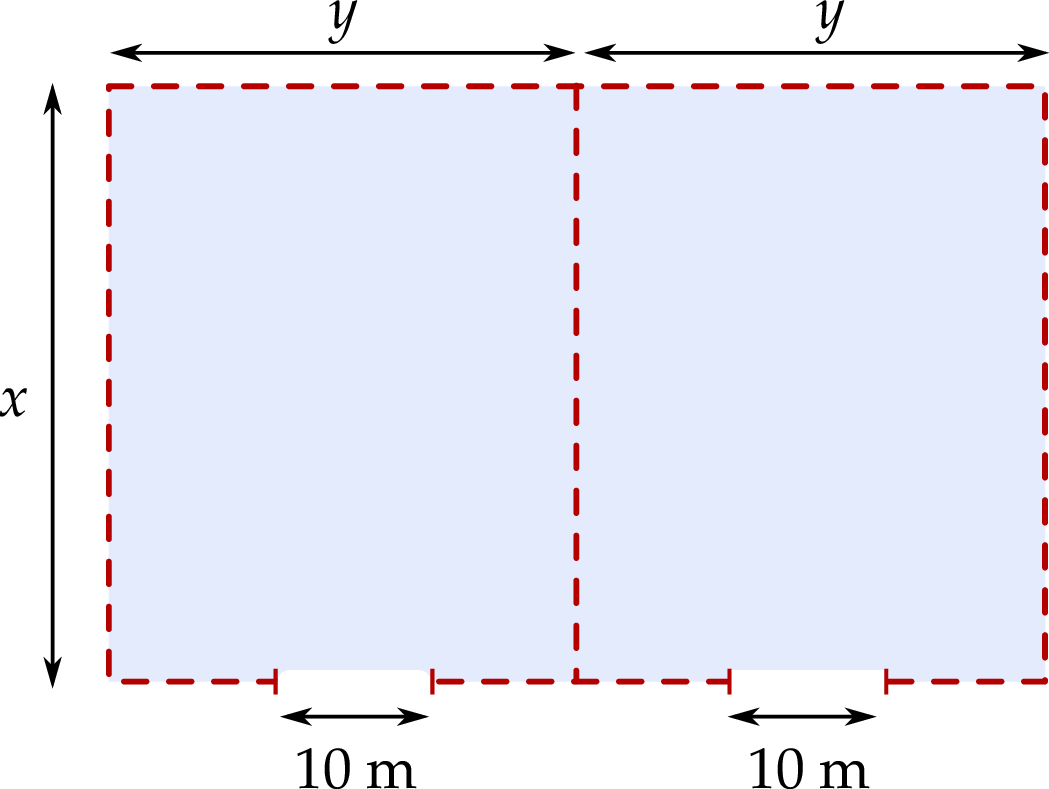
Oblicz wymiary  oraz
oraz 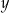 każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
Statek płynący z prędkością własną 25 km/h, przepływa odległość z portu 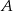 do
do 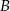 z prądem rzeki w ciągu 40 godzin natomiast drogę powrotną płynąc pod prąd w ciągu 60 godzin. Oblicz średnią prędkość prądu rzeki, oraz odległość między portami
z prądem rzeki w ciągu 40 godzin natomiast drogę powrotną płynąc pod prąd w ciągu 60 godzin. Oblicz średnią prędkość prądu rzeki, oraz odległość między portami 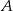 i
i 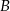 .
.

