Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Zadania z treścią

Wyszukiwanie zadań

Fabryka odzieży w pierwszym roku produkcji wyprodukowała 2000 kurtek i 1000 par spodni. W każdym kolejnym roku produkcję par spodni zwiększano o 400 sztuk, a produkcję kurtek zmniejszano o 20%. Po ilu latach produkcji łączna liczba (od początku działalności fabryki) wyprodukowanych par spodni przekroczy łączną liczbę wyprodukowanych kurtek?

W pewnym nadleśnictwie postanowiono wymienić drzewostan na obszarze 150 hektarów. W pierwszym roku zaplanowano wymianę na obszarze 3 hektarów i ustalono normę, według której w każdym następnym roku będzie się dokonywać wymiany na obszarze o 1 hektar większym niż w roku poprzednim.

  • Oblicz, ile lat będzie trwać wymiana drzewostanu na zaplanowanym obszarze.
  • Oblicz, o ile należałoby zwiększyć normę wymiany drzewostanu, aby skrócić cały proces o 5 lat.
  • W obu przypadkach oblicz liczbę hektarów, na których dokonana zostanie wymiana w ostatnim roku.

Taryfa dzienna zużycia energii na godzinę wynosi 20 gr, a nocna 12 gr. Ile godzin trwa taryfa nocna, a ile dzienna, jeśli wiadomo, że średnia to 18gr?

Motocyklista drogę z miasta 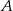A do miasta 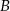B pokonał ze średnią prędkością 84 km/h. Pokonanie drogi powrotnej zajęło mu o godzinę dłużej, a średnia prędkość wyniosła 56 km/h. Oblicz odległość między miastami 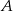A i B .

Ukryj Podobne zadania

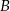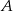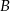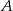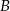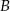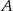Miejscowości A i B są połączone linią kolejową. Pociąg przebywa trasę z A do B ze średnią prędkością 80 km/h. W drodze powrotnej średnia prędkość pociągu jest większa o 20 km/h i dzięki temu pociąg pokonuje trasę od B do A w czasie o godzinę krótszym. Jaka jest długość linii kolejowej między miejscowościami 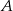A i B ?

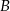Rozłożono 100 cukierków na 5 talerzach.
Na 1 i 2 talerzu znalazły się łącznie 52 cukierki,
na 2 i 3 talerzu 43 cukierki,
na 3 i 4 talerzu 34 cukierki,
na 4 i 5 talerzu 30 cukierków.
Ile cukierków znajdowało się na każdym talerzu?

Marta spłacała kredyt wysokości 5100 zł w ciągu jednego roku, tj. w 12 ratach. Każda kolejna rata była niższa od poprzedniej o 50 zł. Ile wynosiła pierwsza oraz ostatnia rata spłaty?

Ukryj Podobne zadania

Pan Stanisław spłacił pożyczkę w wysokości 8910 zł w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 30 zł. Oblicz kwotę pierwszej raty.

Pani Dagmara spłaciła pożyczkę w wysokości 8800 zł w szesnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 40 zł. Oblicz kwotę pierwszej raty.

Czy okrągła serweta o średnicy 1,4 m przykryje kwadratowy stół o boku 1 m?

Klient zaciągnął w banku pożyczkę w wysokości 7200 zł. Spłatę rozłożył na 10 rat, z których każda następna jest mniejsza od poprzedniej o 60 zł. Oblicz sumę pierwszych pięciu rat.

W skarbcu królewskim było 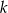k monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę 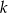k , dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości 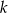k oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.

Na diagramie przedstawiono wyniki sprawdzianu z matematyki w klasie 1a.

PIC

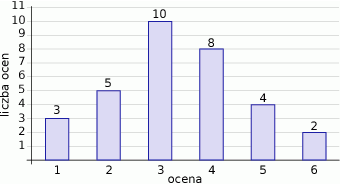
  • Jaki procent uczniów tej klasy otrzymał ze sprawdzianu ocenę co najmniej dostateczny?
  • O ile procent więcej uczniów otrzymało ocenę dostateczny niż ocenę celujący?
Ukryj Podobne zadania

Na diagramie przedstawiono wyniki sprawdzianu z matematyki w klasie 1c.

PIC

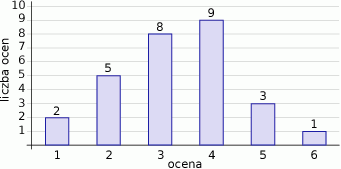
  • Jaki procent uczniów tej klasy otrzymał ze sprawdzianu ocenę co najmniej dostateczny?
  • O ile procent więcej uczniów otrzymało ocenę dostateczny niż ocenę niedostateczny?

Czterej koledzy wybrali się na wakacje nad jezioro odległe o 80 km od miejsca zamieszkania. Po przyjeździe najmłodszy z nich zobaczył, że na mapie w skali 1:400 000 powierzchnia jeziora wynosi 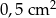0,5 cm 2 . Oblicz rzeczywistą powierzchnię tego jeziora.

Ukryj Podobne zadania

Na mapie o skali 1:50 000 las ma powierzchnię 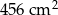2 456 cm . Jaką rzeczywistą powierzchnię ma las?

Ze Szczecina do Częstochowy wybrały się dwie pielgrzymki: piesza i rowerowa. Pielgrzymka piesza wyruszyła pierwsza, pokonując każdego dnia 26 km. Po 8 dniach wyruszyła (z tego samego miejsca, tą samą trasą) pielgrzymka rowerowa, pokonując pierwszego dnia 54 km, a każdego następnego dnia o 2 kilometry mniej niż dnia poprzedniego. Pielgrzymki spotkały się dopiero u stóp Jasnej Góry. W którym dniu podróży i w jakiej odległości od miejsca wyjazdu pielgrzymka rowerowa dogoniła pielgrzymkę pieszą?

Właściciel sklepu muzycznego „Tra-la-la” kupuje w hurtowni płyty zespołu „Emotion” po 30 zł za sztukę i sprzedaje 56 sztuk miesięcznie, po 50 zł za sztukę. Badania rynku wykazały, że każda obniżka ceny płyty o 1 zł, zwiększy liczbę sprzedanych płyt o 4 sztuki (miesięcznie).

  • Wyznacz wzór funkcji miesięcznego zysku właściciela sklepu „Tra-la-la” w zależności od obniżki ceny płyty zespołu „Emotion” (w pełnych złotych). Podaj dziedzinę tej funkcji.
  • Jaką cenę płyty powinien ustalić sprzedawca, aby miesięczny zysk z jej sprzedaży był największy? Oblicz miesięczny największy zysk właściciela sklepu ze sprzedaży płyty „Emotion”.
Ukryj Podobne zadania

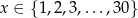Właściciel sklepu kupuje zegarki płacąc producentowi 180 zł za sztukę. Następnie sprzedaje miesięcznie 30 sztuk takich zegarków po 230 zł. Sprzedawca oszacował, że każda obniżka ceny zegarka o złotówkę zwiększy liczbę sprzedanych zegarków o trzy sztuki. Niech x oznacza liczbę obniżek o 1 zł, gdzie x ∈ {1,2,3,...,30} .

  • Wyznacz wzór funkcji miesięcznego zysku właściciela sklepu w zależności od x .
  • Jaką cenę zegarka powinien ustalić właściciel sklepu, aby jego miesięczny zysk był największy? Ile będzie równy ten największy miesięczny zysk?

Parking wyłożono płytami betonowymi w kształcie prostokątów. Gdyby ten sam parking wyłożyć prostokątnymi płytami o powierzchni większej o 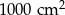10 00 cm 2 to liczba użytych płyt zmniejszyłaby się o 8. Gdyby natomiast użyć płyt o powierzchni mniejszej o 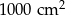1000 cm 2 , to liczba użytych płyt zwiększyłaby się o 12. Oblicz pole powierzchni parkingu.

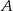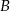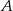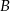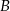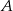Z dwóch miejscowości A i B wyruszyły naprzeciw siebie ruchem jednostajnym dwa pociągi. Po upływie trzech godzin minęły się. Pierwszy pociąg przejechał trasę z A do B w ciągu 7,5 godziny. W jakim czasie drogę z B do A przejechał drugi pociąg?

Suma cyfr liczby dwucyfrowej n jest mniejsza od 12. Różnica tej liczby i liczby dwucyfrowej otrzymanej po przestawieniu jej cyfr jest równa 36. Wyznacz możliwe wartości liczby n .

Różnica kwadratów dwóch kolejnych liczb naturalnych wynosi 13. Wyznacz te liczby.

Ukryj Podobne zadania

Różnica kwadratów dwóch kolejnych liczb naturalnych wynosi 17. Wyznacz te liczby.

Na początku 2002 roku zasoby węgla kamiennego w Polsce szacowane były na 64 mld ton. W 2002 roku w Polsce wydobyto 103,7 mln ton wegla. Jaki procent zasobów węgla kamiennego w naszym kraju uległby wyczerpaniu do końca 2101 roku, gdyby każdego roku wydobycie węgla wzrastało o 0,4 mln ton? Wynik zaokrąglij do pierwszego miejsca po przecinku.

Turysta zwiedzał zamek stojący na wzgórzu. Droga łącząca parking z zamkiem ma długość 2,1 km. Łączny czas wędrówki turysty z parkingu do zamku i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 1 godzinę i 4 minuty. Oblicz, z jaką średnią prędkością turysta wchodził na wzgórze, jeżeli prędkość ta była o 1 km/h mniejsza od średniej prędkości, z jaką schodził ze wzgórza.

Ukryj Podobne zadania

Turysta zwiedzał zabytkowy młyn stojący w dolinie rzeki. Droga łącząca parking z młynem ma długość 1,8 km. Łączny czas wędrówki turysty z parkingu do młyna i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 54 minuty. Oblicz, z jaką średnią prędkością turysta schodził w dolinę, jeżeli prędkość ta była o 0,9 km/h większa od średniej prędkości, z jaką wracał na parking.

Wazon ma kształt sześcianu, w którym wydrążony jest walec w taki sposób, że styczne górnej podstawy walca, równoległe do odpowiednich krawędzi górnej podstawy sześcianu, są odległe o 1 cm od tych krawędzi; natomiast odległość między dolną podstawą walca, a dolną podstawą sześcianu (grubość dna) jest równa 2 cm.

PIC

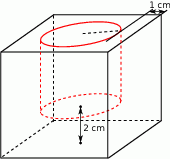
Wiedząc, że stosunek objętości walca do objętości sześcianu jest równy 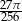272π56 , oblicz

  • długość krawędzi sześcianu;
  • objętość walca;
  • do jakiej wysokości wazonu (licząc od dolnej podstawy walca) będzie sięgać poziom wody, jeśli wlejemy do wazonu 125 ml wody. Wynik podaj z dokładnością do 1 mm.
Strona 2 z 17