Zadania z treścią/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Zadania z treścią

Uzasadnij, że jeżeli jest dowolną cyfrą, to mnożąc liczbę 37037 przez liczbę 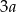otrzymamy liczbę, której wszystkie cyfry są równe .

Suma dwóch liczb, ich iloczyn i różnica ich kwadratów są równe. Wyznacz te liczby.

Czy można z prostokątnego kawałka materiału o wymiarach 117 cm na 80 cm wyciąć trzy okrągłe serwetki: dwie o promieniu 20 cm i jedną o promieniu 40 cm?

Suma stu kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 2 wynosi 30950. Wyznacz najmniejszą i największą z tych liczb.

Różnica dwóch liczb naturalnych dodatnich mniejszych od 160 jest równa 119, a ich największy wspólny dzielnik jest równy 17. Wyznacz te liczby.

Ukryj Podobne zadania

Różnica dwóch liczb naturalnych dodatnich mniejszych od 130 jest równa 98, a ich największy wspólny dzielnik jest równy 14. Wyznacz te liczby.

Z okrągłego skrawka materiału wycięto trójkąt równoboczny jak na rysunku poniżej.

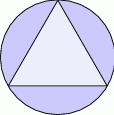
Oblicz jaki procent pola okrągłego skrawka stanowi pole wyciętego trójkąta. Przyjmując, że 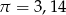π = 3 ,1 4 , wynik podaj z dokładnością do 1%.

Suma sześcianów trzech kolejnych liczb całkowitych wynosi -36. Wyznacz te liczby.

Oblicz ile wynosi suma wszystkich liczb naturalnych 3-cyfrowych.

Samochód 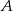, jadący pod górę, w pierwszej sekundzie pokonał 25 m, a w każdej następnej o pół metra mniej niż w poprzedniej. W tym samym momencie, gdy 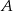rozpoczął podjazd, zjazd z góry rozpoczął samochód 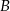, będący w odległości 360 m od 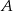. Samochód 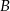w pierwszej sekundzie przebył drogę 9 m, a w każdej następnej o 2 m więcej niż w poprzedniej. Jaką odległość pokonał samochód 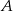do chwili minięcia z samochodem ?

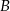Dwóch korektorów, pracując razem, jest w stanie dokonać poprawek w tekście w czasie 8 godzin. Jeżeli każdy z nich wykonywałby tę pracę sam, to pierwszy, bardziej doświadczony korektor zakończyłby ją o 12 godzin wcześniej niż drugi. W ciągu ilu godzin każdy z korektorów wykonałby tę pracę samodzielnie?

Ukryj Podobne zadania

Pierwsza pompa napełnia zbiornik w czasie o 15 godzin krótszym niż druga pompa. Jeżeli obie pompy pracują jednocześnie, to zbiornik zostaje napełniony w czasie 10 godzin. Ile godzin potrzeba na napełnienie zbiornika przy pomocy każdej z pomp?

Basen można napełnić dwoma kranami w ciągu 6 godzin. Pierwszy kran napełnia basen w czasie o 5 godzin krótszym niż drugi. W ciągu ilu godzin, każdy kran oddzielnie napełni basen.

Basen można napełnić dwoma kranami w ciągu 3 godzin. Pierwszy kran napełnia basen w czasie o 8 godzin krótszym niż drugi. W ciągu ilu godzin, każdy kran oddzielnie napełni basen.

Basen można napełnić, otwierając zawór nr 1, a opróżnić, odkręcając zawór nr 2. Jeśli otworzony jest tylko jeden zawór, całkowite napełnienie basenu trwa o godzinę krócej niż jego opróżnienie. Gdy równocześnie odkręcono obydwa zawory, basen napełnił się w ciągu 12 godzin. W ciągu ilu godzin napełni się basen, jeżeli zawór nr 2 będzie zamknięty?

Przedsiębiorstwo oszacowało, że koszt uruchomienia produkcji lamp nowego typu wyniesie 15 600 zł, a koszt pojedynczej lampy wyniesie 80 zł. Niech oznacza liczbę wyprodukowanych lamp.

Wyraź całkowity koszt produkcji lamp jako funkcję argumentu .
Wyraź całkowity zysk jako funkcję argumentu , jeżeli przedsiębiorstwo sprzedaje hurtowniom lampy po 100 zł za sztukę.
Ile sztuk sprzedanych lamp zwróci koszty uruchomienia ich produkcji.

Jaka jest wysokość budynku rzucającego cień długości 19 m w momencie, gdy promienie słoneczne padają pod kątem 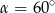α = 60∘ . Wynik podaj z dokładnością do 10 cm.

Codzienna trasa listonosza ma kształt trójkąta równobocznego, którego wierzchołki stanowią bloki 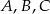A ,B,C . Z bloku 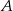do bloku 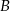listonosz idzie z prędkością 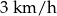3 km/h . Z bloku 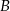do bloku 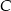idzie z prędkością dwukrotnie większą. Średnia prędkość na całej trasie jest równa 4 km/h. Oblicz, z jaką średnią prędkością listonosz porusza się od bloku 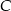do bloku .

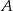Ze środka górnej ściany sześcianu wypuszczono promień świetlny, który odbija się od ścian sześcianu zgodnie z zasadą „kąt padania jest równy kątowi odbicia”. Promień porusza się w płaszczyźnie prostopadłej do jednej ze ścian sześcianu oraz został wypuszczony pod kątem 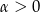α > 0 wględem prostej prostopadłej do górnej ściany sześcianu i przechodzącej przez jej środek. Dla jakich wartości 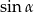sin α promień odbije się od bocznej ściany sześcianu, a potem traﬁ w dolną ścianę sześcianu?

W dwóch hotelach wybudowano prostokątne baseny. Basen w pierwszym hotelu ma powierzchnię 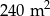24 0 m 2 . Basen w drugim hotelu ma powierzchnię 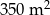35 0 m 2 oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.

Ukryj Podobne zadania

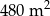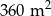Dwie prostokątne działki ogrodnicze mają odpowiednio pola powierzchni 48 0 m 2 i 360 m 2 . Druga z działek jest o 2 metry węższa i o 4 metry krótsza od pierwszej działki. Oblicz, jakie wymiary mogą mieć działki. Podaj wszystkie możliwe odpowiedzi.

Dwie szkoły wybudowały boiska do piłki nożnej. Powierzchnia pierwszego ma 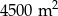45 00 m 2 . Drugie boisko jest o 10 metrów szersze oraz 20 metrów dłuższe od pierwszego i ma powierzchnię 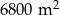6800 m 2 . Podaj wymiary obu boisk szkolnych. Uwzględnij wymaganie, że boisko piłkarskie musi mieć kształt prostokąta, ale nie może być kwadratem. Długość boiska do piłki nożnej nie może przekraczać 120 metrów ani być mniejsza niż 70 metrów. Musi też być w każdym przypadku dłuższa od szerokości boiska, która ma mieścić się w przedziale od 45 m do 90 m.

W dwóch szkołach wybudowano prostokątne baseny. W pierwszej z nich powierzchnia basenu wynosi 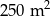25 0 m 2 , w drugiej zaś jest o 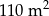110 m 2 większa, a boki prostokąta odpowiednio dłuższe o 2 m na szerokości i o 5 m na długości basenu. Oblicz wymiary basenów w obu szkołach.

Dane są dwie prostokątne działki. Działka pierwsza ma powierzchnię równą 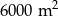60 00 m 2 . Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o 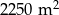2250 m 2 . Oblicz wymiary pierwszej działki.

W chwili początkowej 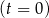(t = 0) masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 19% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej 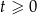t ≥ 0 funkcja 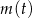m (t) określa masę substancji w gramach po 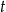pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji 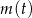m (t) . Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 1,5 grama.

Ukryj Podobne zadania

W chwili początkowej 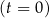(t = 0) masa substancji jest równa 12 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 21% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej 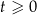t ≥ 0 funkcja 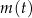m (t) określa masę substancji w gramach po 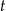pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji 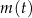m (t) . Oblicz, przez ile pełnych dób masa tej substancji będzie przekraczać 3 gramy.

Do sklepu rowerowego dostarczono 30 rowerów dziecięcych, wśród których były dwa rodzaje rowerów: dwukołowe i trójkołowe. W sumie w dostarczonych rowerach było 67 kół. Ile rowerów dwukołowych i ile rowerów trójkołowych dostarczono do sklepu? Zapisz obliczenia.

Wśród 360 uczniów pewnej szkoły przeprowadzono ankietę, w której jedno z pytań brzmiało czy oglądałeś/oglądałaś wczoraj telewizję. Odpowiedzi na to pytanie są przedstawione na wykresach poniżej.

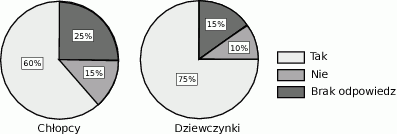
Wiedząc, że dziewczęta stanowią 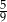ankietowanych osób odpowiedz na pytania.

Ile sposród ankietowanych osób nie odpowiedziało na zadane pytanie?
Jaki procent ankietowanych osób oglądało wczoraj telewizję? Wynik podaj z dokładnością do 1%.
Jaki procent chłopców, spośród tych, którzy udzielili odpowiedzi na pytanie, nie oglądało wczoraj telewizji?

Droga z miejscowości 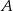do miejscowości 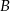ma długość 26 km. Motocyklista przebył tę drogę w czasie o 1,5 h krótszym niż rowerzysta, który jechał z prędkością o 39 km/h mniejszą. Oblicz, z jaką prędkością jechał motocyklista, a z jaką rowerzysta.

Ukryj Podobne zadania

Trasę etapu wyścigu kolarskiego o długości 150 km pan Nowak pokonał w czasie o 1 godzinę i 50 minut krótszym niż jego kolega z drużyny, pan Kowalski. Średnia wartość prędkości, z jaką pan Nowak jechał na tym etapie, była o 11 km/h większa od średniej wartości prędkości pana Kowalskiego na tej trasie. Oblicz średnie wartości prędkości, z jakimi przejechali całą trasę obaj zawodnicy.

Dwa miasta łączy linia kolejowa o długości 336 kilometrów. Pierwszy pociąg przebył tę trasę w czasie o 40 minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o 9 km/h większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.

Dwa miasta łączy droga o długości 448 kilometrów. Samochód 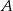przebył tę trasę w czasie o 40 minut krótszym niż samochód 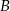. Średnia prędkość samochodu 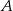na tej trasie była o 12 km/h większa od średniej prędkości samochodu 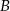. Oblicz średnią prędkość każdego z tych samochodów na tej trasie.

Miasta 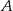i 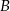są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości:
– prędkości, z jaką pani Danuta jechała z A do B.
– prędkości, z jaką pani Lidia jechała z A do B.

Pociąg towarowy pokonał trasę długości 208 km. Gdyby średnia prędkość pociągu była większa o 13 km/h to tę samą trasę pociąg pokonałby w czasie o 48 minut krótszym. Oblicz średnią prędkość z jaką pociąg pokonał tę trasę.

Oblicz 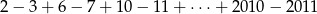2 − 3 + 6 − 7 + 10 − 11 + ⋅⋅⋅ + 2010 − 2 011 .

Strona 3 z 17