Prostokątny stół o wymiarach 2 m na 1 m można rozłożyć, tak aby przy dwóch krótszych bokach otrzymać półkola. Oblicz przybliżoną powierzchnię stołu. Przyjmij w obliczeniach 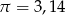 .
.
/Szkoła średnia/Zadania z treścią
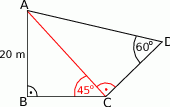
Pan Piotrek ma działkę w kształcie czworokąta, jak na rysunku. Oblicz powierzchnię tej działki. Wynik zaokrąglij do 1 m.
Funkcja o wzorze 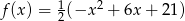 opisuje wydajność pracy robotnika w zależności od czasu pracy
opisuje wydajność pracy robotnika w zależności od czasu pracy  , w ciągu 8-godzinnego dnia pracy. Robotnik rozpoczyna pracę o godz.
, w ciągu 8-godzinnego dnia pracy. Robotnik rozpoczyna pracę o godz. 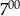 . O której godzinie jego wydajność jest największa?
. O której godzinie jego wydajność jest największa?
Wysokość prowizji, którą klient płaci w pewnym biurze maklerskim przy każdej zawieranej transakcji kupna lub sprzedaży akcji jest uzależniona od wartości transakcji. Zależność ta została przedstawiona w tabeli:
| Wartość transakcji | Wysokość prowizji |
| do 500 zł | 15 zł |
| od 500,01 zł do 3000 zł | 2% wartości transakcji + 5 zł |
| od 3000,01 zł do 8000 zł | 1,5% wartości transakcji + 20 zł |
| od 8000,01 zł do 15000 zł | 1% wartości transakcji + 60 zł |
| powyżej 15000 zł | 0,7% wartości transakcji + 105 zł |
Klient zakupił za pośrednictwem tego biura maklerskiego 530 akcji w cenie 25 zł za jedną akcję. Po roku sprzedał wszystkie kupione akcje po 45 zł za jedną sztukę. Oblicz, ile zarobił na tych transakcjach po uwzględnieniu prowizji, które zapłacił.
Woda może wpływać do basenu z dwóch kranów. Za pomocą pierwszego kranu basen można napełnić w czasie o 2 godziny dłuższym, a za pomocą drugiego kranu w czasie o 4,5 godziny dłuższym, niż przy napełnianiu basenu z wykorzystaniem obu kranów. W jakim czasie można napełnić ten basen odkręcając tylko pierwszy albo tylko drugi kran?
Woda może wpływać do basenu z dwóch kranów. Za pomocą pierwszego kranu basen można napełnić w czasie o 4 godziny dłuższym, a za pomocą drugiego kranu w czasie o 2,25 godziny dłuższym, niż przy napełnianiu basenu z wykorzystaniem obu kranów. W jakim czasie można napełnić ten basen odkręcając tylko pierwszy albo tylko drugi kran?
Liczebność kolonii bakterii pewnego szczepu w zależności od czasu opisuje funkcja 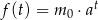 , gdzie
, gdzie 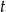 – oznacza czas obserwacji w godzinach,
– oznacza czas obserwacji w godzinach,  – pewną stałą dodatnią, a
– pewną stałą dodatnią, a 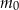 – liczebność początkowej próby bakterii. Na początku doświadczenia zaobserwowano 300 sztuk bakterii. Po dwóch godzinach liczba bakterii wzrosła do 1200. Po jakim czasie liczba bakterii wzrośnie do 153600?
– liczebność początkowej próby bakterii. Na początku doświadczenia zaobserwowano 300 sztuk bakterii. Po dwóch godzinach liczba bakterii wzrosła do 1200. Po jakim czasie liczba bakterii wzrośnie do 153600?
W 2000 roku pan Nowak wpłacił na rachunek bankowy kwotę 1000zł. Po 6 miesiącach ponownie wpłacił na ten rachunek 1000zł, a po upływie kolejnych 6 miesięcy podjął całą kwotę, która wraz z odsetkami wyniosła 2310zł. Oblicz, jakie było oprocentowanie tego rachunku w skali roku wiedząc, że nie ulegało ono zmianie, a bank kapitalizował odsetki co 6 miesięcy (w 2000 roku nie było podatku od odsetek).
W fabryce serów żółtych postanowiono od nowego roku produkować je w mniejszych bryłach i każdą krawędź serowych prostopadłościanów zmniejszono o 15%. Oblicz, o ile procent zmalała waga każdej bryły sera.
Sklep kupił za 8160 zł pewną ilość cukru. Gdy cukier potaniał o 4 gr na kilogramie, to za tę samą kwotę zakupiono o 80 kg cukru więcej. Ile kilogramów i po jakiej cenie za 1kg kupiono cukru za pierwszym razem?
Wojtek ułożył z drewnianych sześciennych klocków kwadrat (kładąc klocki jeden obok drugiego) i zostały mu 23 klocki. Następnie spróbował ułożyć kwadrat o boku o 1 klocek większym niż poprzedni i zabrakło mu 8 klocków. Ile klocków miał Wojtek?
W chwili początkowej 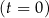 filiżanka z gorącą kawą znajduje się w pokoju, a temperatura tej kawy jest równa
filiżanka z gorącą kawą znajduje się w pokoju, a temperatura tej kawy jest równa 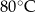 . Temperatura w pokoju (temperatura otoczenia) jest stała i równa
. Temperatura w pokoju (temperatura otoczenia) jest stała i równa 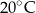 . Temperatura
. Temperatura 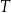 tej kawy zmienia się w czasie zgodnie z zależnością
tej kawy zmienia się w czasie zgodnie z zależnością
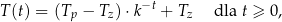
gdzie:
-
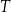 – temperatura kawy wyrażona w stopniach Celsjusza,
– temperatura kawy wyrażona w stopniach Celsjusza, -
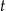 – czas wyrażony w minutach, liczony od chwili początkowej,
– czas wyrażony w minutach, liczony od chwili początkowej, -
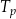 – temperatura początkowa kawy wyrażona w stopniach Celsjusza,
– temperatura początkowa kawy wyrażona w stopniach Celsjusza, -
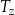 – temperatura otoczenia wyrażona w stopniach Celsjusza,
– temperatura otoczenia wyrażona w stopniach Celsjusza, -
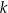 – stała charakterystyczna dla danej cieczy.
– stała charakterystyczna dla danej cieczy.
Po 10 minutach, licząc od chwili początkowej, kawa ostygła do temperatury 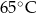 . Oblicz temperaturę tej kawy po następnych pięciu minutach. Wynik podaj w stopniach Celsjusza, w zaokrągleniu do jedności.
. Oblicz temperaturę tej kawy po następnych pięciu minutach. Wynik podaj w stopniach Celsjusza, w zaokrągleniu do jedności.
Drzewo wysokości 10 m rzuca cień długości 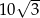 m. Oblicz miarę kąta, pod jakim promienie słoneczne padają do poziomu.
m. Oblicz miarę kąta, pod jakim promienie słoneczne padają do poziomu.
Pole powierzchni mieszkania jest równe 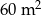 . Janek sporządził plan tego mieszkania. Jaką skalę zastosował Janek, jeśli pole powierzchni planu mieszkania było równe
. Janek sporządził plan tego mieszkania. Jaką skalę zastosował Janek, jeśli pole powierzchni planu mieszkania było równe 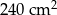 .
.
Wyznacz skalę mapy, na której jezioro o rzeczywistej powierzchni 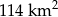 , zajmuje obszar
, zajmuje obszar 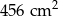 .
.
Zbiornik wodny o objętości 14700 litrów napełniono w całości wodą w następujący sposób. W ciągu pierwszej godziny nalano 800 litrów wody, a w ciągu każdej kolejnej godziny nalewano o 10 litrów mniej. Przez ile godzin napełniano zbiornik?
Gumową piłkę upuszczono z 81 metrów. Za każdym razem, po odbiciu piłka wznosi się na  wysokości, z której spadła.
wysokości, z której spadła.
- Znajdź największą wysokość piłki między 5 i 6 uderzeniem o podłoże.
- Jaką drogę pokona piłka zakładając, że odbija się ona 20 razy i po 20 odbiciu pozostaje na podłożu?
Pan Malinowski wziął kredyt na kupno samochodu w wysokości 20 000zł, który chce spłacać w rocznych ratach po 4 000zł każda. Do każdej raty dopisuje się odsetki w wysokości 26% tej kwoty, która została jeszcze do spłacenia przed wpłatą raty.
- Oblicz wysokość trzeciej i czwartej raty.
- Oblicz, jakim procentem kwoty spłaconej jest kwota pożyczona. Wynik zaokrąglij do części dziesiątych.
Karawana o długości 1 km jedzie przez pustynię z prędkością 4 km/h. Co jakiś czas od czoła karawany do jej końca i z powrotem jedzie goniec z prędkością 6 km/h. Oblicz długość drogi tam i z powrotem, którą pokonuje goniec. Oblicz, ile czasu zajmuje mu przebycie tej drogi.
Firma zajmująca się wynajmem lokali ma do dyspozycji 180 pomieszczeń użytkowych. Wszystkie pomieszczenia są zajęte wówczas, gdy koszt wynajmu za jeden miesiąc wynosi 1200 zł. Firma oszacowała, że każda kolejna podwyżka czynszu o 40 zł, zmniejsza o 5 liczbę wynajmowanych pomieszczeń. Jaki miesięczny koszt wynajmu powinna ustalić ta firma, aby jej przychód był maksymalny? Ile wynosi maksymalny przychód?
Na wycieczkę wyjechało 38 uczniów. Dzieci spały w 15 pokojach. Dziewczynki spały w pokojach dwuosobowych, a chłopcy spali w pokojach trzyosobowych. Wszystkie miejsca w pokojach były zajęte. Ile dziewczynek i ilu chłopców było na wycieczce? Zapisz obliczenia.
Każdy z 240 uczniów pewnej szkoły otrzymał 3 lub 4 darmowe bilety do kina. W sumie rozdano 880 biletów. Ilu uczniów otrzymało 3, a ilu 4 bilety? Zapisz obliczenia.
Liczbę 42 przedstaw w postaci sumy dwóch składników tak, by różnica ich kwadratów była równa 168.

