Zadania z treścią/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Zadania z treścią

Liczby mieszkańców (w przybliżeniu) Polski, Czech i Słowacji są w stosunku 390:103:54. Różnica liczb mieszkańców w Czechach i Słowacji jest równa 4,9 mln osób. Ilu mieszkańców jest w każdym z tych krajów?

Suma dwóch liczb jest równa 7 i jest o 2 mniejsza od ich iloczynu. Wyznacz te liczby.

Do zbiornika o pojemności 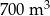3 700 m można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o 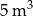5 m 3 wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 16 godzin krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.

Ukryj Podobne zadania

Do zbiornika o pojemności 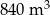3 840 m można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o 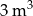3 m 3 wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 32 godziny krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.

Liczba jest o 3 większa od liczby 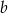. Iloraz liczb i 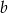jest dwa razy mniejszy od sumy tych liczb. Wyznacz liczby i .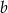

Liczba mieszkańców w pewnym mieście w ciągu ostatnich lat zwiększała się średnio o 0,8% rocznie i obecnie wynosi około 150000. Zakładając, że tempo wzrostu liczby mieszkańców się nie zmieni, oszacuj, ilu ludzi będzie mieszkać w tym mieście za 10lat.

Dwa pociągi towarowe wyjechały z miast 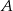i 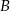oddalonych od siebie o 540 km. Pociąg jadący z miasta 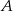do miasta 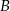wyjechał o godzinę wcześniej niż pociąg jadący z miasta 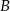do miasta 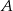i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.

Ukryj Podobne zadania

Dwa samochody osobowe wyjechały z miast 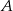i 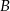oddalonych od siebie o 480 km. Samochód jadący z miasta 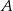do miasta 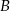wyjechał o pół godziny wcześniej niż samochód jadący z miasta 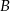do miasta 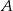i jechał z prędkością o 16 km/h mniejszą. Samochody te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te samochody.

Dwa motocykle wyjechały z miast 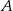i 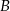oddalonych od siebie o 360 km. Motocykl jadący z miasta 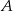do miasta 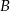wyjechał o 30 minut wcześniej niż motocykl jadący z miasta 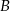do miasta 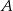i jechał z prędkością o 12 km/h mniejszą. Motocykle te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te motocykle.

Działka leśna zawierała przed 15 laty 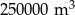3 250000 m drewna, a obecnie zawiera 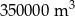35 0000 m 3 . O ile procent przeciętnie wzrasta ilość drewna na tej działce w ciągu roku? (Zakładamy stały przyrost procentowy.)

Uczeń kupił dwie książki za 100 zł, które po roku sprzedał z zyskiem 8%. Oblicz ile zapłacił za każdą z tych książek, jeżeli pierwszą z nich sprzedał z zyskiem 20%, drugą zaś ze stratą 10%.

Ukryj Podobne zadania

Uczeń kupił dwie książki za 150 zł, które po roku sprzedał z zyskiem 8%. Oblicz ile zapłacił za każdą z tych książek, jeżeli pierwszą z nich sprzedał ze stratą 10%, drugą zaś z zyskiem 20%.

Wyznacz dwie liczby całkowite różniące się o 6, których iloczyn jest możliwie najmniejszy.

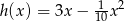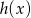Zawodnik kopnął piłkę, która zakreśliła w powietrzu fragment toru opisanego równaniem h (x) = 3x − 110x 2 ( oznacza poziomą odległość piłki od zawodnika, a h (x) wysokość na jakiej znajduje się piłka). Oblicz, na jaką największą wysokość wzniosła się piłka.

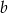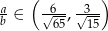Podaj przykład liczb naturalnych i takich, że a (--6- -3-) b ∈ √ 65,√15 .

Belki ułożono warstwami w ten sposób, że na dole jest 50 belek, w warstwie górnej 21, a każda kolejna warstwa zawiera o jedną belkę mniej niż warstwa niższa. Ile belek jest łącznie?

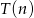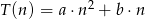Doświadczalnie ustalono, że czas T(n ) , liczony w sekundach, potrzebny na alfabetyczne ułożenie kartek z nazwiskami wyraża się, z dobrym przybliżeniem, wzorem T(n ) = a⋅ n2 + b⋅n . Ułożenie 10 kartek trwa średnio 20 sekund, a 30 kartek średnio 90 sekund. Wyznacz wzór funkcji 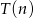T(n ) i oblicz, ile kartek można ułożyć średnio w ciągu 50 sekund.

W zalanej kopalni zainstalowano 3 pompy wypompowujące wodę z zalanych sztolni. Pierwsza pompa pracująca sama wypompowałaby wodę w ciągu 12 dni, druga w ciągu 15 dni, a trzecia 20 dni. Pierwsze trzy dni pierwsza i trzecia pompa pracowały wspólnie. Następnie włączono dodatkowo drugą pompę. Jak długo trwało wypompowywanie wody z kopalni?

Liczbę 7 dzielimy na trzy części tak aby pierwsza była dwa razy większa od drugiej. Jak należy dokonać podziału, aby suma kwadratów wszystkich trzech części była najmniejsza?

Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy większa od pierwszej. Wyznacz trzy liczby spełniające podane warunki tak, aby suma ich kwadratów była najmniejsza.

Nauczyciel zadał maturzystom serię zadań, które mieli rozwiązać w określonym terminie. Karol postanowił codziennie rozwiązywać tę samą liczbę zadań. Krzysiek obliczył, że jeśli dziennie będzie rozwiązywał o 2 zadania więcej od Karola, to skończy o 3 dni wcześniej niż Karol. Maciek postanowił rozwiązywać codziennie o 2 zadania więcej od Krzyśka i obliczył, że wszystkie zadania rozwiąże o 2 dni wcześniej niż Krzysiek. Ile zadań mieli do rozwiązania maturzyści?

Prostokątny stół o wymiarach 2 m na 1 m można rozłożyć, tak aby przy dwóch krótszych bokach otrzymać półkola. Oblicz przybliżoną powierzchnię stołu. Przyjmij w obliczeniach π = 3,14 .

Pan Piotrek ma działkę w kształcie czworokąta, jak na rysunku. Oblicz powierzchnię tej działki. Wynik zaokrąglij do 1 m.

Funkcja o wzorze 1 2 f(x) = 2(−x + 6x+ 21) opisuje wydajność pracy robotnika w zależności od czasu pracy , w ciągu 8-godzinnego dnia pracy. Robotnik rozpoczyna pracę o godz. 7 00 . O której godzinie jego wydajność jest największa?

Strona 6 z 17