Prostokątne zdjęcie o szerokości 30 cm i długości 45 cm oprawiono w prostokątną ramkę o jednakowej szerokości. Jaka jest szerokość ramki, jeśli pole zdjęcia wraz z ramką wynosi 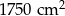 ?
?
/Szkoła średnia/Zadania z treścią
Prostokątne zdjęcie o szerokości 15 cm i długości 20 cm oprawiono w prostokątną ramkę o jednakowej szerokości. Jaka jest szerokość ramki, jeśli pole zdjęcia wraz z ramką wynosi 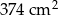 ?
?
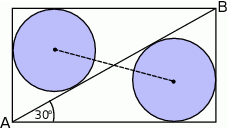
Na rysunku przedstawiony został szkic części parku. Dwie fontanny wpisano w prostokątny klomb kwiatów. Są one styczne do linii przekątnej klombu. Wiedząc, że przekątna klombu ma długość 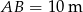 oraz tworzy ona z jednym z boków klombu kąt o mierze
oraz tworzy ona z jednym z boków klombu kąt o mierze 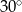 , wyznacz odległość środków tych fontann.
, wyznacz odległość środków tych fontann.
Deweloper oferuje możliwość kompletnego wyposażenia kuchni i salonu w ofercie „Malejące raty”. Wysokość pierwszej raty ustalono na 775 zł. Każda następna rata jest o 10 zł mniejsza od poprzedniej. Całkowity koszt wyposażenia kuchni i salonu ustalono na 30 240 zł. Oblicz wysokość ostatniej raty i liczbę wszystkich rat.
Dwie pracownice urzędu pocztowego miały ostemplować pewną partię listów. Stemplowanie listów pierwsza urzędniczka rozpoczęła o godzinie 8:00, a druga o godzinie 9:00. O godzinie 11:00 panie stwierdziły, że pozostało im jeszcze do ostemplowania 45% listów. Po ukończeniu pracy okazało się, że każda z urzędniczek ostemplowała tyle samo listów. Oblicz, w ciągu ilu godzin każda z pań ostemplowałaby sama wszystkie listy.
Tonę czystej platyny przetopiono w sześcian. Gęstość platyny jest równa 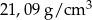 . Jak jest długość krawędzi platynowego sześcianu? Wynik podaj z dokładnością do 1 cm.
. Jak jest długość krawędzi platynowego sześcianu? Wynik podaj z dokładnością do 1 cm.
Wyznacz wszystkie liczby rzeczywiste, które są o 2 większe od swojej odwrotności.
30% pewnego towaru sprzedano z zyskiem 15-procentowym, a pozostałą część z zyskiem 10-procentowym. Jaki był ogólny zysk ze sprzedaży?
Czas 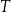 połowicznego rozpadu węgla
połowicznego rozpadu węgla 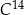 to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla
to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla 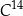 wynosi około
wynosi około 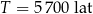 , a pozostała masa tego izotopu wyraża się wzorem
, a pozostała masa tego izotopu wyraża się wzorem
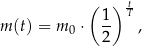
gdzie:
-
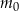 – masa izotopu węgla
– masa izotopu węgla 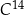 w trakcie życia organizmu
w trakcie życia organizmu -
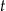 – czas jaki upłynął od czasu śmierci organizmu.
– czas jaki upłynął od czasu śmierci organizmu.
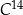 stanowi
stanowi 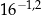 masy tego izotopu, jaka utrzymywała się podczas życia tego organizmu. Oblicz, ile lat mają odkryte szczątki organiczne.
masy tego izotopu, jaka utrzymywała się podczas życia tego organizmu. Oblicz, ile lat mają odkryte szczątki organiczne. Czas 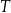 połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder
połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder 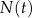 izotopu promieniotwórczego pozostających w próbce po czasie
izotopu promieniotwórczego pozostających w próbce po czasie 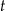 , licząc od chwili
, licząc od chwili 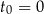 , wyraża się zależnością wykładniczą:
, wyraża się zależnością wykładniczą:
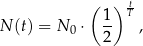
gdzie 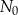 jest liczbą jąder izotopu promieniotwórczego w chwili początkowej
jest liczbą jąder izotopu promieniotwórczego w chwili początkowej 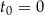 . Czas połowicznego rozpadu węgla
. Czas połowicznego rozpadu węgla 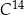 to około 5 700 lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla
to około 5 700 lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla 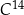 w pewnym organicznym znalezisku archeologicznym stanowi
w pewnym organicznym znalezisku archeologicznym stanowi 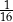 masy tego izotopu, jaka utrzymywała się podczas życia organizmu. Oblicz, ile lat ma opisane znalezisko archeologiczne. Wynik podaj z dokładnością do stu lat.
masy tego izotopu, jaka utrzymywała się podczas życia organizmu. Oblicz, ile lat ma opisane znalezisko archeologiczne. Wynik podaj z dokładnością do stu lat.
Na podstawie zasad dynamiki można udowodnić, że torem ruchu rzuconej piłki – przy pominięciu oporów powietrza – jest fragment paraboli. Koszykarz wykonał rzut do kosza z odległości 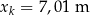 , licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie
, licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie 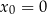 ,
, 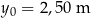 . Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:
. Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:
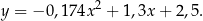
Rzut okazał się udany, a środek piłki przeszedł dokładnie przez środek kołowej obręczy kosza. Na rysunku poniżej przedstawiono tę sytuację oraz tor ruchu piłki w układzie współrzędnych.
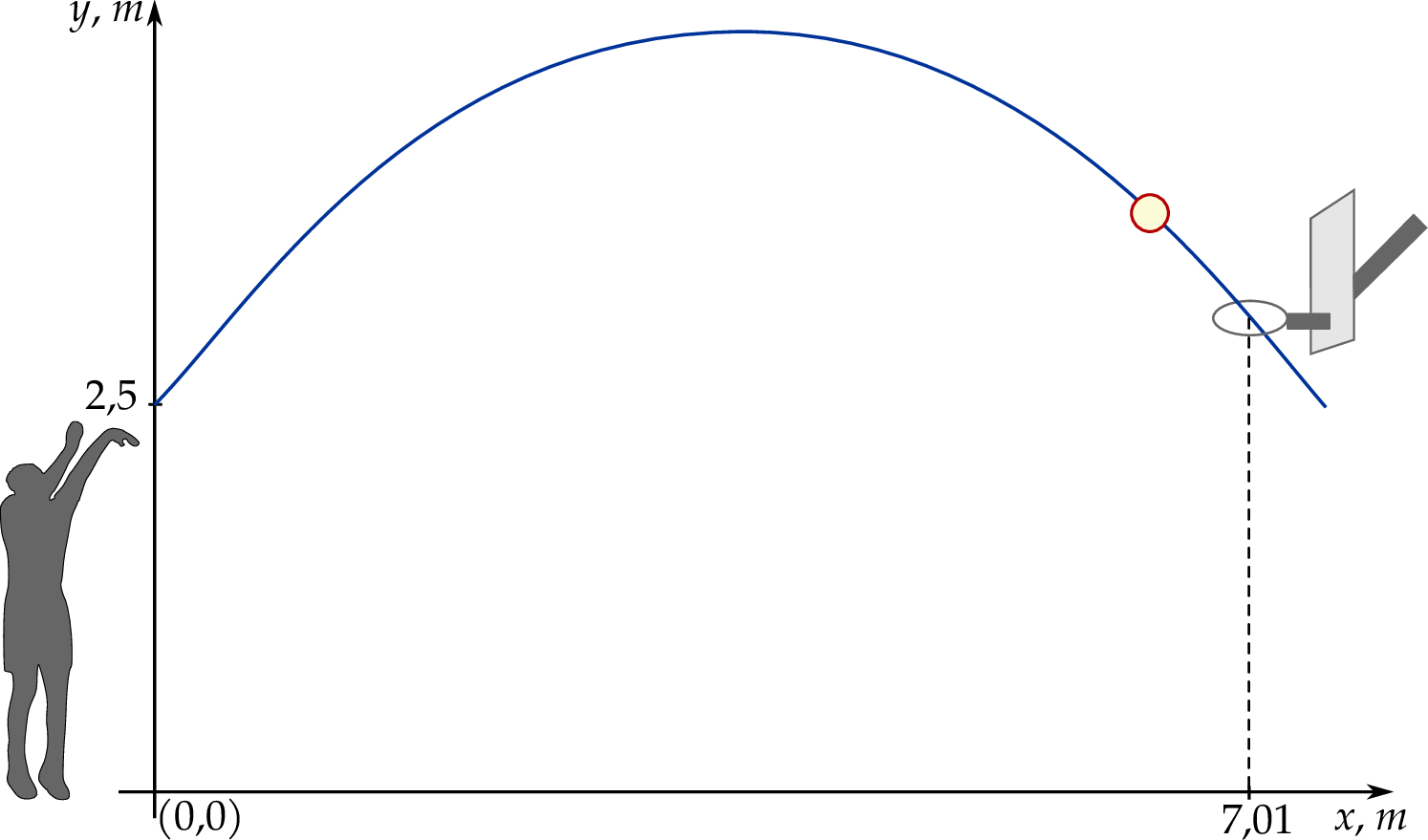
Oblicz wysokość maksymalną, na jaką wzniesie się środek piłki podczas opisanego rzutu. Wynik zapisz w metrach w zaokrągleniu do drugiego miejsca po przecinku.
W jakim stosunku należy zmieszać 14 i 6 procentowe roztwory chlorku sodu, aby otrzymać roztwór 8 procentowy?
Paweł i Gaweł wyruszyli w 500 kilometrową podróż dwoma samochodami. Samochód Pawła poruszał się cały czas ze stałą prędkością, a sposób poruszania się samochodu Gawła przedstawiony jest na poniższym wykresie.
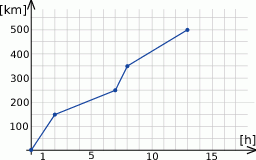
- Oblicz z jaką prędkością poruszał się samochód Pawła, jeżeli dojechał on do celu 20 minut po Gawle. Wynik podaj w kilometrach na godzinę
- Przez ile godzin Gaweł jechał wolniej od Pawła?
- Ile razy, i w której minucie podróży oba samochody się spotkały (nie licząc początku i końca podróży). Wynik podaj z dokładnością do 1 minuty.
W czasie wycieczki rowerowej uczniowie mieli do przebycia trasę długości 84 km. Podzielili tę trasę na odcinki równej długości i codziennie przejeżdżali wyznaczony odcinek. Gdyby na przebycie całej trasy zużyli o dwa dni więcej, to mogliby dziennie przejeżdżać o 7 km mniej. Ile kilometrów przebywali uczniowie dziennie i ile dni potrzebowali na pokonanie trasy?
Pewien turysta pokonał trasę 112 km, przechodząc każdego dnia tę samą liczbę kilometrów. Gdyby mógł przeznaczyć na tę wędrówkę o 3 dni więcej, to w ciągu każdego dnia mógłby przechodzić o 12 km mniej. Oblicz, ile kilometrów dziennie przechodził ten turysta.
Pan Kowalski zaciągnął w banku kredyt w wysokości 40000 zł. Oprocentowanie kredytu wynosi 12% w skali roku, a odsetki są dopisywane kwartalnie. Kredyt ma zostać spłacony w czterech równych ratach kwartalnych (spłacanych na koniec każdego kwartału). Wyznacz wysokość raty.
Z okrągłego obrusa o średnicy 2 m mama Jadzi chce zrobić kwadratowy obrus o boku 140 cm. Czy to będzie możliwe, jeśli kwadratowy obrus ma być z jednego kawałka materiału?
Z miejscowości 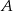 i
i 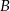 , które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.
, które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.
W wyborach do samorządu szkolnego uczniowie oddawali głos na jednego z trzech kandydatów: Adama, Olę albo Kasię. Wszystkie oddane głosy były ważne. Adam uzyskał 20% wszystkich głosów, a Ola 65%. Kasia otrzymała 72 głosy.
- Ilu uczniów brało udział w głosowaniu?
- O ile procent więcej głosów otrzymała Ola niż Adam?
W wyborach do samorządu szkolnego uczniowie oddawali głos na jednego z trzech kandydatów: Jacka, Pawła albo Anię. Wszystkie oddane głosy były ważne. Jacek uzyskał 25% wszystkich głosów, a Paweł 55%. Ania otrzymała 72 głosy.
- Ilu uczniów brało udział w głosowaniu?
- O ile procent więcej głosów otrzymał Paweł niż Jacek?
Szachownica do gry w szachy ma 64 pola. Przypuśćmy, że pierwsze pole ma wartość 1 grosza, drugie 2 groszy, trzecie 4 groszy, czwarte 8 groszy itd. Jaki jest jest najmniejszy numer pola szachownicy, którego wartość przekracza 1 000 000 zł?
W 1995 roku pan Nowak wpłacił 10000zł na dwuletnią lokatę z roczną kapitalizacją odsetek. Po roku bank obniżył roczną stopę procentową o dwa punkty procentowe. Po dwóch latach pan Nowak wypłacił całą kwotę, która wraz z odsetkami wyniosła 16640zł. Oblicz, jakie było oprocentowanie lokaty w pierwszym roku, a jakie w drugim (w latach 90-tych nie było podatku od odsetek).
Czas 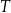 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 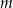 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
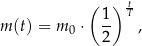
gdzie:
-
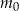 – masa przyjętej dawki leku,
– masa przyjętej dawki leku, -
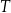 – czas półtrwania leku,
– czas półtrwania leku, -
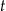 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pacjent otrzymuje co 4 dni o tej samej godzinie dawkę 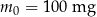 leku L. Czas półtrwania tego leku w organizmie jest równy
leku L. Czas półtrwania tego leku w organizmie jest równy 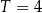 doby.
doby.
Oblicz masę leku L w organizmie tego pacjenta tuż przed przyjęciem jedenastej dawki tego leku. Wynik podaj w zaokrągleniu do 0,1 mg.
Czas 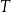 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 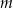 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
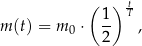
gdzie:
-
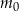 – masa przyjętej dawki leku
– masa przyjętej dawki leku -
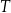 – czas półtrwania leku
– czas półtrwania leku -
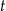 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pan Karol otrzymuje codziennie o godz. 12:00 dawkę 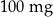 leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę
leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 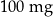 tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy
tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 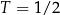 doby.
doby.
Oblicz masę leku L w organizmie pana Tomasza tuż przed przyjęciem szóstej dawki tego leku. Wynik podaj w zaokrągleniu do 0,01 mg.
Do basenu zawierającego 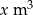 wody doprowadzono pierwszego dnia
wody doprowadzono pierwszego dnia 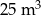 wody, po czym każdego dnia doprowadzano o
wody, po czym każdego dnia doprowadzano o 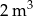 wody więcej niż dnia poprzedniego. Równocześnie z basenu ubywa codziennie
wody więcej niż dnia poprzedniego. Równocześnie z basenu ubywa codziennie 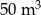 wody.
wody.
- Jaka musi być początkowa ilość wody w basenie, aby w tych warunkach basen nigdy nie został opróżniony?
- Po ilu dniach basen będzie zawierał najmniejszą ilość wody?

