Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
/Szkoła średnia/Geometria/Planimetria
Trójkąt równoboczny, kwadrat i sześciokąt foremny mają ten sam obwód długości 10cm. Oblicz pole każdej z tych figur. Która z nich ma największe pole, a która najmniejsze?
W trapezie 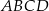 mamy
mamy 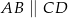 oraz
oraz 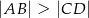 . Punkt
. Punkt 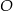 jest środkiem ramienia
jest środkiem ramienia 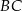 , a punkt
, a punkt 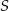 jest punktem wspólnym prostych
jest punktem wspólnym prostych 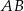
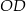 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 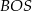 jest równe polu trójkąta
jest równe polu trójkąta 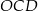 .
.
Liczby 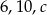 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
W okręgu narysowano dwie średnice 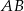 i
i 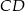 . Udowodnij, że czworokąt
. Udowodnij, że czworokąt 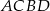 jest prostokątem.
jest prostokątem.
Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o 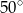 . Oblicz kąty tego trójkąta.
. Oblicz kąty tego trójkąta.
Jeden z kątów trójkąta jest trzy razy większy od drugiego oraz o 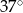 większy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
większy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
Jeden z kątów trójkąta jest cztery razy mniejszy od mniejszego z dwóch pozostałych kątów, które różnią się o 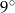 . Oblicz kąty tego trójkąta.
. Oblicz kąty tego trójkąta.
Jeden z kątów trójkąta jest cztery razy większy od drugiego oraz o 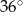 mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
Obwód prostokąta wynosi 60 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Wyznacz kąt pomiędzy przekątną, a dłuższym bokiem prostokąta. Wynik podaj z dokładnością do 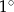 .
.
Obwód prostokąta wynosi 32 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Wyznacz kąt pomiędzy przekątną, a dłuższym bokiem prostokąta. Wynik podaj z dokładnością do 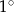 .
.
Dany jest trapez równoramienny 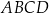 , w którym podstawa
, w którym podstawa 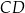 ma długość 6, ramię
ma długość 6, ramię 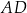 ma długość 4, a kąty
ma długość 4, a kąty 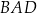 oraz
oraz  mają miarę
mają miarę  (zobacz rysunek).
(zobacz rysunek).
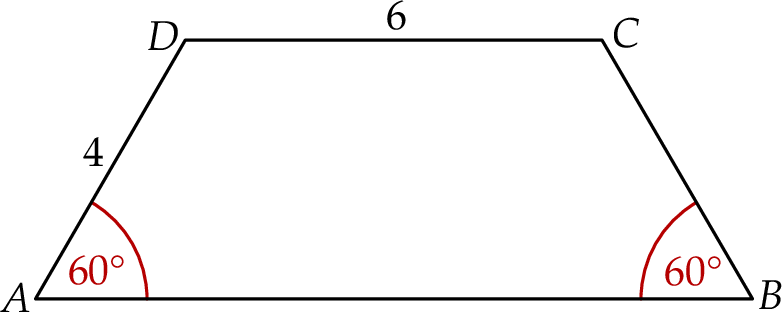
Oblicz pole tego trapezu.
Dany jest trapez równoramienny  , w którym podstawa
, w którym podstawa 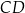 ma długość 8, ramię
ma długość 8, ramię 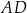 ma długość 6, a kąty
ma długość 6, a kąty 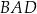 oraz
oraz 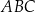 mają miarę
mają miarę 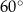 (zobacz rysunek).
(zobacz rysunek).
Oblicz pole tego trapezu.
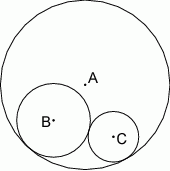
Na rysunku okręgi o środkach  i
i  są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie
są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie 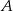 . Wykaż, że jeśli
. Wykaż, że jeśli 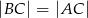 , to długość odcinka
, to długość odcinka 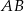 jest równa długości średnicy okręgu o środku w punkcie
jest równa długości średnicy okręgu o środku w punkcie 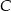 .
.
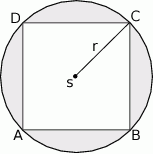
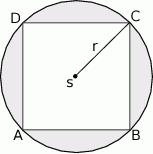
Na kwadracie 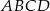 opisano okrąg o promieniu
opisano okrąg o promieniu 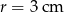 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
Na kwadracie 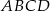 opisano okrąg o promieniu
opisano okrąg o promieniu 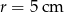 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
Wyznacz wartości funkcji trygonometrycznych kątów ostrych trójkąta powstałego wskutek połączenia odcinkiem wierzchołka kwadratu ze środkiem przeciwległego boku.
Trójkąt o bokach 6, 8 i 10 jest podobny do trójkąta o obwodzie 216. Oblicz długości boków drugiego trójkąta.
Trójkąt o bokach 12, 9 i 15 jest podobny do trójkąta o obwodzie 108. Oblicz długości boków drugiego trójkąta.
Obwód rombu wynosi 68 cm, a długość jednej z jego przekątnych stanowi 187,5% długości drugiej przekątnej. Oblicz pole tego rombu.
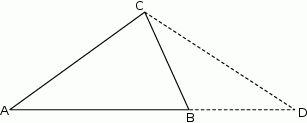
W trójkącie  przedłużono bok
przedłużono bok 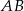 poza wierzchołek
poza wierzchołek 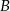 i odłożono odcinek
i odłożono odcinek 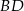 taki, że
taki, że 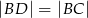 . Następnie połączono punkty
. Następnie połączono punkty 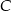 i
i 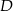 (rysunek). Wykaż, że
(rysunek). Wykaż, że 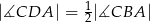 .
.
W trójkącie 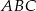 przedłużono bok
przedłużono bok 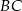 poza wierzchołek
poza wierzchołek 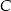 i odłożono odcinek
i odłożono odcinek 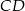 taki, że
taki, że 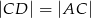 . Następnie połączono punkty
. Następnie połączono punkty 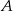 i
i 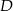 (rysunek). Wykaż, że
(rysunek). Wykaż, że 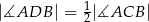 .
.
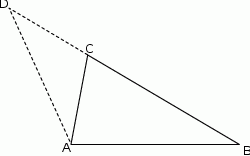
W kole poprowadzono cięciwę i średnicę. Cięciwa dzieli średnicę na odcinki o długościach 2 oraz 10 i tworzy z nią kąt o mierze 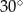 . Oblicz odległość środka okręgu od cięciwy.
. Oblicz odległość środka okręgu od cięciwy.
Kąt wpisany w koło ma miarę 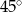 i jest oparty na łuku długości
i jest oparty na łuku długości 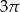 . Oblicz pole wycinka koła wyznaczonego przez ten sam łuk.
. Oblicz pole wycinka koła wyznaczonego przez ten sam łuk.
Punkty 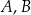 należą do jednego ramienia kąta o wierzchołku
należą do jednego ramienia kąta o wierzchołku 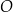 , a punkty
, a punkty 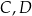 należą do jego drugiego ramienia i wiadomo, że
należą do jego drugiego ramienia i wiadomo, że 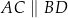 . Wyznacz
. Wyznacz 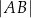 , jeśli wiadomo, że
, jeśli wiadomo, że 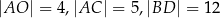 .
.
Na dwusiecznej 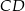 trójkąta
trójkąta 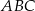 , w którym
, w którym 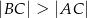 wybrano punkt
wybrano punkt 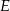 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 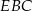 jest większe od pola trójkąta
jest większe od pola trójkąta 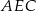 .
.
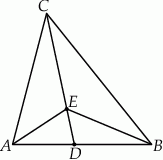
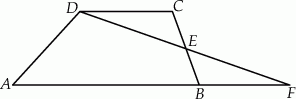
Na rysunku przedstawiono trapez  i trójkąt
i trójkąt  . Punkt
. Punkt  leży w połowie odcinka
leży w połowie odcinka 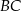 . Uzasadnij, że pole trapezu
. Uzasadnij, że pole trapezu 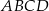 i pole trójkąta
i pole trójkąta 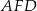 są równe.
są równe.
W trójkącie prostokątnym, w którym przyprostokątne mają długości 2 i 4, jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 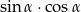 .
.
W trójkącie prostokątnym przyprostokątne mają długości 1 i 3, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 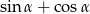 .
.
W trójkącie prostokątnym przyprostokątne mają długości 2 i 4, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 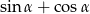 .
.
W trójkącie prostokątnym przyprostokątne mają długości 3 i 5, a jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 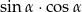 .
.
W trójkącie prostokątnym przyprostokątne mają długości 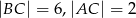 . Wyznacz wartość wyrażenia
. Wyznacz wartość wyrażenia 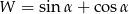 , gdzie
, gdzie  jest najmniejszym kątem ostrym tego trójkąta.
jest najmniejszym kątem ostrym tego trójkąta.

