Pierwiastkami wielomianu 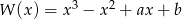 są tylko dwie liczby: 2 oraz (-3).
są tylko dwie liczby: 2 oraz (-3).
- Oblicz
 i
i 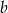 .
. - Zapisz wielomian w postaci czynników liniowych.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pierwiastkami wielomianu 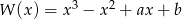 są tylko dwie liczby: 2 oraz (-3).
są tylko dwie liczby: 2 oraz (-3).
 i
i 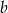 .
. Liczby 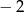 i 3 są pierwiastkami wielomianu
i 3 są pierwiastkami wielomianu 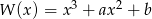 . Wyznacz liczby
. Wyznacz liczby  i
i 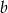 oraz trzeci pierwiastek wielomianu.
oraz trzeci pierwiastek wielomianu.
Liczby 2 i 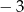 są pierwiastkami wielomianu
są pierwiastkami wielomianu 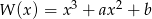 . Wyznacz liczby
. Wyznacz liczby  i
i 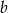 oraz trzeci pierwiastek wielomianu.
oraz trzeci pierwiastek wielomianu.
Wielomian 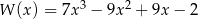 ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek.
ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek.
Wiedząc, że liczba 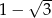 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 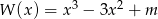 , wyznacz wartość parametru
, wyznacz wartość parametru 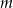 .
.
Wykaż, że dla dowolnej wartości parametru  równanie
równanie
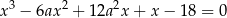
ma dokładnie jedno rozwiązanie rzeczywiste.
Rozwiąż równanie 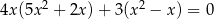 .
.
Miejscem zerowym wielomianu 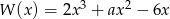 jest liczba
jest liczba 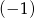 .
.
 .
. 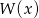 .
.