Wielomian 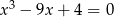 ma 3 pierwiastki rzeczywiste.
ma 3 pierwiastki rzeczywiste.
- Oblicz sumę odwrotności tych pierwiastków.
- Ustal, ile jest pierwiastków dodatnich.
- Oblicz odwrotność sumy kwadratów pierwiastków.
- Oblicz sumę kwadratów odwrotności tych pierwiastków.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wielomian 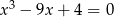 ma 3 pierwiastki rzeczywiste.
ma 3 pierwiastki rzeczywiste.
Rozwiąż równanie 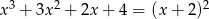 .
.
Rozwiąż równanie 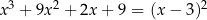 .
.
Rozwiąż równanie 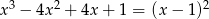 .
.
Rozwiąż równanie 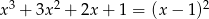 .
.
Rozwiąż równanie 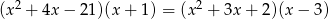 .
.
Rozwiąż równanie 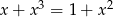 .
.
Rozwiąż równanie 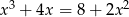 .
.
Dla jakich wartości parametru 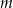 równanie
równanie 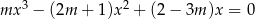 ma rozwiązania, których suma jest dodatnia?
ma rozwiązania, których suma jest dodatnia?
Rozwiąż równanie 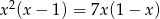 .
.
Rozwiąż równanie 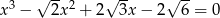 .
.
Rozwiąż równanie 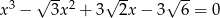 .
.
Wyznacz wszystkie wartości parametru 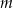 , dla których równanie
, dla których równanie
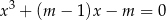
ma dokładnie dwa pierwiastki rzeczywiste. Dla otrzymanych wartości 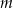 wyznacz te pierwiastki.
wyznacz te pierwiastki.
Wielomian 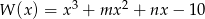 ma trzy pierwiastki
ma trzy pierwiastki 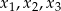 , przy czym
, przy czym 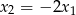 i
i 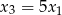 . Wyznacz
. Wyznacz 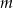 i
i  .
.
Wielomian 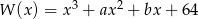 ma trzy pierwiastki:
ma trzy pierwiastki: 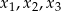 , przy czym
, przy czym 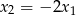 i
i 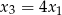 . Wyznacz
. Wyznacz  i
i 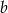 .
.
Równanie 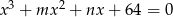 ma trzy pierwiastki będące kolejnymi wyrazami ciągu geometrycznego o ilorazie
ma trzy pierwiastki będące kolejnymi wyrazami ciągu geometrycznego o ilorazie 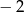 . Wyznacz
. Wyznacz 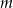 i
i  .
.
Rozwiąż równanie 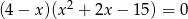 .
.
Rozwiąż równanie 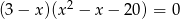 .
.
Liczba 3 jest pierwiastkiem wielomianu 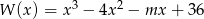 . Wyznacz parametr
. Wyznacz parametr 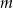 i pozostałe pierwiastki tego wielomianu.
i pozostałe pierwiastki tego wielomianu.
Dany jest wielomian 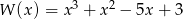 .
.
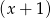 .
. 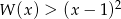 .
.Wielomian 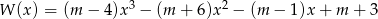 jest podzielny przez dwumian
jest podzielny przez dwumian 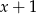 . Dla jakich wartości parametru
. Dla jakich wartości parametru 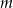 wielomian
wielomian 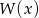 ma dokładnie dwa pierwiastki?
ma dokładnie dwa pierwiastki?
Wiedząc, że suma kwadratów pierwiastków równania
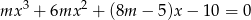
jest równa 30, wyznacz 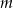 .
.
Sprawdź dla jakiego 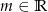 pierwiastki wielomianu
pierwiastki wielomianu 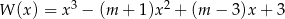 tworzą ciąg arytmetyczny?
tworzą ciąg arytmetyczny?
Wyznacz wszystkie wartości parametru 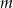 , dla których jedynym rozwiązaniem rzeczywistym równania
, dla których jedynym rozwiązaniem rzeczywistym równania 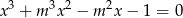 jest liczba 1.
jest liczba 1.
Dany jest wielomian 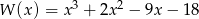 .
.
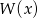 i
i 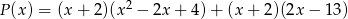 są równe.
są równe. 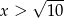 , to
, to 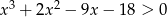 .
.Pierwiastkiem wielomianu 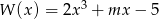 jest liczba -2. Wyznacz parametr
jest liczba -2. Wyznacz parametr 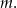
Pierwiastkiem wielomianu 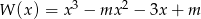 jest liczba
jest liczba 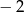 . Wyznacz parametr
. Wyznacz parametr 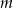 .
.
Dane są liczby wymierne 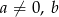 i
i 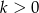 takie, że liczby
takie, że liczby 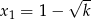 i
i 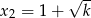 są pierwiastkami równania
są pierwiastkami równania 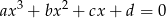 . Wykaż, że
. Wykaż, że  i
i 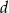 są liczbami wymiernymi.
są liczbami wymiernymi.
Dany jest wielomian 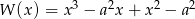 , gdzie
, gdzie 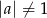 .
.
 , dla której suma kwadratów pierwiastków wielomianu
, dla której suma kwadratów pierwiastków wielomianu 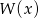 jest możliwie najmniejsza.
jest możliwie najmniejsza.Dany jest wielomian 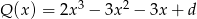 .
.
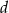 .
. 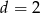 przedstaw wielomian
przedstaw wielomian 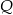 w postaci iloczynu wielomianów stopnia pierwszego.
w postaci iloczynu wielomianów stopnia pierwszego.