Wyznacz współczynniki  i
i 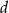 wielomianu
wielomianu 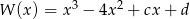 wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu
wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu 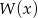 .
.
/Szkoła średnia/Równania/Wielomianowe/Stopnia 3
Jedynym rozwiązaniem wymiernym równania 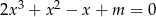 , gdzie
, gdzie 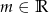 , jest liczba
, jest liczba 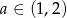 . Wyznacz liczbę
. Wyznacz liczbę 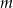 oraz pozostałe pierwiastki wielomianu.
oraz pozostałe pierwiastki wielomianu.
Rozwiąż równanie 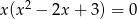 .
.
Rozwiąż równanie 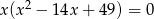 .
.
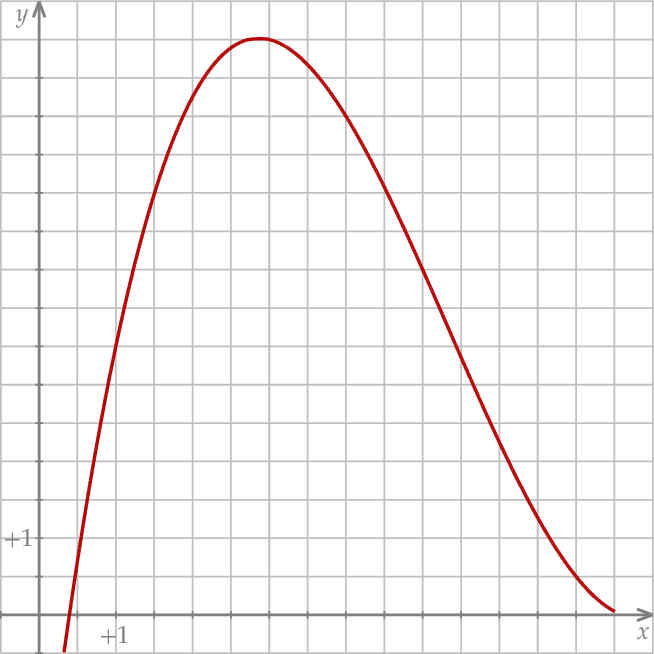
Na rysunku przedstawiono fragment wykresu wielomianu 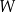 określonego wzorem
określonego wzorem
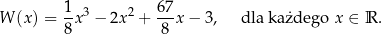
Oblicz wszystkie pierwiastki wielomianu 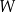 .
.
Udowodnij, że jeżeli wielomian 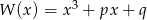 ma trzy pierwiastki, to
ma trzy pierwiastki, to 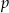 jest liczbą ujemną.
jest liczbą ujemną.
Rozwiąż równanie 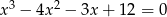 .
.
Rozwiąż równanie 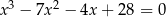 .
.
Rozwiąż równanie 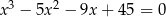 .
.
Rozwiąż równanie 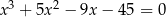 .
.
Rozwiąż równanie 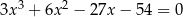 .
.
Rozwiąż równanie 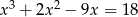 .
.
Rozwiąż równanie 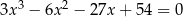 .
.
Rozwiąż równanie 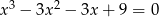 .
.
Rozwiąż równanie 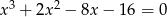 .
.
Rozwiąż równanie 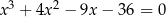 .
.
Rozwiąż równanie 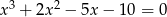 .
.
Rozwiąż równanie 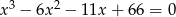 .
.
Rozwiąż równanie 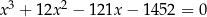 .
.
Rozwiąż równanie 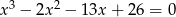 .
.
Rozwiąż równanie 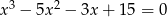 .
.
Rozwiąż równanie 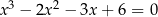 .
.
Rozwiąż równanie 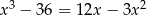 .
.
Rozwiąż równanie 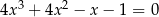 .
.
Rozwiąż równanie 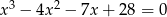 .
.
Rozwiąż równanie 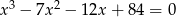 .
.
Rozwiąż równanie 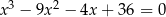 .
.
Rozwiąż równanie 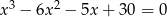 .
.
Rozwiąż równanie 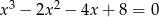 .
.
Rozłóż na czynniki liniowe wielomian 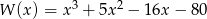 .
.
Rozwiąż równanie 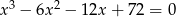 .
.
Rozwiąż równanie 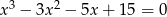 .
.
Rozwiąż równanie 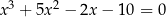 .
.
Rozwiąż równanie 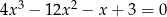 .
.
Rozwiąż równanie 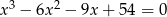 .
.
Dla jakich wartości parametru 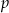 wielomian
wielomian 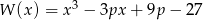 ma trzy różne pierwiastki rzeczywiste?
ma trzy różne pierwiastki rzeczywiste?
Wyznacz wszystkie wartości parametru 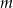 , dla którego wielomian
, dla którego wielomian 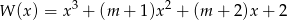 ma trzy różne pierwiastki rzeczywiste.
ma trzy różne pierwiastki rzeczywiste.
Wyznacz wszystkie wartości parametru 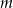 , dla których liczba 1 jest jedynym całkowitym pierwiastkiem wielomianu
, dla których liczba 1 jest jedynym całkowitym pierwiastkiem wielomianu 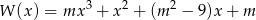 .
.
Wyznacz wszystkie wartości parametru 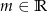 , dla których pierwiastki wielomianu
, dla których pierwiastki wielomianu 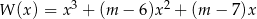 tworzą ciąg arytmetyczny.
tworzą ciąg arytmetyczny.
Rozwiąż równanie 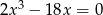 .
.
Wyznacz wszystkie wartości parametru 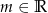 , dla których równanie
, dla których równanie
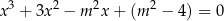
ma trzy różne pierwiastki, z których jeden jest ujemny, a pozostałe dwa należą do przedziału ![[ ] 1 2 ,5](https://img.zadania.info/zad/4913698/HzadT2x.png) .
.
Rozwiąż nierówność 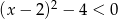 . Podaj wszystkie rozwiązania równania
. Podaj wszystkie rozwiązania równania 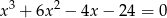 , które należą do zbioru rozwiązań tej nierówności.
, które należą do zbioru rozwiązań tej nierówności.
Dla jakich wartości parametru 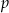 wielomian
wielomian 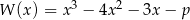 ma trzy pierwiastki rzeczywiste?
ma trzy pierwiastki rzeczywiste?
Dany jest wielomian 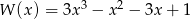 .
.
- Rozłóż wielomian na czynniki liniowe.
- Rozwiąż nierówność
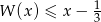 .
.
Dany jest wielomian 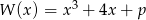 , gdzie
, gdzie 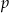 jest liczbą pierwszą. Wyznacz
jest liczbą pierwszą. Wyznacz 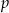 wiedząc, że
wiedząc, że 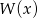 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Wykaż, że jeżeli wielomian 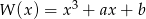 ma pierwiastek dwukrotny, to
ma pierwiastek dwukrotny, to 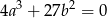 .
.
Wyznacz te wartości parametru 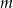 , dla których równanie
, dla których równanie 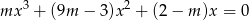 ma co najmniej jedno rozwiązanie dodatnie.
ma co najmniej jedno rozwiązanie dodatnie.
Znajdź te wartości parametru 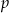 , dla których równanie
, dla których równanie 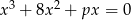 ma trzy różne rozwiązania.
ma trzy różne rozwiązania.
Dane jest równanie ![2 2 (x + 3)[x + (p + 4)x + (p + 1 ) ] = 0](https://img.zadania.info/zad/6258301/HzadT0x.gif) z niewiadomą
z niewiadomą  .
.
- Rozwiąż to równanie dla
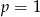 .
. - Wyznacz wszystkie wartości parametru
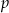 , dla których równanie to ma tylko jedno rozwiązanie.
, dla których równanie to ma tylko jedno rozwiązanie.
Wyznacz wszystkie wartości parametru 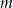 , dla których równanie
, dla których równanie
![2 2 (x+ 2)[x − (m + 1)x − 6m + 3m )] = 0](https://img.zadania.info/zad/2956182/HzadT1x.gif)
ma dokładnie dwa rozwiązania.
Wyznacz te wartości parametru 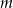 , dla których równanie
, dla których równanie
![2 2 (x− 3)[x − 2(2m + 1 )x+ (m + 2) ] = 0](https://img.zadania.info/zad/8529863/HzadT1x.gif)
ma trzy różne rozwiązania.
Wyznacz wszystkie wartości parametru 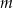 , dla których równanie
, dla których równanie
![2 2 (x− 3)[x + (m − 1)x − 6m + 2m )] = 0](https://img.zadania.info/zad/1637258/HzadT1x.gif)
ma dokładnie dwa rozwiązania.
Rozwiąż równanie 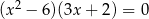 .
.
Rozwiąż równanie 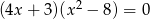 .
.

