Określ liczbę pierwiastków równania 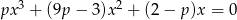 w zależności od wartości parametru
w zależności od wartości parametru 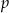 . Naszkicuj wykres funkcji, która każdej wartości parametru
. Naszkicuj wykres funkcji, która każdej wartości parametru 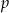 przyporządkowuje liczbę pierwiastków tego równania.
przyporządkowuje liczbę pierwiastków tego równania.
/Szkoła średnia/Równania/Wielomianowe/Stopnia 3
Liczba  jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 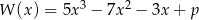 . Wyznacz pozostałe pierwiastki tego wielomianu i rozwiąż nierówność
. Wyznacz pozostałe pierwiastki tego wielomianu i rozwiąż nierówność 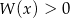 .
.
Wielomian 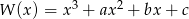 ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy
ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy 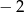 . Oblicz współczynniki
. Oblicz współczynniki 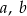 i
i  wiedząc, że
wiedząc, że 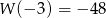 .
.
Jednym z pierwiastków wielomianu 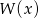 stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu tego wielomianu należy punkt
stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu tego wielomianu należy punkt 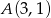 . Wiedząc, że reszta z dzielenia wielomianu
. Wiedząc, że reszta z dzielenia wielomianu 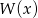 przez dwumian
przez dwumian 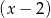 jest równa
jest równa 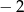 , wyznacz wzór tego wielomianu.
, wyznacz wzór tego wielomianu.
Rozwiąż równanie 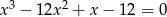 .
.
Rozwiąż równanie 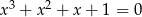 .
.
Rozwiąż równanie 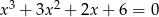 .
.
Rozwiąż równanie 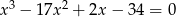 .
.
Rozwiąż równanie 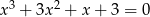 .
.
Rozwiąż równanie 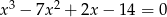 .
.
Rozwiąż równanie 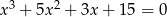 .
.
Rozwiąż równanie 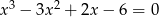 .
.
Pierwiastki równania 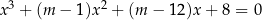 z niewiadomą
z niewiadomą  tworzą trzywyrazowy ciąg geometryczny. Oblicz
tworzą trzywyrazowy ciąg geometryczny. Oblicz 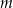 oraz sumę kwadratów tych pierwiastków.
oraz sumę kwadratów tych pierwiastków.
Dane są liczby wymierne 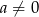 i
i 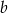 takie, że równanie
takie, że równanie 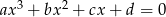 ma dwa pierwiastki wymierne. Wykaż, że
ma dwa pierwiastki wymierne. Wykaż, że  i
i 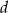 są liczbami wymiernymi.
są liczbami wymiernymi.
Dany jest wielomian 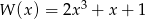
- Uzasadnij, że wielomian
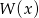 nie ma dodatnich pierwiastków.
nie ma dodatnich pierwiastków. - Uzasadnij, że wielomian
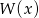 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych. - Uzasadnij, że wielomian
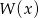 ma co najmniej jeden pierwiastek.
ma co najmniej jeden pierwiastek.
Wiedząc, że wielomian 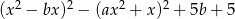 jest wielomianem stopnia 3 oraz 1 jest jego pierwiastkiem wyznacz
jest wielomianem stopnia 3 oraz 1 jest jego pierwiastkiem wyznacz  i
i 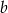 .
.
Znajdź wszystkie wartości parametru 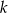 , dla których równanie
, dla których równanie 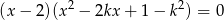 ma więcej niż jeden pierwiastek.
ma więcej niż jeden pierwiastek.
Wielomian 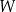 jest określony wzorem
jest określony wzorem 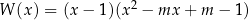 dla każdego
dla każdego 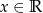 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 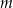 , dla których wielomian
, dla których wielomian 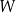 ma dokładnie jeden pierwiastek rzeczywisty.
ma dokładnie jeden pierwiastek rzeczywisty.
Rozwiąż równanie 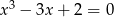 .
.
Rozwiąż równanie 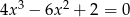 .
.
Rozwiąż równanie 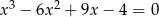 .
.
Wyznacz wszystkie wartości parametru 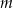 , dla których równanie
, dla których równanie
![2 2 (x − 4 )[x + (m − 3)x + m − m − 6] = 0](https://img.zadania.info/zad/7940380/HzadT1x.gif)
ma trzy różne rozwiązania rzeczywiste 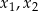 oraz
oraz 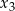 , spełniające warunek
, spełniające warunek
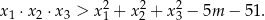
Dane jest równanie
![2 (x − 6) ⋅[(m − 2)x − 4(m + 3)x + m + 1] = 0](https://img.zadania.info/zad/4031216/HzadT0x.gif)
z niewiadomą  i parametrem
i parametrem 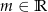 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 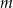 , dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
, dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Wyznacz wszystkie wartości parametru 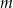 , dla których równanie
, dla których równanie
![2 2 (x − 3)[x + (m − 9)x + m − m + 16] = 0](https://img.zadania.info/zad/6498821/HzadT1x.gif)
ma trzy różne rozwiązania rzeczywiste 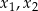 oraz
oraz 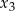 , spełniające warunek
, spełniające warunek
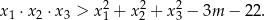
Dane jest równanie
![2 (x − 2 )⋅[(m − 7)x + 2(m + 3 )x− (2m + 3)] = 0](https://img.zadania.info/zad/8155916/HzadT0x.gif)
z niewiadomą  i parametrem
i parametrem 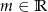 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 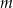 , dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
, dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Liczby 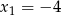 i
i 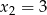 są pierwiastkami wielomianu
są pierwiastkami wielomianu 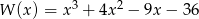 . Oblicz trzeci pierwiastek tego wielomianu.
. Oblicz trzeci pierwiastek tego wielomianu.
Wyznacz wartość parametru 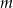 , dla którego równanie
, dla którego równanie
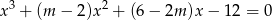
ma trzy pierwiastki 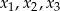 spełniające warunki
spełniające warunki 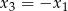 oraz
oraz 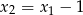 .
.
Rozwiąż równanie 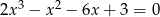 .
.
Rozwiąż równanie 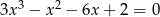 .
.
Rozwiąż równanie 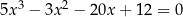 .
.
Rozwiąż równanie 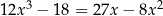 .
.
Rozwiąż równanie 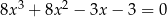 .
.
Rozwiąż równanie 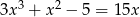 .
.
Rozwiąż równanie 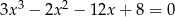 .
.
Wyznacz pierwiastki wielomianu 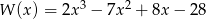 .
.
Rozwiąż równanie 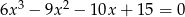 .
.
Rozwiąż równanie 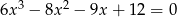 .
.
Rozwiąż równanie 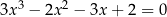 .
.
Rozwiąż równanie 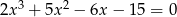 .
.
Rozwiąż równanie 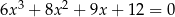 .
.
Rozwiąż równanie 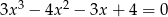 .
.
Rozwiąż równanie
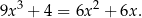
Rozwiąż równanie
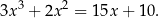
Rozwiąż równanie 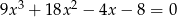 .
.
Rozwiąż równanie 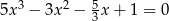 .
.
Rozwiąż równanie 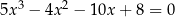 .
.
Rozwiąż równanie
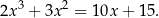
Rozwiąż równanie 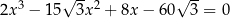 .
.
Rozwiąż równanie 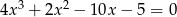 .
.
Rozwiąż równanie 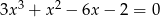 .
.
Rozwiąż równanie 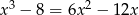 .
.
Rozwiąż równanie 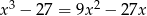 .
.
Rozwiąż równanie 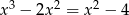 .
.
Dany jest wielomian 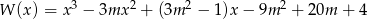 . Wykres tego wielomianu, po przesunięciu o wektor
. Wykres tego wielomianu, po przesunięciu o wektor ![→ u = [− 3,0]](https://img.zadania.info/zad/8700545/HzadT1x.gif) , przechodzi przez początek układu współrzędnych. Wyznacz wszystkie pierwiastki wielomianu
, przechodzi przez początek układu współrzędnych. Wyznacz wszystkie pierwiastki wielomianu 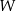 .
.
Suma wszystkich czterech współczynników wielomianu 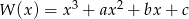 jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 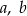 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Współczynniki wielomianu 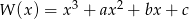 spełniają warunek:
spełniają warunek: 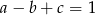 . Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 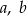 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Wielomian 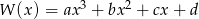 , gdzie
, gdzie 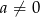 , ma dwa różne miejsca zerowe:
, ma dwa różne miejsca zerowe: 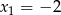 oraz
oraz 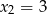 , przy czym pierwiastek
, przy czym pierwiastek 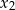 jest dwukrotny. Dla argumentu 1 wartość wielomianu jest równa
jest dwukrotny. Dla argumentu 1 wartość wielomianu jest równa 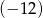 .
.
- Wyznacz wartości współczynników
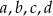 .
. - Dla wyznaczonych współczynników rozwiąż nierówność
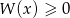 .
.
Dany jest wielomian 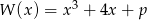 , gdzie
, gdzie 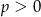 jest liczbą pierwszą. Znajdź
jest liczbą pierwszą. Znajdź 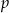 wiedząc, że
wiedząc, że 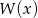 ma pierwiastek całkowity.
ma pierwiastek całkowity.

