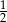W wycieczce szkolnej wzięło udział 12 dziewcząt i 8 chłopców z klasy Va, 13 chłopców i 11 dziewcząt z klasy Vb oraz czworo nauczycieli. Prawdopodobieństwo, że losowo wybrany uczestnik wycieczki jest chłopcem z klasy Va, jest równe
A)  B)
B) 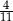 C)
C) 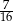 D)
D) 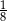
/Szkoła podstawowa/Zadania testowe/Prawdopodobieństwo
Doświadczenie losowe polega na czterokrotnym rzucie symetryczną monetą. Jeśli w pierwszych trzech rzutach wypadnie orzeł, to w czwartym rzucie
A) jest bardziej prawdopodobne, że wypadnie reszka.
B) na pewno wypadnie reszka.
C) jest tak samo prawdopodobne, że wypadnie orzeł lub reszka.
D) jest bardziej prawdopodobne, że wypadnie orzeł.
Uczniowie na zimowisku zostali podzielni na 4 grupy. Tabela zawiera informację o liczbie uczniów w poszczególnych grupach z podziałem ze względu na ich wiek.
| Wiek | Grupa I | Grupa II | Grupa III | Grupa IV |
| 10 lat | 20 | 10 | 30 | 20 |
| 11 lat | 30 | 10 | 20 | 0 |
| 12 lat | 40 | 30 | 30 | 20 |
Prawdopodobieństwo, że losowo wybrany uczeń grupy ma 12 lat jest największe, gdy ucznia losujemy z grupy
A) I B) II C) III D) IV
Uczniowie na zimowisku zostali podzielni na 4 grupy. Tabela zawiera informację o liczbie uczniów w poszczególnych grupach z podziałem ze względu na ich wiek.
| Wiek | Grupa I | Grupa II | Grupa III | Grupa IV |
| 10 lat | 20 | 10 | 30 | 20 |
| 11 lat | 30 | 10 | 20 | 0 |
| 12 lat | 40 | 30 | 30 | 20 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo, że losowo wybrany uczeń grupy ma 12 lat jest największe, gdy ucznia losujemy z grupy II. | P | F |
| Prawdopodobieństwo, że losowo wybrany uczeń grupy ma mniej niż 12 lat jest najmniejsze, gdy ucznia losujemy z grupy II. | P | F |
Ze zbioru liczb naturalnych dwucyfrowych nie większych niż 35 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 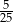 B)
B) 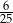 C)
C) 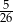 D)
D) 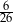
Ze zbioru kolejnych liczb naturalnych 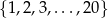 losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
A) 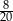 B)
B) 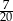 C)
C) 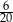 D)
D) 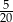
Ze zbioru liczb 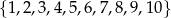 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 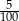 C)
C) 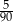 D)
D) 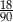
Ze zbioru liczb 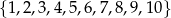 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Organizatorzy loterii fantowej przygotowali zestaw losów, w którym były dwa rodzaje losów: niebieskie i zielone. Losów niebieskich było dwa razy mniej niż losów zielonych i upoważniały one do odbioru cenniejszej nagrody. Uczestnicy loterii losowali po jednym losie, który po wylosowaniu był usuwany z zestawu. Pierwszy uczestnik loterii wyciągnął los niebieski, a drugi uczestnik wyciągnął los zielony.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez trzecią osobę losu niebieskiego jest równe 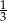 . . | P | F |
Prawdopodobieństwo wyciągnięcia przez pierwszą osobę losu zielonego było równe  . . | P | F |
W szufladzie jest 7 par skarpetek białych i 3 pary skarpetek czarnych. Tomek losuje z szuflady po jednej skarpetce i kładzie ją na stół.
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania czarnej skarpetki jest równe 0,3. | P | F |
| Tomek za pierwszym razem nie wylosował czarnej skarpetki. Prawdopodobieństwo, że za drugim razem wylosuje czarną skarpetkę jest większe. | P | F |
W szufladzie znajduje się 10 par skarpetek, w tym 3 pary skarpetek czarnych. Tomek losowo wyjmuje po jednej skarpetce z szuflady.
Wybierz P, jeśli zdanie jest prawdziwe, lub F jeśli jest fałszywe.
| Tomek, aby mieć pewność, że przynajmniej dwie wyjęte skarpetki będą czarne, musi wyjąć co najmniej 16 skarpetek. | P | F |
| Tomek za pierwszym razem nie wyjął czarnej skarpetki. Prawdopodobieństwo, że za drugim razem wyjmie czarną skarpetkę, wzrosło. | P | F |
W pudełku było 20 kul białych i 10 czarnych. Dołożono jeszcze 10 kul białych i 15 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
W pudełku znajduje się 6 losów, wśród których są 2 losy wygrywające.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu wygrywającego jest dwukrotnie mniejsze, niż wyciągnięcia losu przegrywającego. | P | F |
| Jeśli do pudełka włożymy dodatkowy los wygrywający, to prawdopodobieństwo wygranej wzrośnie. | P | F |
W pudełku było 15 kul białych i 5 czarnych. Dołożono jeszcze 10 kul białych i 20 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
W pudełku jest 30 kul białych i 20 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli 10 kul białych zostanie zastąpionych kulami czarnymi, to prawdopodobieństwa wylosowania kuli czarnej i białej będą równe. | P | F |
| Jeżeli podwoimy liczbę kul czarnych w pudełku, to prawdopodobieństwo wylosowania kuli czarnej wzrośnie dwukrotnie. | P | F |
Do pudełka włożono piłki zielone i czerwone. Wszystkich piłek jest 8, a piłek czerwonych jest 6.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia czerwonej piłki jest trzy razy większe, niż prawdopodobieństwo wyciągnięcia piłki zielonej. | P | F |
| Jeśli z pudełka zabierzemy 2 czerwone piłki, to prawdopodobieństwa wyciągnięcia piłki czerwonej i zielonej będą równe. | P | F |
W pudełku znajduje się 18 losów, wśród których są 2 losy wygrywające.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu przegrywającego jest dziewięciokrotnie większe, niż wyciągnięcia losu wygrywającego. | P | F |
| Jeżeli do pudełka włożymy dwa losy wygrywające to prawdopodobieństwo wygranej wzrośnie o 100%. | P | F |
W kapeluszu znajdują się króliki białe i szare. Królików szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe  . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
A) 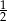 B)
B) 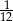 C)
C) 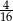 D)
D) 
W woreczku znajdują się piłki białe i szare. Piłek szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z woreczka piłki białej jest równe 0,25. Zatem prawdopodobieństwo wyciągnięcia z woreczka piłki szarej jest równe
A) 0,75 B) 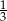 C) 0,25 D) 0,8
C) 0,25 D) 0,8
W kapeluszu znajdują się króliki białe i szare. Prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe 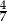 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
A)  B) 0,75 C)
B) 0,75 C)  D)
D) 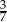
W pudełku znajduje się 30 losów loterii. 5 z tych losów jest wygrywających, 10 jest przegrywających, a wyciągnięcie jednego z pozostałych upoważnia do wyciągnięcia jeszcze jednego losu. Po wyciągnięciu los nie jest zwracany do pudełka. Pierwsza osoba, która brała udział w tej loterii, wyciągnęła los przegrywający.
Czy podane zdania są prawdziwe (P), czy fałszywe (F)?
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu wygrywającego wzrosło. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu przegrywającego zmalało. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu upoważniającego do ponownego losowania nie zmieniło się. | P | F |
Ze zbioru liczb 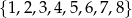 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 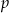 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 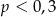 B)
B) 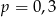 C)
C) 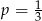 D)
D) 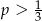
Ze zbioru 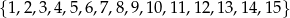 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 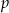 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
A) 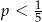 B)
B) 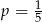 C)
C) 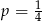 D)
D) 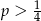
Ze zbioru liczb 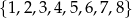 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 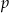 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 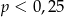 B)
B) 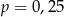 C)
C) 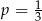 D)
D) 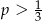
Ze zbioru liczb 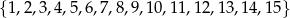 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 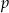 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 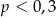 B)
B) 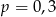 C)
C) 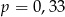 D)
D) 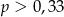
Ze zbioru liczb 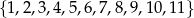 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 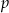 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 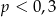 B)
B) 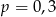 C)
C) 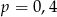 D)
D) 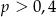
Pewnego dnia w klasie liczącej 11 dziewcząt i 15 chłopców nieobecny był jeden chłopiec i jedna dziewczynka. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 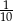 B)
B) 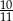 C)
C) 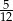 D)
D) 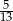
Pewnego dnia w klasie liczącej 16 dziewcząt i 12 chłopców nieobecnych było dwóch chłopców i trzy dziewczynki. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 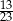 B)
B) 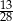 C)
C) 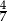 D)
D) 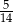
Na rysunku przedstawiono liczbę i rodzaj kul umieszczonych w każdym z czterech pudełek. Z każdego pudełka losujemy jedną kulę.
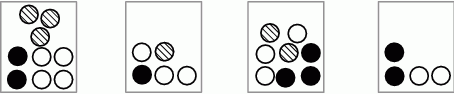
Prawdopodobieństwo wylosowania białej kuli jest największe, gdy kulę losujemy z pudełka
A) 1 B) 2 C) 3 D) 4
W tabeli przedstawiono liczbę i rodzaj kul umieszczonych w czterech pudełkach. Z każdego pudełka losujemy jedną kulę.
| Liczba kul zielonych | Liczba kul niebieskich | Liczba kul czerwonych | |
| Pudełko nr 1 | 4 | 8 | 5 |
| Pudełko nr 2 | 7 | 16 | 9 |
| Pudełko nr 3 | 2 | 7 | 3 |
| Pudełko nr 4 | 7 | 12 | 5 |
Prawdopodobieństwo wylosowania niebieskiej kuli jest największe, gdy kulę losujemy z pudełka nr
A) 1 B) 2 C) 3 D) 4
Ze zbioru dwudziestu czterech kolejnych liczb naturalnych od 1 do 24 losujemy jedną liczbę. Niech 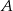 oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 24. Wtedy prawdopodobieństwo zdarzenia
oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 24. Wtedy prawdopodobieństwo zdarzenia 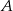 jest równe
jest równe
A) 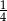 B)
B) 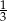 C)
C) 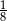 D)
D) 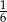
Ze zbioru trzydziestu kolejnych liczb naturalnych od 1 do 30 losujemy jedną liczbę. Niech 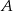 oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia
oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia 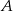 jest równe
jest równe
A) 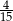 B)
B) 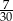 C)
C) 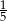 D)
D) 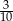
Organizatorzy konkursu matematycznego przygotowali zestaw, w którym było 10 pytań z algebry i 8 pytań z geometrii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z algebry.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z algebry jest równe 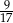 . . | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z geometrii się nie zmieniło. | P | F |
Organizatorzy konkursu z języka polskiego przygotowali zestaw, w którym było 15 pytań z gramatyki i 7 pytań z ortografii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z gramatyki.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z ortografii zwiększyło się. | P | F |
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z gramatyki jest równe 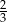 . . | P | F |
W pudełku znajduje się 14 par skarpetek, w tym 8 par skarpetek czerwonych i 6 par skarpetek niebieskich. Ania losowo wybiera z pojemnika 14 skarpetek. Prawdopodobieństwo, że Ania wybrała co najmniej dwie skarpetki czerwone jest równe
A) 1 B) 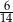 C)
C) 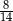 D)
D) 
Doświadczenie losowe polega na dwukrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 1, a jeśli reszka – zapisujemy 2. Wynikiem doświadczenia jest zapisana liczba dwucyfrowa. Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 3?
A) 0 B) 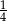 C)
C) 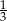 D)
D) 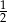
Doświadczenie losowe polega na dwukrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 6, a jeśli reszka – zapisujemy 4. Wynikiem doświadczenia jest zapisana liczba dwucyfrowa. Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 3?
A) 0 B) 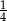 C)
C) 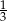 D)
D)