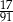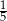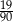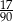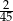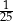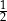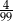Do dwóch koszy wrzucono piłki szare i czarne. Na diagramie przedstawiono liczbę piłek każdego koloru w I i w II koszu.
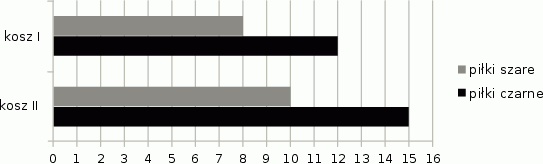
Czy wylosowanie piłki czarnej z kosza II jest bardziej prawdopodobne niż wylosowanie piłki czarnej z kosza I? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A. | w koszu II jest więcej piłek czarnych niż w koszu I. |
| B. | stosunek liczby piłek czarnych do liczby wszystkich piłek jest taki sam w obu koszach. |
| C. | w koszu II jest o 3 piłki czarne więcej niż w koszu I, ale szarych – tylko o 2 więcej. |

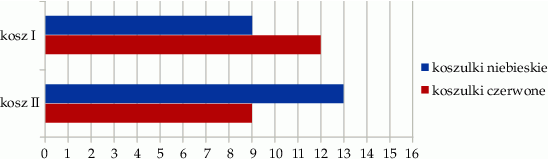
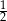 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C. 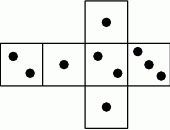
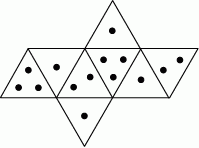
 .
. 
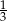 .
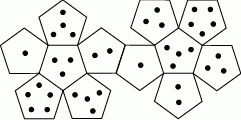
. 
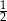 .
. 
 .
.  .
. 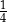 , to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie.
, to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie. 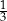
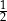

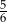
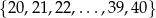 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe 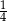
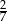
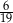
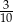
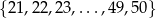 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe 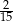

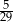
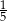


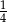
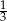


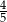

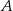 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 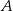 jest równe
jest równe 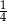
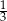
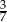

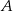 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 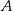 jest równe
jest równe 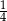
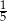
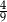
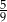
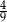

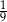
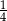
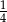
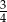
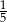

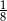
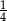


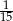
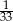
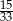
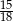
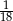
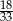
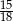
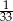
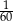
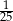
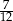
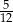
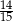
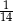
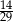
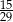

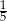
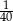
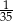
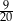
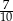
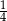
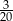
 . Liczba kobiet w tej grupie jest równa
. Liczba kobiet w tej grupie jest równa  jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.  może być równa 35.
może być równa 35.  może być równa 1024.
może być równa 1024.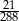 stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe 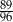
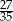
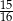
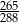
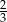 .
. 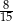
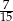
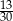
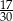
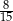
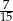
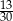
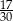
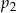 prawdopodobieństwo wyrzucenia liczby podzielnej przez 2, a przez
prawdopodobieństwo wyrzucenia liczby podzielnej przez 2, a przez 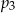 – prawdopodobieństwo wyrzucenia liczby podzielnej przez 3.
– prawdopodobieństwo wyrzucenia liczby podzielnej przez 3.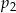 jest mniejsza od liczby
jest mniejsza od liczby 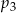 .
.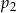 i
i 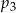 są mniejsze od
są mniejsze od 
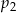 prawdopodobieństwo wyrzucenia liczby parzystej, a przez
prawdopodobieństwo wyrzucenia liczby parzystej, a przez 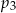 – prawdopodobieństwo wyrzucenia liczby większej od 3.
– prawdopodobieństwo wyrzucenia liczby większej od 3.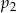 jest większa od liczby
jest większa od liczby 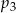 .
.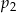 i
i 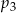 są większe od
są większe od 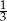
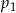 prawdopodobieństwo wyrzucenia liczby pierwszej, a przez
prawdopodobieństwo wyrzucenia liczby pierwszej, a przez 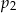 – prawdopodobieństwo wyrzucenia liczby złożonej.
– prawdopodobieństwo wyrzucenia liczby złożonej.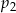 jest mniejsza od liczby
jest mniejsza od liczby 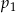 .
.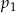 i
i 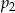 są mniejsze od
są mniejsze od 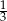 .
. 
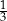
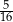
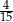

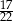
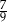
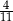
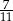
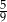 . W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 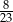 .
. 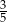 .
. 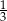
 .
.