Objętość i pole/Sześcian - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Sześcian/Objętość i pole

Po wydłużeniu każdej krawędzi sześcianu o 2, długość jego przekątnej podwoiła się. Oblicz pole powierzchni całkowitej powiększonego sześcianu.

Odległość wierzchołka sześcianu od przekątnej sześcianu (do której dany wierzchołek nie należy) jest równa 4 cm. Oblicz objętość sześcianu.

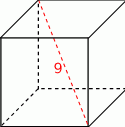
Przekątna sześcianu ma długość 9. Oblicz pole powierzchni całkowitej tego sześcianu.

Przekątna sześcianu jest o 3 dłuższa od krawędzi sześcianu. Oblicz objętość tego sześcianu.

Ukryj Podobne zadania

Długość krawędzi sześcianu jest o 2 krótsza od długości jego przekątnej. Oblicz długość przekątnej tego sześcianu.

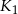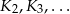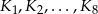Niech będzie sześcianem o krawędzi długości . Konstruujemy kolejno sześciany K2,K 3,... takie, że pole powierzchni całkowitej kolejnego sześcianu jest dwa razy większe od pola powierzchni poprzedniego sześcianu. Oblicz sumę objętości sześcianów K ,K ,...,K 1 2 8 .

Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 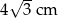√ -- 4 3 cm .

Krawędź sześcianu jest o 4 krótsza od jego przekątnej. Oblicz pole powierzchni całkowitej tego sześcianu.

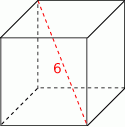
Przekątna sześcianu ma długość 6. Oblicz objętość tego sześcianu.

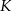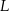Punkty i są środkami odpowiednio podstawy 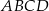ABCD i krawędzi 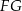F G sześcianu 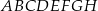ABCDEF GH . Suma kwadratów długości odcinków 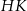i 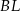jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.

Ukryj Podobne zadania

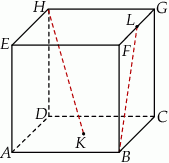
Punkty 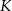i 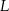są środkami odpowiednio podstawy 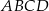ABCD i krawędzi 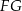F G sześcianu 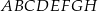ABCDEF GH . Suma kwadratów długości odcinków 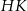i 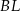jest równa 44. Oblicz objętość tego sześcianu.

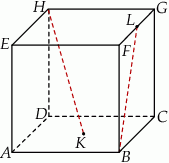
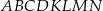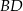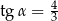Sześcian ABCDKLMN przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem takim, że tg α = 43 (zobacz rysunek).

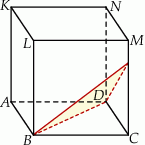
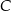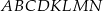Odległość wierzchołka od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu ABCDKLMN .