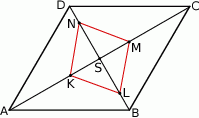
Na bokach  i
i  rombu
rombu  wybrano odpowiednio punkty
wybrano odpowiednio punkty 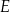 i
i 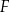 tak, że
tak, że 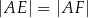 . Pole pięciokąta
. Pole pięciokąta 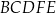 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 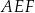 . Punkt
. Punkt 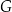 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 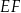 i przekątnej
i przekątnej 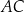 . Oblicz Oblicz
. Oblicz Oblicz 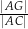 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na bokach 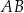 i
i 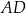 rombu
rombu 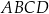 wybrano odpowiednio punkty
wybrano odpowiednio punkty  i
i  tak, że
tak, że 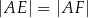 . Pole pięciokąta
. Pole pięciokąta 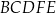 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 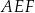 . Punkt
. Punkt 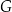 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 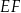 i przekątnej
i przekątnej 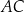 . Oblicz Oblicz
. Oblicz Oblicz 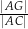 .
.

Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.
O ile procent zmniejszy się pole rombu, jeśli jedną przekątną rombu zwiększymy o 20%, a drugą przekątną skrócimy o 40%?
Bok rombu 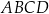 ma długość
ma długość  , a sinus jego kąta ostrego
, a sinus jego kąta ostrego 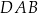 jest równy
jest równy 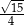 . Na bokach
. Na bokach 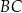 i
i 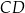 wybrano punkty
wybrano punkty 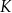 i
i 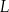 odpowiednio tak, że odcinki
odpowiednio tak, że odcinki 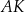 i
i 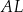 podzieliły pole rombu
podzieliły pole rombu 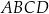 na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).
Oblicz długość odcinka  .
.
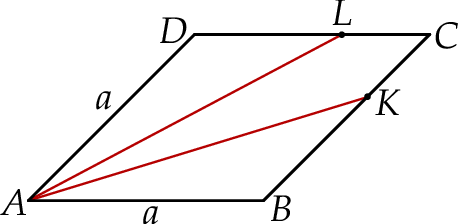
Na bokach  i
i  rombu
rombu 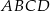 wybrano punkty
wybrano punkty 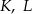 i
i 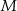 w ten sposób, że
w ten sposób, że 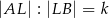 oraz
oraz 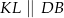 ,
, 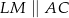 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 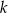 , dla których pole pięciokąta
, dla których pole pięciokąta 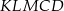 stanowi
stanowi 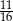 pola rombu.
pola rombu.
Oblicz pole rombu, którego jeden z kątów wewnętrznych wynosi 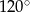 , a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
, a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
Krótsza przekątna rombu o długości 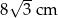 dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
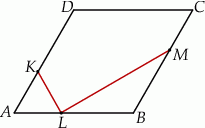
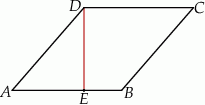
Wysokość 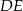 rombu
rombu 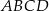 dzieli bok
dzieli bok 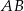 tego rombu tak, że
tego rombu tak, że 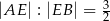 (zobacz rysunek).
(zobacz rysunek).
Oblicz wartość wyrażenia
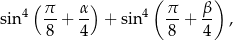
gdzie  i
i 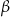 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu 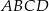 .
.
Na bokach 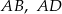 i
i 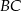 rombu
rombu 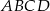 wybrano odpowiednio punkty
wybrano odpowiednio punkty 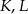 i
i 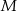 w ten sposób, że odcinki
w ten sposób, że odcinki 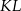 i
i 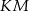 są równoległe do przekątnych rombu. Wykaż, że odcinek
są równoległe do przekątnych rombu. Wykaż, że odcinek 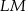 przechodzi przez punkt przecięcia przekątnych rombu.
przechodzi przez punkt przecięcia przekątnych rombu.
Oblicz pole rombu, w którym długość boku jest równa 13 cm, a długości przekątnych różnią się o 14 cm.
Oblicz pole rombu o obwodzie 68 cm, w którym długości przekątnych różnią się o 14 cm.
Obwód rombu jest równy 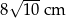 , a jedna z jego przekątnych jest o 8 cm dłuższa od drugiej. Oblicz pole rombu.
, a jedna z jego przekątnych jest o 8 cm dłuższa od drugiej. Oblicz pole rombu.
Dany jest romb o boku długości 35. Długości przekątnych tego rombu różnią się o 14. Oblicz pole tego rombu.
Na kole opisany jest romb. Stosunek pola koła do pola powierzchni rombu wynosi 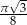 . Wyznacz miarę kąta ostrego rombu.
. Wyznacz miarę kąta ostrego rombu.
W romb o boku długości 10 cm i wysokości 8 cm wpisano okrąg  .
.
 i wyznacz długość promienia tego okręgu.
i wyznacz długość promienia tego okręgu. 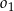 i
i 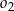 w skali 1:2.
w skali 1:2.Kąt ostry rombu  ma miarę
ma miarę 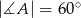 . Na bokach
. Na bokach 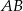 i
i 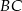 wybrano punkty
wybrano punkty 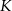 i
i 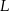 w ten sposób, że
w ten sposób, że 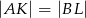 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 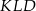 jest trójkątem równobocznym.
jest trójkątem równobocznym.
Bok rombu ma długość 13, suma długości przekątnych jest równa 34.
Długość boku rombu jest równa  , a długości jego przekątnych są równe
, a długości jego przekątnych są równe 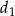 i
i 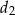 . Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że
. Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że 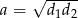 .
.
Długość boku rombu 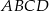 jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
Obwód rombu wynosi 68 cm, a długość jednej z jego przekątnych stanowi 187,5% długości drugiej przekątnej. Oblicz pole tego rombu.
Bok rombu 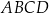 ma długość
ma długość  , a kąt ostry przy wierzchołku
, a kąt ostry przy wierzchołku 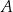 ma miarę
ma miarę 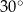 . Oblicz długość odcinka łączącego wierzchołek
. Oblicz długość odcinka łączącego wierzchołek 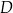 rombu z punktem boku
rombu z punktem boku 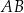 , dzielącego ten bok w stosunku
, dzielącego ten bok w stosunku 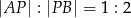 .
.
Na bokach 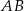 i
i 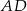 rombu
rombu 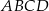 wybrano odpowiednio punkty
wybrano odpowiednio punkty 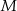 i
i 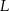 w ten sposób, że
w ten sposób, że 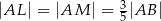 . Odcinek
. Odcinek 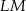 jest styczny do okręgu wpisanego w romb
jest styczny do okręgu wpisanego w romb 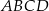 . Punkt
. Punkt 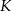 jest punktem styczności okręgu wpisanego w ten romb z bokiem
jest punktem styczności okręgu wpisanego w ten romb z bokiem 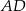 (zobacz rysunek).
(zobacz rysunek).
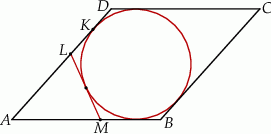
Wykaż, że 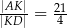 .
.
Znaleźć kąt ostry rombu, jeżeli wiadomo, że jego pole jest równe 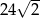 , a promień okręgu w niego wpisanego równy
, a promień okręgu w niego wpisanego równy 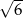 .
.
Na bokach 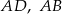 i
i 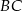 rombu
rombu 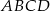 wybrano punkty
wybrano punkty 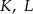 i
i 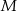 w ten sposób, że
w ten sposób, że 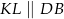 i
i 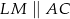 . Uzasadnij, że pole czworokąta
. Uzasadnij, że pole czworokąta 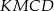 stanowi połowę pola rombu.
stanowi połowę pola rombu.
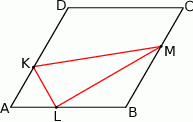
Przekątne rombu 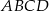 przecinają się w punkcie
przecinają się w punkcie 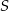 . Punkty
. Punkty 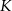 i
i 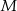 leżą na przekątnej
leżą na przekątnej 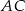 tak, że
tak, że 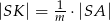 i
i 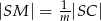 . Punkty
. Punkty 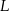 i
i 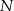 leżą na przekątnej
leżą na przekątnej 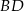 tak, że
tak, że 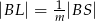 i
i 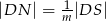 (zobacz rysunek). Wykaż, że jeżeli stosunek pola czworokąta
(zobacz rysunek). Wykaż, że jeżeli stosunek pola czworokąta 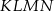 do pola rombu
do pola rombu 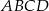 jest równy 1:4, to
jest równy 1:4, to 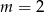 .
.