Wykres funkcji 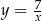 przesunięto o wektor
przesunięto o wektor ![→ v = [− 3,k]](https://img.zadania.info/zad/2263710/HzadT1x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 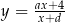 . Wyznacz
. Wyznacz 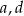 i
i 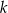 .
.
/Szkoła średnia/Funkcje - wykresy/Homografia/Przesunięcie wykresu
Wykres funkcji 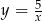 przesunięto o wektor
przesunięto o wektor ![→ v = [2,k]](https://img.zadania.info/zad/9133400/HzadT1x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 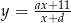 . Wyznacz
. Wyznacz 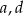 i
i 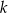 .
.
Wykres funkcji 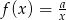 dla
dla 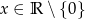 , gdzie
, gdzie 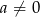 , przesunięto o wektor
, przesunięto o wektor ![→u = [− 3,2]](https://img.zadania.info/zad/2875082/HzadT3x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 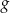 . Do wykresu funkcji
. Do wykresu funkcji 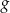 należy punkt
należy punkt 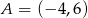 . Oblicz
. Oblicz  , następnie rozwiąż nierówność
, następnie rozwiąż nierówność 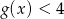 .
.
Wykres funkcji 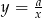 , gdzie
, gdzie 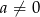 przesunięto o wektor
przesunięto o wektor ![[2,3]](https://img.zadania.info/zad/5074509/HzadT2x.gif) i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu
i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu 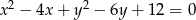 . Wyznacz
. Wyznacz  .
.
Dana jest funkcja 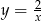 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→u = [1,− 5]](https://img.zadania.info/zad/5948271/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Dana jest funkcja 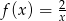 . Narysuj wykres i wyznacz przedziały monotoniczności funkcji
. Narysuj wykres i wyznacz przedziały monotoniczności funkcji 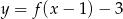 .
.
Wykres funkcji 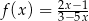 przesunięto o wektor
przesunięto o wektor ![[− 3,2]](https://img.zadania.info/zad/7906055/HzadT1x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 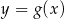 . Oblicz granicę
. Oblicz granicę
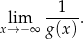
Na rysunku przedstawiony jest wykres funkcji 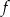 określonej wzorem
określonej wzorem 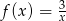 dla
dla 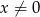 .
.
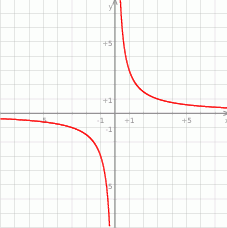
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 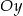 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 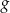 o wzorze
o wzorze 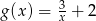 dla
dla 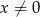 .
.
- Narysuj wykres funkcji
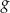 .
. - Oblicz największą wartość funkcji
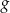 w przedziale
w przedziale 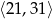 .
. - Podaj, o ile jednostek wzdłuż osi
 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 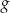 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.

