Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 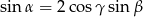 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.
/Konkursy/Zadania/Geometria
Wysokość trójkąta prostokątnego poprowadzona do przeciwprostokątnej ma długość 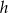 i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.
i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.
Odległość między środkami okręgów o promieniach 2 i 7 wynosi 13. Prosta 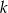 jest styczna do obu okręgów w punktach
jest styczna do obu okręgów w punktach 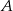 i
i 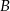 . Oblicz długość odcinka
. Oblicz długość odcinka 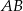 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
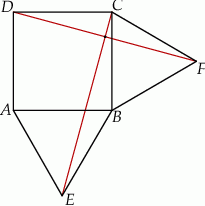
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
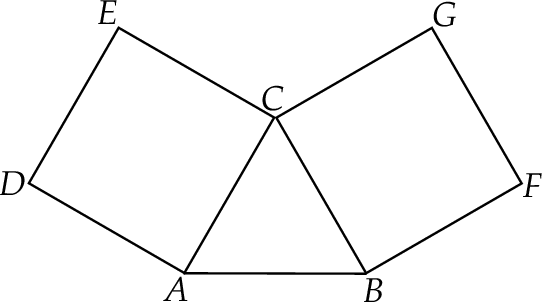
Wykaż, że punkty 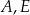 i
i 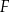 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Na bokach 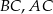 i
i 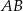 trójkąta
trójkąta 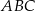 wybrano odpowiednio punkty
wybrano odpowiednio punkty 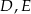 i
i 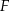 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 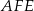 i
i 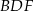 są styczne, to punkt
są styczne, to punkt 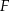 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 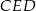 .
.
Ramiona kąta ostrego o mierze 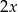 przecięto prostą
przecięto prostą 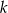 prostopadłą do dwusiecznej kąta, która jest odległa o
prostopadłą do dwusiecznej kąta, która jest odległa o 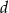 od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej
od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 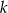 . Oblicz odległość środków tych okręgów.
. Oblicz odległość środków tych okręgów.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4. Jakie pole ma koło opisane na tym kwadracie?
Czworokąty 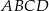 i
i 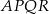 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 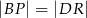 .
.
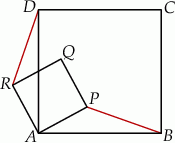
- Uzasadnij, że suma skierowanych kątów zewnętrznych dowolnego wielokąta (niekoniecznie wypukłego) jest równa
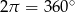 .
. - Uzasadnij, że suma nieskierowanych kątów zewnętrznych dowolnego wielokąta wypukłego jest równa
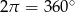 .
. - Wyprowadź wzór na sumę kątów wewnętrznych dowolnego
 –kąta.
–kąta.
Pole trapezu jest równe 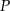 , a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
, a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
Punkt 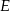 leży na ramieniu
leży na ramieniu 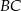 trapezu
trapezu 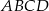 , w którym
, w którym 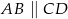 . Udowodnij, że
. Udowodnij, że 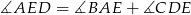 .
.
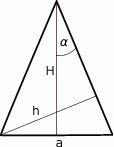
W trójkącie równoramiennym (patrz rysunek) długość podstawy wynosi  , zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe
, zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe 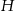 i
i 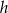 . Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę
. Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę  .
.
- Wyraź
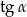 w zależności od wielkości
w zależności od wielkości  i
i 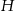 .
. - Wyraź
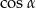 w zależności od wielkości
w zależności od wielkości  i
i 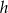 .
. - Wykaż, że jeśli
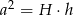 , to
, to 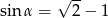 .
.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.
Do dwóch okręgów przecinających się w punktach 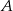 i
i 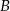 poprowadzono wspólną styczną
poprowadzono wspólną styczną 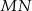 , przy czym punkt
, przy czym punkt 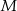 należy do pierwszego, a punkt
należy do pierwszego, a punkt 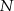 do drugiego okręgu. Wykaż, że prosta
do drugiego okręgu. Wykaż, że prosta 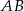 dzieli odcinek
dzieli odcinek 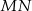 na połowy.
na połowy.
W trójkącie 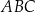 kąt
kąt 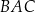 jest dwa razy większy od kąta
jest dwa razy większy od kąta 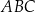 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 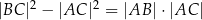 .
.
Dany jest trójkąt 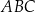 , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta 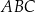 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 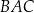 . Wykaż, że długości boków tego trójkąta spełniają warunek
. Wykaż, że długości boków tego trójkąta spełniają warunek
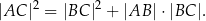
Średnica 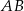 i cięciwa
i cięciwa 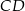 okręgu o środku
okręgu o środku 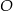 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 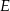 takim, że
takim, że 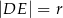 . Wykaż, że
. Wykaż, że 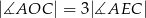 .
.
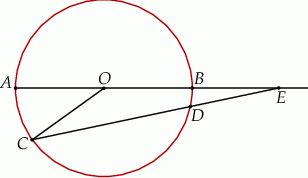
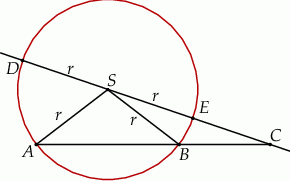
Dany jest okrąg o środku w punkcie 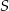 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 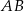 poza punkt
poza punkt 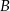 odłożono odcinek
odłożono odcinek 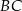 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 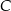 i
i 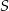 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 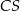 przecina dany okrąg w punktach
przecina dany okrąg w punktach 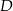 i
i 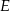 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 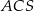 jest równa
jest równa  , to miara kąta
, to miara kąta 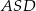 jest równa
jest równa  .
.
Punkt 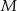 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 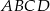 . Punkt
. Punkt 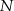 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 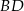 i wysokości
i wysokości 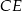 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 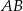 . Wykaż, że
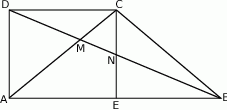
. Wykaż, że 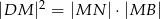 .
.
Okrąg wpisany w trójkąt 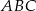 jest styczny do boków
jest styczny do boków 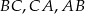 odpowiednio w punktach
odpowiednio w punktach 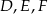 . Punkty
. Punkty 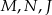 są odpo- wiednio środkami okręgów wpisanych w trójkąty
są odpo- wiednio środkami okręgów wpisanych w trójkąty 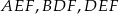 . Dowieść, że punkty
. Dowieść, że punkty 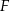 i
i 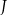 są symetryczne względem prostej
są symetryczne względem prostej 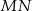 .
.
Na zewnątrz kwadratu 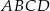 na bokach
na bokach 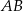 i
i 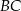 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 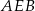 i
i 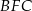 . Uzasadnij, że proste
. Uzasadnij, że proste 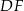 i
i  są prostopadłe.
są prostopadłe.
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.

