Ramiona trapezu są średnicami dwóch okręgów. Wykaż, że jeśli okręgi te są styczne zewnętrznie, to w trapez ten można wpisać okrąg.
/Konkursy/Zadania/Geometria
Pole przekroju ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i równoległą do krawędzi bocznej rozłącznej z tą przekątną wynosi  . Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
. Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
Punkt  leży na boku
leży na boku  trójkąta równoramiennego
trójkąta równoramiennego  , w którym
, w którym 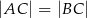 .
.
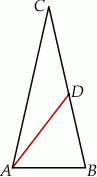
Odcinek 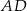 dzieli trójkąt
dzieli trójkąt 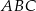 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 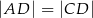 oraz
oraz 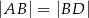 . Udowodnij, że
. Udowodnij, że 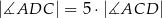 .
.
Punkt 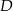 leży na boku
leży na boku 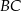 trójkąta równoramiennego, w którym
trójkąta równoramiennego, w którym 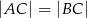 . Odcinek
. Odcinek 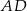 dzieli trójkąt
dzieli trójkąt 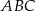 na dwa trójkąty równoramienne takie, że
na dwa trójkąty równoramienne takie, że 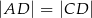 i
i 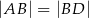 . Wykaż, że
. Wykaż, że 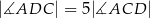 .
.
Kąty w trójkącie mają miary: 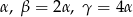 . Wykaż, że długości boków
. Wykaż, że długości boków 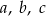 tego trójkąta spełniają równość:
tego trójkąta spełniają równość: 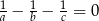 .
.
Na bokach trójkąta równobocznego 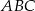 (na zewnątrz tego trójkąta) zbudowano kwadraty
(na zewnątrz tego trójkąta) zbudowano kwadraty 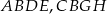 i
i 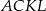 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 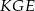 jest równoboczny.
jest równoboczny.
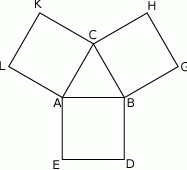
Dwa okręgi są styczne zewnętrznie w punkcie  . Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach
. Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach 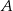 i
i 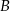 (
(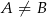 ). Wykaż, że kąt
). Wykaż, że kąt 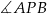 jest prosty.
jest prosty.
Dwa okręgi są zewnętrznie styczne w punkcie 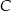 oraz są styczne do prostej
oraz są styczne do prostej 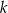 w punktach
w punktach 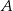 i
i 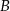 odpowiednio (zobacz rysunek).
odpowiednio (zobacz rysunek).
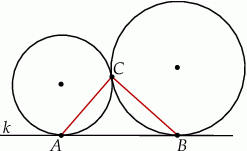
Uzasadnij, że trójkąt 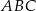 jest prostokątny.
jest prostokątny.
Oblicz jaka może być najmniejsza możliwa długość boku 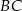 trójkąta
trójkąta 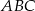 jeżeli
jeżeli 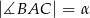 i pole trójkąta
i pole trójkąta 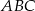 jest równe
jest równe 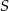 .
.
Przekątna 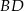 rombu
rombu 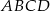 przecina jego wysokość
przecina jego wysokość 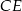 , poprowadzoną na bok
, poprowadzoną na bok 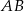 , w punkcie
, w punkcie 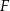 . Oblicz pole rombu
. Oblicz pole rombu 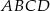 , jeśli wiadomo, że
, jeśli wiadomo, że 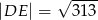 oraz
oraz 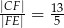 .
.
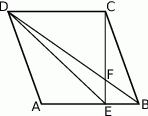
Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Trapez równoramienny 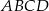 o podstawach
o podstawach 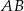 i
i 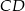 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 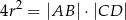 .
.
W trójkacie 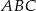 dwusieczna kąta
dwusieczna kąta 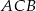 przecina bok
przecina bok 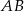 w punkcie
w punkcie 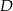 . Długosci boków
. Długosci boków 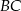 i
i 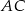 są równe odpowiednio
są równe odpowiednio  i
i 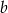 , a długość odcinka
, a długość odcinka 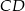 jest równa
jest równa 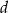 . Wykaż, że
. Wykaż, że 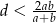 .
.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4 cm.
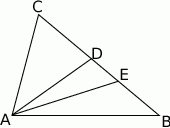
Na boku 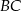 trójkąta
trójkąta 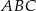 wybrano punkt
wybrano punkt 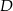 tak, by
tak, by 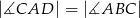 . Odcinek
. Odcinek 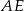 jest dwusieczną kąta
jest dwusieczną kąta 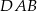 . Udowodnij, że
. Udowodnij, że 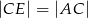 .
.
W trójkącie 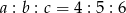 . Wykaż, że w tym trójkącie
. Wykaż, że w tym trójkącie 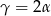 .
.
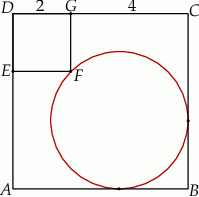
Na rysunku przedstawiono dwa kwadraty: 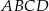 i
i 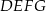 , przy czym punkty
, przy czym punkty 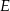 i
i 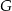 należą do odcinków
należą do odcinków 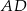 i
i 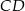 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 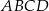 i przechodzi przez punkt
i przechodzi przez punkt 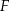 . Wykaż, że jeżeli
. Wykaż, że jeżeli 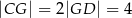 , to promień okręgu jest równy
, to promień okręgu jest równy 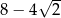 .
.
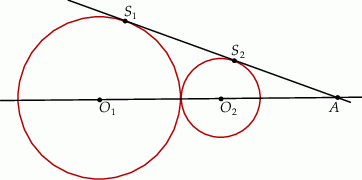
Dane są 2 koła styczne zewnętrznie o promieniach  i
i  (
(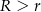 ) oraz środkach
) oraz środkach 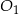 i
i 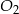 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 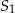 i
i 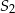 odpowiednio (
odpowiednio (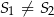 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 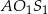 , gdzie
, gdzie 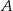 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 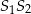 i
i 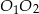 .
.
Podstawy trapezu 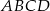 mają długości
mają długości 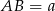 i
i 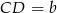 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 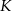 i
i 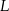 w ten sposób, że odcinek
w ten sposób, że odcinek 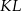 jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka
jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka 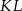 .
.
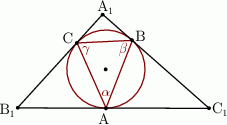
Boki trójkąta 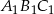 są styczne do okręgu w punktach
są styczne do okręgu w punktach 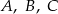 , a kąty trójkąta
, a kąty trójkąta 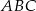 są odpowiednio równe
są odpowiednio równe 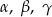 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 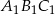 .
.
Przedłużenia przeciwległych boków czworokąta wpisanego w okrąg tworzą kąty ostre o miarach 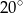 i
i 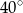 . Oblicz miary kątów czworokąta.
. Oblicz miary kątów czworokąta.
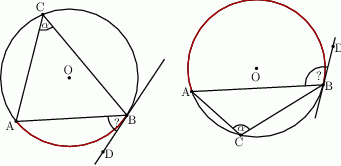
Prosta 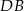 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 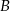 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 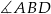 jeśli
jeśli 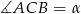 .
.