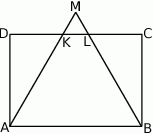
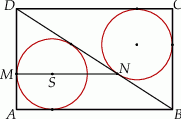
Dany jest prostokąt  . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt  jest styczny do przekątnej
jest styczny do przekątnej  w punkcie
w punkcie 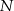 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 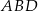 jest styczny do boku
jest styczny do boku 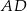 w punkcie
w punkcie 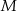 , a środek
, a środek 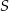 tego okręgu leży na odcinku
tego okręgu leży na odcinku 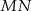 , jak na rysunku.
, jak na rysunku.
Wykaż, że 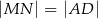 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest prostokąt 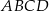 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 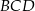 jest styczny do przekątnej
jest styczny do przekątnej 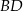 w punkcie
w punkcie 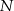 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 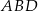 jest styczny do boku
jest styczny do boku 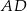 w punkcie
w punkcie 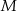 , a środek
, a środek 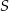 tego okręgu leży na odcinku
tego okręgu leży na odcinku 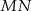 , jak na rysunku.
, jak na rysunku.

Wykaż, że 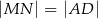 .
.
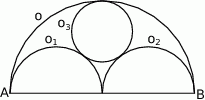
W półkolu  o średnicy
o średnicy 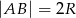 narysowano dwa przystające i zewnętrznie styczne półkola
narysowano dwa przystające i zewnętrznie styczne półkola 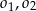 , których środki leżą na odcinku
, których środki leżą na odcinku  , i które są wewnętrznie styczne do półkola
, i które są wewnętrznie styczne do półkola  . Oblicz promień okręgu
. Oblicz promień okręgu  , który jest styczny do
, który jest styczny do  i
i  .
.
W trójkącie prostokątnym 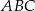 o kącie prostym w wierzchołku
o kącie prostym w wierzchołku 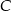 obrano taki punkt
obrano taki punkt 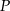 , że pola trójkątów
, że pola trójkątów 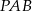 ,
, 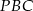 i
i 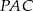 są równe. Oblicz długość odcinka
są równe. Oblicz długość odcinka 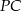 , wiedząc, że
, wiedząc, że 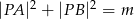 .
.
Wódz indiański wysłał trzech zwiadowców na zachód, północ i wschód. Każdy z nich oddalił się o 5 km od obozu i miał w zasięgu wzroku teren o promieniu 5 km.
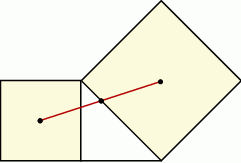
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
W prostokącie 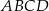 wierzchołek
wierzchołek 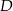 połączono odcinkami ze środkami
połączono odcinkami ze środkami 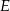 i
i 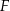 boków
boków 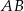 i
i 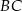 , zaś
, zaś 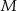 i
i 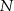 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 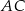 .
.
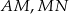 i
i 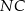 są jednakowej długości.
są jednakowej długości. 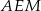 i
i 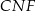 mają równe pola.
mają równe pola.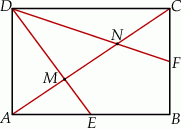
Wykaż, że jeżeli 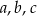 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 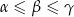 to
to 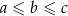 .
.
Każdy kąt trójkąta 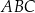 ma miarę mniejszą niż
ma miarę mniejszą niż 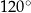 . Udowodnij, że wewnątrz trójkąta
. Udowodnij, że wewnątrz trójkąta 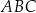 istnieje punkt
istnieje punkt 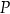 taki, że
taki, że
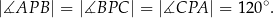
Podstawy trapezu 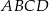 mają długości
mają długości 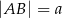 i
i 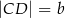 , przy czym
, przy czym 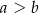 . Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość
. Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość 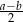 .
.
Oblicz pole rombu 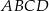 , wiedząc, że długości promieni okręgów opisanych na trójkątach
, wiedząc, że długości promieni okręgów opisanych na trójkątach 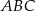 i
i 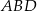 odpowiednio są równe
odpowiednio są równe 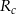 i
i 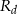 .
.
Przez środek 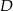 przyprostokątnej
przyprostokątnej 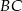 trójkąta prostokątnego
trójkąta prostokątnego 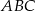 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 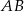 . Prosta ta przecina proste
. Prosta ta przecina proste 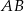 i
i 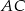 odpowiednio w punktach
odpowiednio w punktach 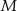 i
i 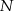 . Wykaż, że
. Wykaż, że 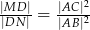 .
.
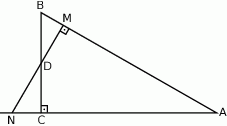
Styczna w punkcie 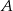 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 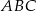 przecina prostą
przecina prostą 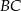 w punkcie
w punkcie 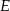 . Niech
. Niech 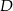 będzie punktem przecięcia dwusiecznej kąta
będzie punktem przecięcia dwusiecznej kąta 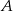 z prostą
z prostą 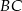 . Udowodnić, że
. Udowodnić, że 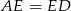 .
.
Na bokach 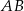 i
i 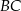 prostokąta
prostokąta 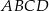 wybrano punkty
wybrano punkty 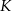 i
i 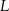 w ten sposób, że trójkąt
w ten sposób, że trójkąt 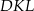 jest ostrokątny oraz
jest ostrokątny oraz 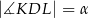 . Odcinek
. Odcinek 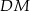 jest wysokością trójkąta
jest wysokością trójkąta 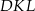 .
.
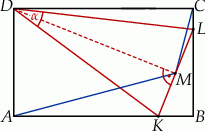
Wykaż, że 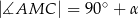 .
.
Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.
Przez każde dwa sąsiednie wierzchołki czworokąta  wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
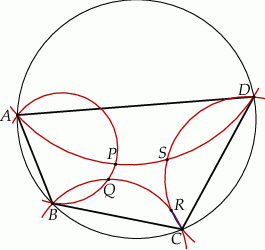
Wykaż, że punkty 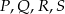 , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
W trójkąt równoboczny wpisane są 3 koła o równych promieniach, przy czym każde koło jest styczne do dwóch boków trójkąta oraz do dwóch pozostałych kół. Oblicz stosunek sumy pól tych kół do pola trójkąta.
W trójkącie 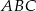 , o bokach długości
, o bokach długości 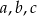 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 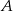 z punktem
z punktem 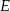 na boku
na boku 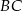 takim, że
takim, że 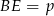 i
i 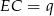 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 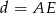 , to
, to 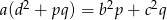 (twierdzenie Stewarta).
(twierdzenie Stewarta).
Punkt 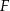 jest środkiem boku
jest środkiem boku 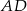 prostokąta
prostokąta 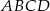 , w którym
, w którym 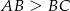 . Punkt
. Punkt 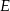 jest takim punktem boku
jest takim punktem boku 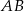 tego prostokąta, że prosta
tego prostokąta, że prosta 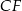 jest dwusieczną kąta
jest dwusieczną kąta 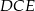 . Wykaż, że trójkąt
. Wykaż, że trójkąt 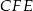 jest prostokątny.
jest prostokątny.
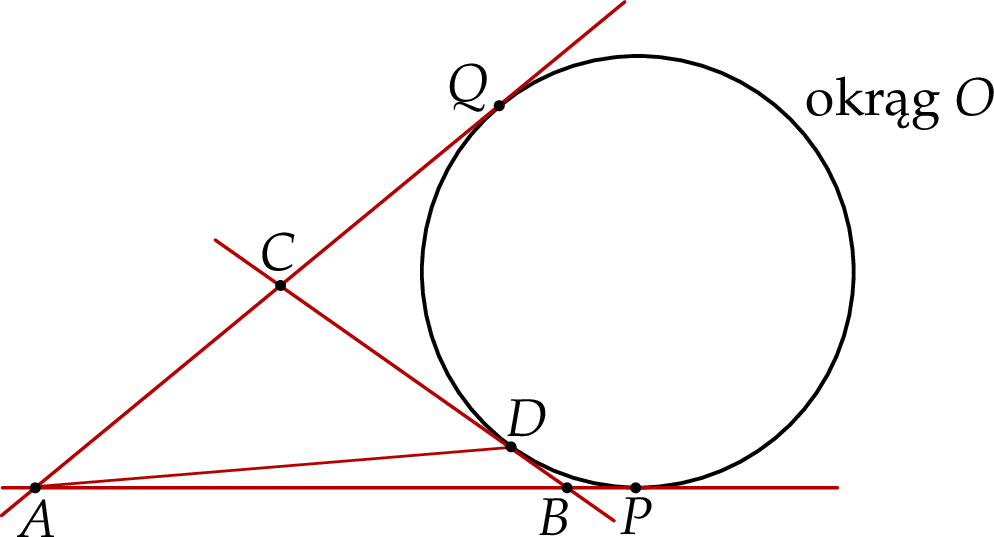
Dany jest okrąg 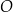 . Przez punkt
. Przez punkt 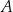 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 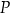 oraz
oraz 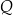 . Przez punkt
. Przez punkt 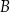 leżący na odcinku
leżący na odcinku 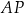 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 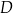 , która przecięła odcinek
, która przecięła odcinek  w punkcie
w punkcie 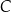 (zobacz rysunek).
(zobacz rysunek).
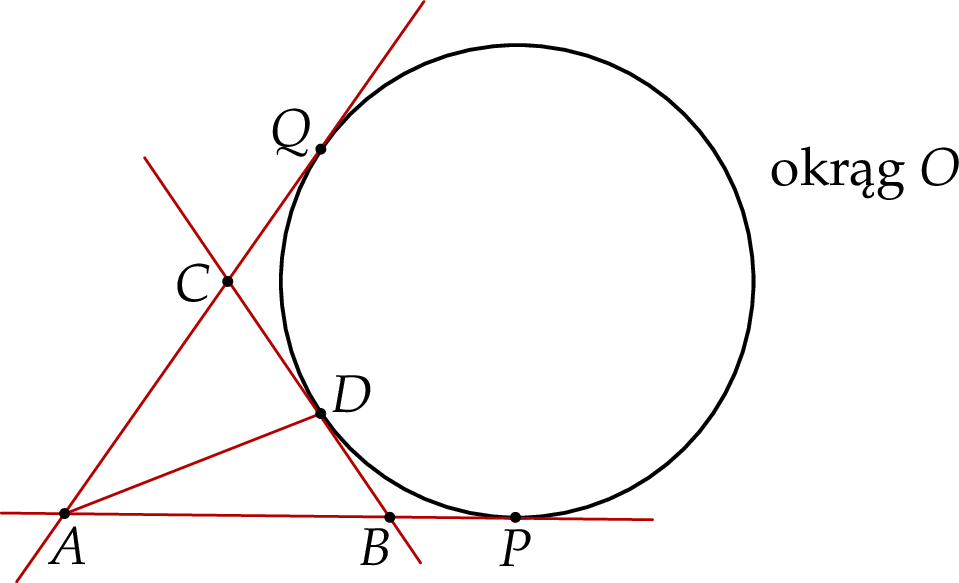
Wykaż, że jeżeli 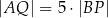 oraz
oraz 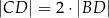 , to trójkąt
, to trójkąt 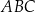 jest równoramienny.
jest równoramienny.
Dany jest okrąg 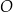 . Przez punkt
. Przez punkt 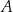 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 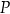 oraz
oraz 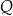 . Przez punkt
. Przez punkt 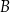 leżący na odcinku
leżący na odcinku 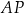 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 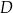 , która przecięła odcinek
, która przecięła odcinek 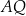 w punkcie
w punkcie 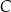 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że jeżeli 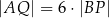 oraz
oraz 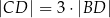 , to trójkąt
, to trójkąt  nie jest równoramienny.
nie jest równoramienny.
Dany jest prostokąt 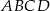 , w którym
, w którym 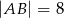 i
i 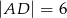 . Na boku
. Na boku 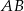 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 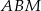 (patrz rysunek). Oblicz obwód trójkąta
(patrz rysunek). Oblicz obwód trójkąta 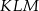 .
.