Funkcja 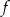 określona jest wzorem
określona jest wzorem 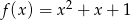 . Znajdź wzór funkcji
. Znajdź wzór funkcji 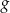 , której wykres otrzymamy:
, której wykres otrzymamy:
- przesuwając wykres funkcji o wektor
![[− 1;− 3]](https://img.zadania.info/zad/2335345/HzadT3x.gif) , a następnie otrzymany wykres przekształcając w symetrii względem osi
, a następnie otrzymany wykres przekształcając w symetrii względem osi 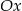 ;
; - dokonując obu przekształceń z poprzedniego punktu, ale w odwrotnej kolejności.

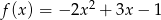 przesunięto o
przesunięto o 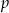 jednostek wzdłuż osi
jednostek wzdłuż osi 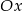 i o
i o 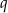 jednostek wzdłuż osi
jednostek wzdłuż osi 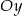 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 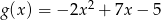 .
. 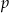 i
i 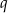 .
. 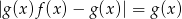 .
.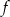 danej wzorem
danej wzorem 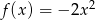 przesunięto wzdłuż osi
przesunięto wzdłuż osi 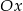 o 3 jednostki w prawo oraz wzdłuż osi
o 3 jednostki w prawo oraz wzdłuż osi 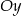 o 8 jednostek w górę, otrzymując wykres funkcji
o 8 jednostek w górę, otrzymując wykres funkcji 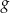 .
. 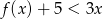 .
. 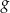 .
. 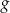 określona jest wzorem
określona jest wzorem 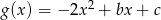 . Oblicz
. Oblicz 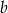 i
i  .
.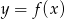 przesunięto o 2 jednostki do góry, następnie nowy wykres o 3 jednostki w lewo i otrzymano wykres funkcji
przesunięto o 2 jednostki do góry, następnie nowy wykres o 3 jednostki w lewo i otrzymano wykres funkcji 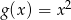 . Wyznacz wzór ogólny funkcji
. Wyznacz wzór ogólny funkcji 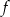 .
. 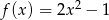 dla
dla 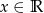 przez przesunięcie o wektor
przez przesunięcie o wektor ![→ u = [−1 ;2]](https://img.zadania.info/zad/7227565/HzadT2x.gif) .
. 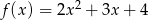 przesunięto o wektor
przesunięto o wektor ![→ v = [0,3]](https://img.zadania.info/zad/8939747/HzadT1x.gif) . Wyznacz wzór i narysuj wykres otrzymanej funkcji.
. Wyznacz wzór i narysuj wykres otrzymanej funkcji. 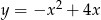 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→ u = [− 2,3]](https://img.zadania.info/zad/9470655/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy. 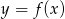 należą punkty
należą punkty 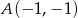 oraz
oraz 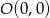 , który jest wierzchołkiem paraboli.
, który jest wierzchołkiem paraboli. 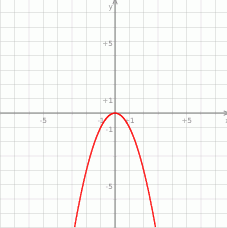
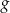 , której miejscami zerowymi są liczby 3 i 7.
, której miejscami zerowymi są liczby 3 i 7. 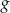 .
. 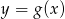 .
. 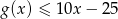 .
.