Dana jest prosta 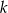 o równaniu parametrycznym
o równaniu parametrycznym 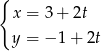 dla
dla 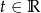 . Znajdź równanie parametryczne:
. Znajdź równanie parametryczne:
- prostej
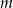 równoległej do prostej
równoległej do prostej 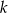 , przechodzącej przez punkt
, przechodzącej przez punkt 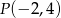 .
. - prostej
 prostopadłej do prostej
prostopadłej do prostej 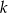 , przechodzącej przez punkt
, przechodzącej przez punkt 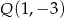 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dana jest prosta 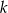 o równaniu parametrycznym
o równaniu parametrycznym 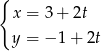 dla
dla 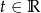 . Znajdź równanie parametryczne:
. Znajdź równanie parametryczne:
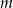 równoległej do prostej
równoległej do prostej 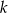 , przechodzącej przez punkt
, przechodzącej przez punkt 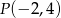 .
.  prostopadłej do prostej
prostopadłej do prostej 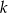 , przechodzącej przez punkt
, przechodzącej przez punkt 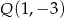 .
.Prosta 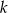 jest wykresem funkcji
jest wykresem funkcji 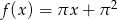 .
.
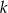 z wykresem funkcji
z wykresem funkcji 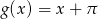 .
. 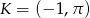 i równoległej do prostej
i równoległej do prostej 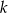 .
.Wyznacz równanie prostej równoległej do prostej 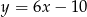 przechodzącej przez punkt
przechodzącej przez punkt 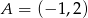 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 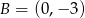 .
.
Napisz równanie prostej równoległej do prostej o równaniu 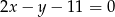 i przechodzącej przez punkt
i przechodzącej przez punkt 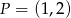 .
.
Zapisz równanie prostej przechodzącej przez punkt 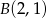 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 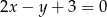 .
.
Wyznacz równanie prostej prostopadłej do prostej o równaniu 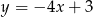 przechodzącej przez punkt
przechodzącej przez punkt 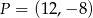 .
.
Wyznacz równanie prostej prostopadłej do prostej o równaniu 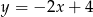 przecinającej oś
przecinającej oś 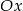 w punkcie o odciętej 4.
w punkcie o odciętej 4.
Zapisz równanie prostej przechodzącej przez punkt 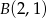 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 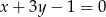 .
.
Wyznacz równanie prostej prostopadłej do prostej 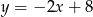 przechodzącej przez punkt
przechodzącej przez punkt 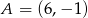 .
.
Dana jest funkcja 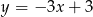 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 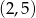 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
Dana jest funkcja 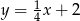 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 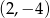 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
Prosta 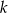 przechodzi przez punkty
przechodzi przez punkty 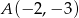 i
i 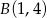 . Wyznacz równania prostej
. Wyznacz równania prostej 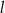 prostopadłej do
prostopadłej do 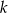 i prostej
i prostej 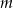 równoległej do
równoległej do 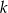 , jeżeli każda z nich przechodzi przez punkt
, jeżeli każda z nich przechodzi przez punkt 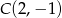 .
.
Wyznacz równanie prostej przechodzącej przez punkt 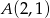 i tworzącej z prostą
i tworzącej z prostą 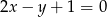 kąt o mierze
kąt o mierze 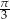 .
.
Zapisz równanie prostej przechodzącej przez punkt 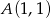 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 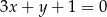 .
.
Zapisz równanie prostej przechodzącej przez punkt 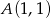 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 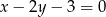 .
.
